| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
tricky
Forumaš(ica)

Pridružen/a: 01. 03. 2006. (23:22:39)
Postovi: (3D)16
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
tricky
Forumaš(ica)

Pridružen/a: 01. 03. 2006. (23:22:39)
Postovi: (3D)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
tricky
Forumaš(ica)

Pridružen/a: 01. 03. 2006. (23:22:39)
Postovi: (3D)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Nick Praskaton
Gost
|
|
| [Vrh] |
|
Madonna
Gost
|
 Postano: 22:13 pet, 23. 6. 2006 Naslov: Postano: 22:13 pet, 23. 6. 2006 Naslov: |
    |
|
|
[quote="Nick Praskaton"]Nisam baš najbolje skužio objašnjenje na papiru pa ako bi netko mogao pokazati da ovo vrijedi:
sin(1/x)<(2/x)*cos(1/x)[/quote]
Joj pa to ti je lagano, sve ti lijepo piše na papiru. Za koga sam ja to pisala, ha?? :roll: Prvo skoči, a onda reci Juuhuuuuu! :lol:
Pokažimo da je [latex]\sin\frac{1}{x}-\frac{2}{x}\cos\frac{1}{x}<0[/latex] za dovoljno velike x. (Ne treba nam za sve nego samo za dovoljno velike x, jer će onda niz od nekog mjesta nadalje padati.)
Možemo cijeli izraz podijeliti s [latex]\frac{1}{x}[/latex], jer je to ionako pozitivno za x>0.
[latex]\displaystyle\lim_{x\to+\infty}\frac{\sin\frac{1}{x}-\frac{2}{x}\cos\frac{1}{x}}{\frac{1}{x}}=1-2=-1<0[/latex]
Zato po definiciji limesa za x-eve veće od nekog broja vrijedi [latex]\displaystyle\frac{\sin\frac{1}{x}-\frac{2}{x}\cos\frac{1}{x}}{\frac{1}{x}}<0[/latex], tj. [latex]\displaystyle\sin\frac{1}{x}-\frac{2}{x}\cos\frac{1}{x}<0[/latex].
Nije to tako neuobičajeni argument, to s limesom.
_________
[img]http://www.virgin.net/music/wallpapers/images/madonna_thumb.jpg[/img]
| Nick Praskaton (napisa): | Nisam baš najbolje skužio objašnjenje na papiru pa ako bi netko mogao pokazati da ovo vrijedi:
sin(1/x)<(2/x)*cos(1/x) |
Joj pa to ti je lagano, sve ti lijepo piše na papiru. Za koga sam ja to pisala, ha??  Prvo skoči, a onda reci Juuhuuuuu! Prvo skoči, a onda reci Juuhuuuuu! 
Pokažimo da je 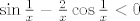 za dovoljno velike x. (Ne treba nam za sve nego samo za dovoljno velike x, jer će onda niz od nekog mjesta nadalje padati.) za dovoljno velike x. (Ne treba nam za sve nego samo za dovoljno velike x, jer će onda niz od nekog mjesta nadalje padati.)
Možemo cijeli izraz podijeliti s  , jer je to ionako pozitivno za x>0. , jer je to ionako pozitivno za x>0.
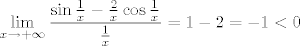
Zato po definiciji limesa za x-eve veće od nekog broja vrijedi 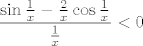 , tj. , tj. 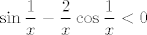 . .
Nije to tako neuobičajeni argument, to s limesom.
_________

|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 22:24 pet, 23. 6. 2006 Naslov: Postano: 22:24 pet, 23. 6. 2006 Naslov: |
    |
|
|
[quote="sun"]meni je kolokvij bas bio super, uopce nije bio tezak[/quote]
E, ja sam UMRO od straha kad sam vidio zadatke... ogroman broj (4, neki čak pod a i b), a ni nakon rješavanja nisam bio ništa sretniji. Pa ti asistenti (neki više od drugih) NISU NORMALNI. Znam da postoje neki standardi koje moramo zadovoljiti, ali previše je previše. Da mi kolegica nana nije riješila cijeli kolokvij dok je naša paziteljica izgledala odsutno, mislim da bih gotovo sigurno bodovi bili katastrofalni. Nadam se da nisam jedini koji je ovako iznenađen težinom kolokvija.
| sun (napisa): | | meni je kolokvij bas bio super, uopce nije bio tezak |
E, ja sam UMRO od straha kad sam vidio zadatke... ogroman broj (4, neki čak pod a i b), a ni nakon rješavanja nisam bio ništa sretniji. Pa ti asistenti (neki više od drugih) NISU NORMALNI. Znam da postoje neki standardi koje moramo zadovoljiti, ali previše je previše. Da mi kolegica nana nije riješila cijeli kolokvij dok je naša paziteljica izgledala odsutno, mislim da bih gotovo sigurno bodovi bili katastrofalni. Nadam se da nisam jedini koji je ovako iznenađen težinom kolokvija.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
|












