| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Perosito
Forumaš(ica)

Pridružen/a: 30. 01. 2004. (22:21:16)
Postovi: (7E)16
|
 Postano: 11:24 ned, 2. 7. 2006 Naslov: Sigma-algebra - neki zadaci Postano: 11:24 ned, 2. 7. 2006 Naslov: Sigma-algebra - neki zadaci |
    |
|
|
Evo, dva zadatka od onih dodatnih na netu iz Familije skupova, iako vidim da se ne pojavljuju na pismenom zadaci tog tipa, dobro je znati... :okgreen:
Zadatak 7: Neka je F sigma-algebra. Pokažite da F ne može imati točno 6 elemenata.
Ako netko može malo objasniti, jer ja ne znam ni otkud početi.
Zadatak 5: Neka je omega={1,2,3,4,5,6} i neka su A1={1}, A2={1,2}, A3={1,2,3}, A4={1,2,3,4} i A5={1,2,3,4,5}. Odredite najmanju sigma-algebru na omega koja sadrži skupove A1, A2, A3, A4 i A5.
E sad, ak može netko čisto ukratko pojasniti, nisam siguran dal mi je jasno.
Hvala unaprijed!
Evo, dva zadatka od onih dodatnih na netu iz Familije skupova, iako vidim da se ne pojavljuju na pismenom zadaci tog tipa, dobro je znati... 
Zadatak 7: Neka je F sigma-algebra. Pokažite da F ne može imati točno 6 elemenata.
Ako netko može malo objasniti, jer ja ne znam ni otkud početi.
Zadatak 5: Neka je omega={1,2,3,4,5,6} i neka su A1={1}, A2={1,2}, A3={1,2,3}, A4={1,2,3,4} i A5={1,2,3,4,5}. Odredite najmanju sigma-algebru na omega koja sadrži skupove A1, A2, A3, A4 i A5.
E sad, ak može netko čisto ukratko pojasniti, nisam siguran dal mi je jasno.
Hvala unaprijed!
_________________ Nije sve tako sivo... Kad imaš s nekim otić na pivo  |
|
| [Vrh] |
|
amimica
Forumaš(ica)

Pridružen/a: 14. 04. 2004. (15:40:42)
Postovi: (CA)16
|
 Postano: 11:53 ned, 2. 7. 2006 Naslov: Re: Sigma-algebra - neki zadaci Postano: 11:53 ned, 2. 7. 2006 Naslov: Re: Sigma-algebra - neki zadaci |
    |
|
|
[quote="Perosito"]
Zadatak 7: Neka je F sigma-algebra. Pokažite da F ne može imati točno 6 elemenata.
Ako netko može malo objasniti, jer ja ne znam ni otkud početi.
[/quote]
Uzmes skupove A i B koji nisu prazan skup ni citav omega i takve da im je presjek neprazan i da ni jedan nije podskup drugog. Tada su u sigma algebri
[latex]
\phi,\Omega,A,B,A^c,B^c,A\cap B,(A\cap B)^c
[/latex],
pa je u sigma algebri barem 8 elemenata elemenata.
Analogno se promatra u ostalim slucajevima...
[quote="Perosito"]
Zadatak 5: Neka je omega={1,2,3,4,5,6} i neka su A1={1}, A2={1,2}, A3={1,2,3}, A4={1,2,3,4} i A5={1,2,3,4,5}. Odredite najmanju sigma-algebru na omega koja sadrži skupove A1, A2, A3, A4 i A5.
E sad, ak može netko čisto ukratko pojasniti, nisam siguran dal mi je jasno.
Hvala unaprijed![/quote]
[latex]
A_2\backslash A_1=\{2\},\,A_3\backslash A_2=\{3\},\,A_4\backslash A_3=\{4\},A_5\backslash A_4=\{5\},\Omega\backslash A_5=\{6\}
[/latex]
pa je najmanja sigma algebra zapravo partitivni skup od omega.
| Perosito (napisa): |
Zadatak 7: Neka je F sigma-algebra. Pokažite da F ne može imati točno 6 elemenata.
Ako netko može malo objasniti, jer ja ne znam ni otkud početi.
|
Uzmes skupove A i B koji nisu prazan skup ni citav omega i takve da im je presjek neprazan i da ni jedan nije podskup drugog. Tada su u sigma algebri
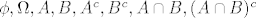 , ,
pa je u sigma algebri barem 8 elemenata elemenata.
Analogno se promatra u ostalim slucajevima...
| Perosito (napisa): |
Zadatak 5: Neka je omega={1,2,3,4,5,6} i neka su A1={1}, A2={1,2}, A3={1,2,3}, A4={1,2,3,4} i A5={1,2,3,4,5}. Odredite najmanju sigma-algebru na omega koja sadrži skupove A1, A2, A3, A4 i A5.
E sad, ak može netko čisto ukratko pojasniti, nisam siguran dal mi je jasno.
Hvala unaprijed! |
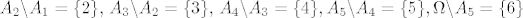
pa je najmanja sigma algebra zapravo partitivni skup od omega.
|
|
| [Vrh] |
|
kreda
Forumaš(ica)
Pridružen/a: 21. 08. 2005. (23:07:55)
Postovi: (44)16
|
 Postano: 14:58 ned, 2. 7. 2006 Naslov: Postano: 14:58 ned, 2. 7. 2006 Naslov: |
    |
|
|
Ja imam pitanje također u vezi sigma algebre...To je 2. zadatak s 1. kolokvija.
Omega=[0,1] i F sigma algebra na omega koja sadrži sve segmente [a,b], 0<=a<b<=1, i neka je P:F-> [0,1] vj.definirana na sigma-algebri F s P([a,b])= b-a.
a) Definiramo niz događaja An=[0, 1/n]. Izračunajte limsupAn i P(limsupAn).
TO je pretpostavljam jednako nula, ali kako da to izracunam?
b) Nađite tri (različita) događaja iz F koja su nezavisna s [0, 1/2].
Jel uopce postoje takvi događaji? Meni se čini da ne postoje...
Molim vas odgovorite :roll:
Ja imam pitanje također u vezi sigma algebre...To je 2. zadatak s 1. kolokvija.
Omega=[0,1] i F sigma algebra na omega koja sadrži sve segmente [a,b], 0⇐a<b⇐1, i neka je P:F→ [0,1] vj.definirana na sigma-algebri F s P([a,b])= b-a.
a) Definiramo niz događaja An=[0, 1/n]. Izračunajte limsupAn i P(limsupAn).
TO je pretpostavljam jednako nula, ali kako da to izracunam?
b) Nađite tri (različita) događaja iz F koja su nezavisna s [0, 1/2].
Jel uopce postoje takvi događaji? Meni se čini da ne postoje...
Molim vas odgovorite 
|
|
| [Vrh] |
|
hermione
Forumaš(ica)


Pridružen/a: 23. 09. 2003. (10:50:57)
Postovi: (152)16
Spol: 
Sarma: -
|
 Postano: 15:07 ned, 2. 7. 2006 Naslov: Postano: 15:07 ned, 2. 7. 2006 Naslov: |
    |
|
|
[quote="kreda"]Ja imam pitanje također u vezi sigma algebre...To je 2. zadatak s 1. kolokvija.
Omega=[0,1] i F sigma algebra na omega koja sadrži sve segmente [a,b], 0<=a<b<=1, i neka je P:F-> [0,1] vj.definirana na sigma-algebri F s P([a,b])= b-a.
a) Definiramo niz događaja An=[0, 1/n]. Izračunajte limsupAn i P(limsupAn).
TO je pretpostavljam jednako nula, ali kako da to izracunam?
b) Nađite tri (različita) događaja iz F koja su nezavisna s [0, 1/2].
Jel uopce postoje takvi događaji? Meni se čini da ne postoje...
Molim vas odgovorite :roll:[/quote]
Baci oko na ovo http://web.math.hr/nastava/uvis/files/r240206.pdf
| kreda (napisa): | Ja imam pitanje također u vezi sigma algebre...To je 2. zadatak s 1. kolokvija.
Omega=[0,1] i F sigma algebra na omega koja sadrži sve segmente [a,b], 0⇐a<b⇐1, i neka je P:F→ [0,1] vj.definirana na sigma-algebri F s P([a,b])= b-a.
a) Definiramo niz događaja An=[0, 1/n]. Izračunajte limsupAn i P(limsupAn).
TO je pretpostavljam jednako nula, ali kako da to izracunam?
b) Nađite tri (različita) događaja iz F koja su nezavisna s [0, 1/2].
Jel uopce postoje takvi događaji? Meni se čini da ne postoje...
Molim vas odgovorite  |
Baci oko na ovo http://web.math.hr/nastava/uvis/files/r240206.pdf
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kreda
Forumaš(ica)
Pridružen/a: 21. 08. 2005. (23:07:55)
Postovi: (44)16
|
|
| [Vrh] |
|
amimica
Forumaš(ica)

Pridružen/a: 14. 04. 2004. (15:40:42)
Postovi: (CA)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|





