| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 12:51 sub, 4. 2. 2006 Naslov: dva integrala Postano: 12:51 sub, 4. 2. 2006 Naslov: dva integrala |
    |
|
|
površina skupa koji je dio kvadrata s vrhovima (0,1), (1,0), (2,1), (1,2) koji leži između hiperbola xy=1 i xy=2
volumen tijela ograničenog sa x^2 + y^2/4 + z^2/9=1 i
x^2 + y^2/4=z/9
zapravo mi samo treba ideja za zamjenu varijabli budući mi se ti presjeci ne čine "lijepima" pa standardne zamjene ne mogu koristiti
površina skupa koji je dio kvadrata s vrhovima (0,1), (1,0), (2,1), (1,2) koji leži između hiperbola xy=1 i xy=2
volumen tijela ograničenog sa x^2 + y^2/4 + z^2/9=1 i
x^2 + y^2/4=z/9
zapravo mi samo treba ideja za zamjenu varijabli budući mi se ti presjeci ne čine "lijepima" pa standardne zamjene ne mogu koristiti
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 13:57 sub, 4. 2. 2006 Naslov: Re: dva integrala Postano: 13:57 sub, 4. 2. 2006 Naslov: Re: dva integrala |
    |
|
|
[quote="Anonymous"]površina skupa koji je dio kvadrata s vrhovima (0,1), (1,0), (2,1), (1,2) koji leži između hiperbola xy=1 i xy=2
volumen tijela ograničenog sa x^2 + y^2/4 + z^2/9=1 i
x^2 + y^2/4=z/9
zapravo mi samo treba ideja za zamjenu varijabli budući mi se ti presjeci ne čine "lijepima" pa standardne zamjene ne mogu koristiti[/quote]
Za prvi bih probao ovakvu supstituciju
[latex]u = y - x \in \left[-1, 1\right] \\
v = xy \in \left[ 1, 2 \right] \\
\psi (x,y) = (y - x, xy) \Rightarrow J(\psi) = -x - y \Rightarrow J(\phi) = \frac{1}{J(\psi)} = -\frac{1}{x + y}=-\frac{1}{\sqrt{u^2 + 4v}}[/latex]
Pa se sad to valjda da integrirat
| Anonymous (napisa): | površina skupa koji je dio kvadrata s vrhovima (0,1), (1,0), (2,1), (1,2) koji leži između hiperbola xy=1 i xy=2
volumen tijela ograničenog sa x^2 + y^2/4 + z^2/9=1 i
x^2 + y^2/4=z/9
zapravo mi samo treba ideja za zamjenu varijabli budući mi se ti presjeci ne čine "lijepima" pa standardne zamjene ne mogu koristiti |
Za prvi bih probao ovakvu supstituciju
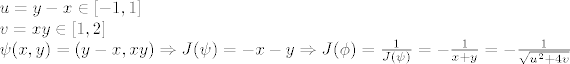
Pa se sad to valjda da integrirat
_________________
Bri
|
|
| [Vrh] |
|
mea
Forumaš(ica)

Pridružen/a: 10. 12. 2002. (13:22:34)
Postovi: (1F0)16
|
 Postano: 18:24 sub, 4. 2. 2006 Naslov: Re: dva integrala Postano: 18:24 sub, 4. 2. 2006 Naslov: Re: dva integrala |
    |
|
|
[quote="Anonymous"]volumen tijela ograničenog sa x^2 + y^2/4 + z^2/9=1 i x^2 + y^2/4=z/9[/quote]
Eliptične koordinate u x-y ravnini, tj
(x,y,z)-->(r cos t, 2r sin t, z).
| Anonymous (napisa): | | volumen tijela ograničenog sa x^2 + y^2/4 + z^2/9=1 i x^2 + y^2/4=z/9 |
Eliptične koordinate u x-y ravnini, tj
(x,y,z)→(r cos t, 2r sin t, z).
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
mea
Forumaš(ica)

Pridružen/a: 10. 12. 2002. (13:22:34)
Postovi: (1F0)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
akki
Forumaš(ica)


Pridružen/a: 28. 09. 2004. (14:55:35)
Postovi: (88)16
|
 Postano: 20:52 uto, 4. 7. 2006 Naslov: Postano: 20:52 uto, 4. 7. 2006 Naslov: |
    |
|
|
[quote="mea"][quote="Anonymous"]z ide od -sqrt((1-r^2)/9) do sqrt((1-r^2)/9) ?[/quote]
Ne, to bi značilo (uz odgovarajuće granice za r i t) po cijelom elipsoidu.
z treba ići od elipsoida do paraboloida. Skiciraj r^2+z^2/9=1 i r^2=z/9, pa zaključi. Granica za r je ružna...[/quote]
Da li je dobro ovako?
r iz (0,1)
t iz (0,2pi)
z iz (sqrt(2)*r/3,sqrt(1-2r^2)/3)
:?
| mea (napisa): | | Anonymous (napisa): | | z ide od -sqrt((1-r^2)/9) do sqrt((1-r^2)/9) ? |
Ne, to bi značilo (uz odgovarajuće granice za r i t) po cijelom elipsoidu.
z treba ići od elipsoida do paraboloida. Skiciraj r^2+z^2/9=1 i r^2=z/9, pa zaključi. Granica za r je ružna... |
Da li je dobro ovako?
r iz (0,1)
t iz (0,2pi)
z iz (sqrt(2)*r/3,sqrt(1-2r^2)/3)

_________________ 
 Kad jednom probas letjeti
hodati ces zemljom, s pogledom prema gore,
tamo gdje si bio i kamo se čezneš vratiti....
  |
|
| [Vrh] |
|
Gost
|
 Postano: 23:44 uto, 4. 7. 2006 Naslov: Postano: 23:44 uto, 4. 7. 2006 Naslov: |
    |
|
|
Dakle kako se meni vidi treba izraziti z preko r pa dobivamo situaciju u R^2 i onda otuda dobiti granicu za z.
Ja sam išao računati presjek elipse (z^2/9 + r^2=1) i parabole (r^2=z/9); dobio kvadratnu jednađbu po z rješio i dobio z=-1+sqrt(57)/2
kao z-koordinatu presjeka.Sada računam I1 kao volumen elipsoida od donjeg kraja do točke presjeka i I2 kao volumen paraboloida od početka do točke presjeka i traženi integral je I=I1-I2
I1:fi iz [0,2pi]
r iz [0,1]
z iz [3sqrt(1-r^2), -1+sqrt(57)/2]
I2:fi iz [0.2pi]
r iz [0,1]
z iz [9r^2, -1+sqrt(57)/2]
Dakle kako se meni vidi treba izraziti z preko r pa dobivamo situaciju u R^2 i onda otuda dobiti granicu za z.
Ja sam išao računati presjek elipse (z^2/9 + r^2=1) i parabole (r^2=z/9); dobio kvadratnu jednađbu po z rješio i dobio z=-1+sqrt(57)/2
kao z-koordinatu presjeka.Sada računam I1 kao volumen elipsoida od donjeg kraja do točke presjeka i I2 kao volumen paraboloida od početka do točke presjeka i traženi integral je I=I1-I2
I1:fi iz [0,2pi]
r iz [0,1]
z iz [3sqrt(1-r^2), -1+sqrt(57)/2]
I2:fi iz [0.2pi]
r iz [0,1]
z iz [9r^2, -1+sqrt(57)/2]
|
|
| [Vrh] |
|
|





