| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 20:47 sri, 8. 6. 2005 Naslov: par zadataka |
    |
|
|
Znam da nije malo zadataka, ali ako mi moze netko dati samo ideju kako da pocnem bio bi zahvalan.
1. U kutiji se nalazi 8 novcanica od 20 KN, 4 novcanice od 10 KN i 3 novcanice po 5KN. Na slucajan nacin se se iz kutije uzimaju 6 novcanica. Odredite vjerojatnost da vrijednost izvucenih novcanica bude najvise 100 KN.
2. Mile i Ana se dogovore za sastanak na Trgu kod sata. Njihovi dolasci su slucajni vremenski trenutci izmedu 20h i 21h. Ako Mile prvi dode kod sata, on ce pricekati pola sata, dok ce Ana, ako prva dode, cekati samo 10 min. Odredite vjerojatnost da se Mile i Ana sretnu.
3.Imamo dvije kutije i 50 kuglica. 25 kuglica je bijelo, 25 crno. Rasporedite tih 50 kuglica u dvije kutije tako da je vjerojatnost izvlacenja 1 bijele kuglice iz jedne od kutija najveca moguca, pri cemu nema restrikcija na broj rasporedjenih kuglica i vjerojatnosti odabira kutije su jednako vjerojatne. Objasnite svoj postupak.
4. Unutar duzine duljine 11 slucajno su izabrane 2 tocke koje zadanu duzinu dijele na 3 dijela. kolika je vjerojatnost da je duljina najkraceg dijela od njih veca od 3 ?
Znam da nije malo zadataka, ali ako mi moze netko dati samo ideju kako da pocnem bio bi zahvalan.
1. U kutiji se nalazi 8 novcanica od 20 KN, 4 novcanice od 10 KN i 3 novcanice po 5KN. Na slucajan nacin se se iz kutije uzimaju 6 novcanica. Odredite vjerojatnost da vrijednost izvucenih novcanica bude najvise 100 KN.
2. Mile i Ana se dogovore za sastanak na Trgu kod sata. Njihovi dolasci su slucajni vremenski trenutci izmedu 20h i 21h. Ako Mile prvi dode kod sata, on ce pricekati pola sata, dok ce Ana, ako prva dode, cekati samo 10 min. Odredite vjerojatnost da se Mile i Ana sretnu.
3.Imamo dvije kutije i 50 kuglica. 25 kuglica je bijelo, 25 crno. Rasporedite tih 50 kuglica u dvije kutije tako da je vjerojatnost izvlacenja 1 bijele kuglice iz jedne od kutija najveca moguca, pri cemu nema restrikcija na broj rasporedjenih kuglica i vjerojatnosti odabira kutije su jednako vjerojatne. Objasnite svoj postupak.
4. Unutar duzine duljine 11 slucajno su izabrane 2 tocke koje zadanu duzinu dijele na 3 dijela. kolika je vjerojatnost da je duljina najkraceg dijela od njih veca od 3 ?
|
|
| [Vrh] |
|
Boris Davidovič
Forumaš(ica)
Pridružen/a: 08. 01. 2004. (23:05:18)
Postovi: (3C)16
|
| Postano: 7:05 čet, 9. 6. 2005 Naslov: |
|
|
|
1.Izračunaj vjerojatnost komplementa. Naime nema baš tako puno slučajeva da suma bude veća od 100.
2.Geometrijska vjerojatnost, nacrtaj kvadrat i odgovarajuće pravce(npr. x os ti je dolazak Milana, a y dolazak Ane).
3.U prvu kutiju staviš jednu bijelu, u drugu sve ostale. Onda uzmeš proizvoljan slučaj(u prvoj kutiji a1 bijelih i b1 crnih, u drugoj a2,b2) i računaš vjerojatnost izvlačenja bijele po formuli potpune vjerojatnosti. Pokaže se da je ono najbolji odabir(njegova vjerojatnost je 1/2+1/2*(24/49)).
4.To možemo modelirati ovako: biramo x,y iz [0,11]. Bso x<y(kasnije rezultat množimo s 2, jer je drugo jednako vjerojatno). Nacrtaj si sliku. Prvi dio (do x) neka je k, od x do y l, od y do 11 m. Očito k=x, l=y-x, m=11-y. Uvjeti su k,l,m>=3. Nacrtaj i izračunaj vjerojatnost. Na kraju množi s dva.
1.Izračunaj vjerojatnost komplementa. Naime nema baš tako puno slučajeva da suma bude veća od 100.
2.Geometrijska vjerojatnost, nacrtaj kvadrat i odgovarajuće pravce(npr. x os ti je dolazak Milana, a y dolazak Ane).
3.U prvu kutiju staviš jednu bijelu, u drugu sve ostale. Onda uzmeš proizvoljan slučaj(u prvoj kutiji a1 bijelih i b1 crnih, u drugoj a2,b2) i računaš vjerojatnost izvlačenja bijele po formuli potpune vjerojatnosti. Pokaže se da je ono najbolji odabir(njegova vjerojatnost je 1/2+1/2*(24/49)).
4.To možemo modelirati ovako: biramo x,y iz [0,11]. Bso x<y(kasnije rezultat množimo s 2, jer je drugo jednako vjerojatno). Nacrtaj si sliku. Prvi dio (do x) neka je k, od x do y l, od y do 11 m. Očito k=x, l=y-x, m=11-y. Uvjeti su k,l,m>=3. Nacrtaj i izračunaj vjerojatnost. Na kraju množi s dva.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
hermione
Forumaš(ica)
Pridružen/a: 23. 09. 2003. (10:50:57)
Postovi: (152)16
Spol: 
Sarma: -
|
| Postano: 23:41 uto, 20. 6. 2006 Naslov: |
|
|
|
[quote="Anonymous"]Moze li netko malo pojasnit ovaj prvi zadatak.ako trazimo komplement imamo onda 2 slucaja,jedan da smo izabrali 5 novcanica od 20 i jednu od 10,i drugi slucaj da smo izabrali 5 novcanica od 20 i jednui od 5.
Kad izracunam te dvije vjerojatnosti sta onda s njima?jel se zbrajaju te dvije vjerojatnosti i onda 1i taj zbroj ili?[/quote]
Dakle, cilj nam je naci sve one slucajeve da suma
novcanica bude barem100. To mozemo napraviti na 3
nacina:[latex]5\times20+1\times10, 4\times20+2\times10\, i\,
5\times20+1\times5.
[/latex]
Trazena vjerojatnost je :
[latex]\frac{{8\choose5} {4\choose1}+{8\choose4}{4\choose2}+{8\choose5}{3\choose1}}{{15\choose6}}
[/latex]
| Anonymous (napisa): | Moze li netko malo pojasnit ovaj prvi zadatak.ako trazimo komplement imamo onda 2 slucaja,jedan da smo izabrali 5 novcanica od 20 i jednu od 10,i drugi slucaj da smo izabrali 5 novcanica od 20 i jednui od 5.
Kad izracunam te dvije vjerojatnosti sta onda s njima?jel se zbrajaju te dvije vjerojatnosti i onda 1i taj zbroj ili? |
Dakle, cilj nam je naci sve one slucajeve da suma
novcanica bude barem100. To mozemo napraviti na 3
nacina: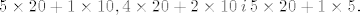
Trazena vjerojatnost je :
|
|
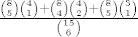
| [Vrh] |
|
Gost
|
| Postano: 23:56 uto, 20. 6. 2006 Naslov: |
|
|
|
[quote="hermione"][quote="Anonymous"]Moze li netko malo pojasnit ovaj prvi zadatak.ako trazimo komplement imamo onda 2 slucaja,jedan da smo izabrali 5 novcanica od 20 i jednu od 10,i drugi slucaj da smo izabrali 5 novcanica od 20 i jednui od 5.
Kad izracunam te dvije vjerojatnosti sta onda s njima?jel se zbrajaju te dvije vjerojatnosti i onda 1i taj zbroj ili?[/quote]
Dakle, cilj nam je naci sve one slucajeve da suma
novcanica bude barem100. To mozemo napraviti na 3
nacina:[latex]5\times20+1\times10, 4\times20+2\times10\, i\,
5\times20+1\times5.
[/latex]
Trazena vjerojatnost je :
[latex]\frac{{8\choose5} {4\choose1}+{8\choose4}{4\choose2}+{8\choose5}{3\choose1}}{{15\choose6}}
[/latex][/quote]Puno hvala :P :D
| hermione (napisa): | | Anonymous (napisa): | Moze li netko malo pojasnit ovaj prvi zadatak.ako trazimo komplement imamo onda 2 slucaja,jedan da smo izabrali 5 novcanica od 20 i jednu od 10,i drugi slucaj da smo izabrali 5 novcanica od 20 i jednui od 5.
Kad izracunam te dvije vjerojatnosti sta onda s njima?jel se zbrajaju te dvije vjerojatnosti i onda 1i taj zbroj ili? |
Dakle, cilj nam je naci sve one slucajeve da suma
novcanica bude barem100. To mozemo napraviti na 3
nacina: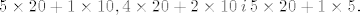
Trazena vjerojatnost je :
|
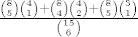Puno hvala  
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: 
Lokacija: /sbin/init
|
| Postano: 11:27 uto, 18. 7. 2006 Naslov: |
|
|
|
[quote="Anonymous"]Moze li netko rjesiti ovaj zadatak:
A, B i C igraju igru po sljedecim pravilima: u svakoj partiji sudjeluju 2 igraca, onaj koji izgubi partiju ustupa mjesto trecem igracu. Igra staje kada jedan od igraca pobjedi u dvije uzastopne partije. Prvu partiju igraju B i C. Pobjednik dobiva onoliko KN koliko je ukupno odigrano partija do trenutka pobjede. Vjerojatnost pobjede u partiji za svakog igraca je 0.5. Odredite vjerojatnost da B osvoji 8KN, te ocekivani dobitak za C.[/quote]
Ovo je vec rijeseno. :roll: Upotrijebi [url=http://degiorgi.math.hr/forum/search.php]trazilicu[/url]. 8)
| Anonymous (napisa): | Moze li netko rjesiti ovaj zadatak:
A, B i C igraju igru po sljedecim pravilima: u svakoj partiji sudjeluju 2 igraca, onaj koji izgubi partiju ustupa mjesto trecem igracu. Igra staje kada jedan od igraca pobjedi u dvije uzastopne partije. Prvu partiju igraju B i C. Pobjednik dobiva onoliko KN koliko je ukupno odigrano partija do trenutka pobjede. Vjerojatnost pobjede u partiji za svakog igraca je 0.5. Odredite vjerojatnost da B osvoji 8KN, te ocekivani dobitak za C. |
Ovo je vec rijeseno.  Upotrijebi trazilicu. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
|
