|
[quote="Crazylamb1"]Zadatak je da se nadje zapremina koju isjecaju oblasti:
1. z=x^2 + y^2, z=x+y[/quote]
[latex]\int\limits_{\{(x,y):x^2+y^2\leq x+y\}}(-x^2-y^2+x+y)\,dx\,dy=\\
=\int\limits_{\{(x,y):(x-1/2)^2+(y-1/2)^2\leq 1/2\}}(-(x-1/2)^2-(y-1/2)^2+1/2)\,dx\,dy=\\
=\int_0^{1/\sqrt{2}}\int_0^{2\pi}(-r^2+1/2)r\,dr\,d\varphi=\\
=2\pi\int_0^{1/\sqrt{2}}(-r^2+1/2)r\,dr[/latex]
Ovdje smo presli na polarne koordinate:
[latex]x=1/2+r\cos\varphi, \ y=1/2+r\sin\varphi[/latex]
[quote="Crazylamb1"]3. x^2 + y^2 = a^2, a>0, x + y = +/-a, x - y = +/-a[/quote]
Povrsina kvadrata s vrhovima (a,0), (0,a), (-a,0), (0,-a) = 2a^2
[quote="Crazylamb1"]4. x^2 + y^2 + (z^2)/4 <= 6, x^2 + y^2 - z^2 <= 1 (*koristim "<=" da znaci manje ili jednako)[/quote]
[latex]\pi\int_{-2}^2 (z^2+1)\,dz+\pi\int_2^{\sqrt{24}}(6-\frac{z^2}{4})dz+\\
+\pi\int_{-\sqrt{24}}^{-2}(6-\frac{z^2}{4})dz[/latex]
[quote="Crazylamb1"]5. x^2 + y^2 = 2x, x^2 + y^2 = 2y, z=0, z=x+2y[/quote]
Prve dvije jednadzbe predstavljaju cilindricne plohe nad kruznicama. Neka je S njihovo zajendnicko podrucje u xy-ravnini.
[latex]\int_S (x+2y)\,dx\,dy[/latex]
Ovo je zbog simetrije od S obzirom na y=x jednako:
[latex]3\int_S x\,dx\,dy=\\
=3\int_0^1 x(\sqrt{2x-x^2}+\sqrt{1-x^2}-1)\,dx[/latex]
[quote="Crazylamb1"]1. Naci povrsinu ogranicenu sa:
(x^2 + y^2)^2 = 2(a^2)(x^2 - y^2), x^2 + y^2 = 2ax[/quote]
Prelazimo na polarne koordinate [latex](r,\varphi)[/latex]:
[latex]x=a+ar\cos\varphi, \ y=ar\sin\varphi[/latex]
Krivulje sada imaju jednadzbe:
[latex](1+r^2+2r\cos\varphi)^2=2(1+r^2\cos2\varphi+2r\cos\varphi)[/latex] i [latex]r=1[/latex]
Prva jednadzba se moze jednostavnije zapisati
[latex]r^2(r^2+4r\cos\varphi+4)=1[/latex]
i lako se vidi da ta krivulja cijela pripada krugu r<=1, tj. lezi unutar ili na rubu kruznice r=1.
[quote="Crazylamb1"]Sto je to elipsoid? Bolje receno, kako glasi jednacina elipsoida? Cesto vidim da se trazi da se nadje zadani trostruki integral po unutrasnjosti elipsoida.[/quote]
[latex]\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}<=1[/latex]
Imas ga npr. u 4. zadatku.
[quote="Crazylamb1"]Unaprijed hvala za svaku i bilo kakvu pomoc, jer znam da pitam mnogo! :)[/quote]
Ma nije puno. Mogao si komotno prepisati cijelu zbirku.
[color=blue]___ ogranak Zavoda u emigraciji ___[/color]
| Crazylamb1 (napisa): | Zadatak je da se nadje zapremina koju isjecaju oblasti:
1. z=x^2 + y^2, z=x+y |
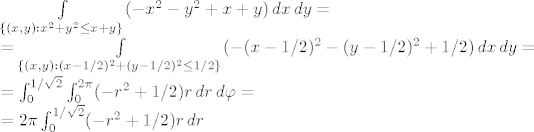
Ovdje smo presli na polarne koordinate:
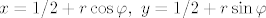
| Crazylamb1 (napisa): | | 3. x^2 + y^2 = a^2, a>0, x + y = +/-a, x - y = +/-a |
Povrsina kvadrata s vrhovima (a,0), (0,a), (-a,0), (0,-a) = 2a^2
| Crazylamb1 (napisa): | | 4. x^2 + y^2 + (z^2)/4 ⇐ 6, x^2 + y^2 - z^2 ⇐ 1 (*koristim "⇐" da znaci manje ili jednako) |
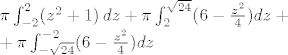
| Crazylamb1 (napisa): | | 5. x^2 + y^2 = 2x, x^2 + y^2 = 2y, z=0, z=x+2y |
Prve dvije jednadzbe predstavljaju cilindricne plohe nad kruznicama. Neka je S njihovo zajendnicko podrucje u xy-ravnini.
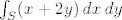
Ovo je zbog simetrije od S obzirom na y=x jednako:
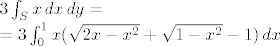
| Crazylamb1 (napisa): | 1. Naci povrsinu ogranicenu sa:
(x^2 + y^2)^2 = 2(a^2)(x^2 - y^2), x^2 + y^2 = 2ax |
Prelazimo na polarne koordinate 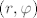 : :
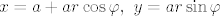
Krivulje sada imaju jednadzbe:
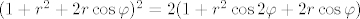 i i 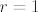
Prva jednadzba se moze jednostavnije zapisati
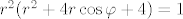
i lako se vidi da ta krivulja cijela pripada krugu r⇐1, tj. lezi unutar ili na rubu kruznice r=1.
| Crazylamb1 (napisa): | | Sto je to elipsoid? Bolje receno, kako glasi jednacina elipsoida? Cesto vidim da se trazi da se nadje zadani trostruki integral po unutrasnjosti elipsoida. |
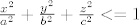
Imas ga npr. u 4. zadatku.
| Crazylamb1 (napisa): | Unaprijed hvala za svaku i bilo kakvu pomoc, jer znam da pitam mnogo!  |
Ma nije puno. Mogao si komotno prepisati cijelu zbirku.
___ ogranak Zavoda u emigraciji ___
_________________  |






