|
Uh, pa malo teže ti je sad samo na primjerima objasniti kako bi se trebalo rješavati.
Prvo i osnovno što radiš kod ovih zadataka je da nađeš nultočke karakterističnog polinoma, odnosno za zadatak 1 nultočke polinoma:
[latex]\lambda^2-6\lambda+9=0[/latex], a za drugi zadatak:
[latex]\lambda^2-3\lambda+2=0[/latex].
Prvi zadatak je linearna jednadžba n-tog reda s konstantnim koeficijentima i ona se nalazi tako da se nađe matrica Wronskoga i onda se rješava sustav.
Prvo trebaš rješiti homogenu jednadžbu,tj.
y''-6y'+9y=0,
a konačno rješenje će biti oblika y=yh+yp gdje je yh oznaka za rješenje homogene jednadžbe, a yp oznaka za jedno partikularno rješenje jednadžbe p.
Rješenja homogene jednadžbe se nalaze preko karakterističnog polinoma,tj.
[latex]\lambda^2-6\lambda+9=(\lambda - 3)^2=0 \\
\lambda_1=3 \\
\lambda_2=-3[/latex]
Za prvu nultočku rješenje je [latex]e^{3x}[/latex], a za drugu nultočku je rješenje [latex]e^{-3x}[/latex], tj. homogeno rješenje je oblika:
[latex]y_h=C_1e^{3x}+C_2e^{-3x}[/latex]
Sada trebaš naći partikularno rješenje, tj. nehomogeno rješenje. Na C1 i C2 više ne gledaš kao na konstante nego kao na funkcije, tj. ako je rješenje homogene jednadžbe dano sa:
[latex]y_h=C_1y_1+C_2y_2+\dots + C_ny_n[/latex], onda opće rješenje nehomogene tražimo u obliku:
[latex]y_p=C_1(x)y_1+C_2(x)y_2+\dots + C_n(x)y_n[/latex].
Nama n ide do 2 i da bi našli takve funkcije postavljamo uvjete:
[latex]
C_1' y_1 + C_2' y_2+ \dots + C_n' y_n=0 \quad \textrm{Uoci derivacije na C!!!}\\
C_1' y_1' + C_2' y_2'+ \dots + C_n' y_n'=0 \quad \textrm{Uoci derivacije na y!!!}
[/latex]
[latex]
\vdots \\
C_1' y_1^{(n-2)} + C_2' y_2^{(n-2)}+ \dots + C_n' y_n^{(n-2)}=0
[/latex]
I vrijedi još:
[latex]C_1' y_1^{(n-1)} + C_2' y_2^{(n-1)}+ \dots + C_n' y_n^{(n-1)}=f(x)
[/latex]
gdje je f(x)=2x^2-x+3
Ovaj gornji sustav zapravo opisuje matricu Wronskog što sam spomenuo, no nije sada bitno. Trenutno za ovaj zadatak je
[latex]C_1y_1=C_1(x)e^{3x} \\
C_2y_2=C_2(x)e^{-3x}[/latex]
I rjesavaš sustav (n=2)
[latex]
C_1' y_1 + C_2' y_2=0 \\
C_1' y_1' + C_2' y_2'=f(x)
[/latex]
Kada ga riješiš, trebala bi dobiti dvije funkcije C1(x) i C2(x), tj. njihove derivacije.
Kada ih dobiješ, integriraš ih da dobiješ funkcije C1(x) i C2(x) (nesmiješ zaboraviti konstante integriranja za te dvije funkcije) i moraš ih vratiti nazad u opće rješenje nehomogene jednadžbe, tj.
[latex]y_p=C_1(x)y_1+C_2(x)y_2+\dots + C_n(x)y_n[/latex]
I nakraju, konačno rješenje je [latex]y=y_h+y_p[/latex] gdje je yh homogeno rješenje (sa svojim neodređenim konstantama C1 i C2) i yp nehomogeno rješenje.
Drugi zadatak malo kasnije (mora se rješavati metodom neodređenih koeficijenata).
Uh, pa malo teže ti je sad samo na primjerima objasniti kako bi se trebalo rješavati.
Prvo i osnovno što radiš kod ovih zadataka je da nađeš nultočke karakterističnog polinoma, odnosno za zadatak 1 nultočke polinoma:
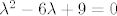 , a za drugi zadatak: , a za drugi zadatak:
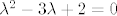 . .
Prvi zadatak je linearna jednadžba n-tog reda s konstantnim koeficijentima i ona se nalazi tako da se nađe matrica Wronskoga i onda se rješava sustav.
Prvo trebaš rješiti homogenu jednadžbu,tj.
y''-6y'+9y=0,
a konačno rješenje će biti oblika y=yh+yp gdje je yh oznaka za rješenje homogene jednadžbe, a yp oznaka za jedno partikularno rješenje jednadžbe p.
Rješenja homogene jednadžbe se nalaze preko karakterističnog polinoma,tj.
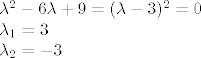
Za prvu nultočku rješenje je 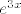 , a za drugu nultočku je rješenje , a za drugu nultočku je rješenje 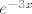 , tj. homogeno rješenje je oblika: , tj. homogeno rješenje je oblika:
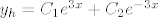
Sada trebaš naći partikularno rješenje, tj. nehomogeno rješenje. Na C1 i C2 više ne gledaš kao na konstante nego kao na funkcije, tj. ako je rješenje homogene jednadžbe dano sa:
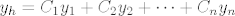 , onda opće rješenje nehomogene tražimo u obliku: , onda opće rješenje nehomogene tražimo u obliku:
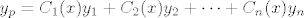 . .
Nama n ide do 2 i da bi našli takve funkcije postavljamo uvjete:

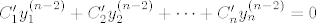
I vrijedi još:
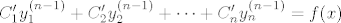
gdje je f(x)=2x^2-x+3
Ovaj gornji sustav zapravo opisuje matricu Wronskog što sam spomenuo, no nije sada bitno. Trenutno za ovaj zadatak je
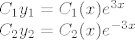
I rjesavaš sustav (n=2)
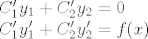
Kada ga riješiš, trebala bi dobiti dvije funkcije C1(x) i C2(x), tj. njihove derivacije.
Kada ih dobiješ, integriraš ih da dobiješ funkcije C1(x) i C2(x) (nesmiješ zaboraviti konstante integriranja za te dvije funkcije) i moraš ih vratiti nazad u opće rješenje nehomogene jednadžbe, tj.
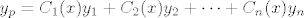
I nakraju, konačno rješenje je 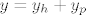 gdje je yh homogeno rješenje (sa svojim neodređenim konstantama C1 i C2) i yp nehomogeno rješenje. gdje je yh homogeno rješenje (sa svojim neodređenim konstantama C1 i C2) i yp nehomogeno rješenje.
Drugi zadatak malo kasnije (mora se rješavati metodom neodređenih koeficijenata).
_________________
The Dude Abides
|




