| Prethodna tema :: Sljedeća tema |
| Kako ocjenjujete težinu zadataka za vježbu? |
| Ne razumijem što zadaci hoće. |
|
0% |
[ 0 ] |
| Shvaćam zadatak, ali ne znam odakle početi. |
|
10% |
[ 1 ] |
| Okvirno znam što napraviti, ali ne uspijevam iskodirati. |
|
30% |
[ 3 ] |
| Vrlo teško, ali ipak dobivam program koji donekle radi. |
|
10% |
[ 1 ] |
| Treba truda ali mogu ih riješiti u razumnom vremenu. |
|
40% |
[ 4 ] |
| Teški trivić, hoću prave stvari! |
|
0% |
[ 0 ] |
| Ma kakvi zadaci, ne da mi se ni pogledati! |
|
10% |
[ 1 ] |
|
| Ukupno glasova : 10 |
|
| Autor/ica |
Poruka |
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
 Postano: 0:09 pet, 20. 10. 2006 Naslov: Postano: 0:09 pet, 20. 10. 2006 Naslov: |
    |
|
|
OK, evo jedna zadacica za sljedece vjezbe.
Nije teska, ali ilustrira stvari kojih treba biti svjestan kad se barata s binarnom reprezentacijom objekata koji se razmjenjuju izmedju razlicitih sistema.
Definirajte funkciju
[code:1]bool isLittleEndian();[/code:1]
koja vraca true akko sistem na kojem se izvrsava koristi little endian poredak byte-ova, a false inace (big endian).
Definirajte potom funkcije
[code:1]T convertEndian(T);[/code:1]
za [b]prikladne[/b] primitivne tipove T, koje pretvaraju binarnu reprezentaciju iz sistemskog poretka byte-ova u "onaj drugi".
Naravno, implementacije ce biti skoro identicne, pa tu funkciju ima smisla uciniti predloskom, ali o tome kad iste naucimo...
Ako ne znate o cemu je tu rijec, pogledajte na Wikipediu.
Ako zelite i zanimljivu pripovijest u pozadini, posjetite predavanja prof. Ribarica iz Gradje racunala.
OK, evo jedna zadacica za sljedece vjezbe.
Nije teska, ali ilustrira stvari kojih treba biti svjestan kad se barata s binarnom reprezentacijom objekata koji se razmjenjuju izmedju razlicitih sistema.
Definirajte funkciju
| Kod: | | bool isLittleEndian(); |
koja vraca true akko sistem na kojem se izvrsava koristi little endian poredak byte-ova, a false inace (big endian).
Definirajte potom funkcije
za prikladne primitivne tipove T, koje pretvaraju binarnu reprezentaciju iz sistemskog poretka byte-ova u "onaj drugi".
Naravno, implementacije ce biti skoro identicne, pa tu funkciju ima smisla uciniti predloskom, ali o tome kad iste naucimo...
Ako ne znate o cemu je tu rijec, pogledajte na Wikipediu.
Ako zelite i zanimljivu pripovijest u pozadini, posjetite predavanja prof. Ribarica iz Gradje racunala.
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 9:38 pet, 20. 10. 2006 Naslov: Postano: 9:38 pet, 20. 10. 2006 Naslov: |
    |
|
|
@vsego: zaboravih reci da je <spoiler>[size=0]straight-forward u svim slucajevima[/size] </spoiler> moguc. Barem se i meni tako cini
@vsego: zaboravih reci da je <spoiler>straight-forward u svim slucajevima </spoiler> moguc. Barem se i meni tako cini
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 9:58 pet, 20. 10. 2006 Naslov: Postano: 9:58 pet, 20. 10. 2006 Naslov: |
    |
|
|
evo mali spoiler, kako rijesiti zadatak na trivijalan nacin za mxn matricu, m i n parni
<spoiler>[size=0]
krecemo iz [m-1][0]
-> [m-2][0]
-> [m-1][0]
-> [m-1][1] -> [m-2][1] -> [m-3][1]
-> [m-3][0]
i sada radimo zmiju do vrha po ta dva stupca
-> [m-4][0] -> [m-4][1] -> [m-5][1] -> [m-5][0] -> ...
dodjemo do [0][1], ako je bilo mx2 gotovo, inace
[0][1]->[0][2]
i sada opet radimo zmiju (po stupcima) do kraja
[0][2]->[1][2]->...->[m-1][2]
->[m-1][3]->[m-2][3]->...
i na kraju zavrsavamo u [0][n-1]
[/size]
</spoiler>
evo mali spoiler, kako rijesiti zadatak na trivijalan nacin za mxn matricu, m i n parni
<spoiler>
krecemo iz [m-1][0]
→ [m-2][0]
→ [m-1][0]
→ [m-1][1] → [m-2][1] → [m-3][1]
→ [m-3][0]
i sada radimo zmiju do vrha po ta dva stupca
→ [m-4][0] → [m-4][1] → [m-5][1] → [m-5][0] → ...
dodjemo do [0][1], ako je bilo mx2 gotovo, inace
[0][1]→[0][2]
i sada opet radimo zmiju (po stupcima) do kraja
[0][2]→[1][2]→...→[m-1][2]
→[m-1][3]→[m-2][3]→...
i na kraju zavrsavamo u [0][n-1]
</spoiler>
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
 Postano: 15:38 pon, 23. 10. 2006 Naslov: Postano: 15:38 pon, 23. 10. 2006 Naslov: |
    |
|
|
Zadatak 3:
(Bit ce obradjen na vjezbama 30. 10.)
Napisite [url=http://en.wikipedia.org/wiki/Reverse_Polish_notation]RPN[/url] kalkulator.
Kalkulator racuna s racionalnim brojevima i podrzava:
binarne operacije: + - * /
stog operacije: [u]dup[/u] (kodiran kao prazna linija unosa) i [u]pop[/u] (kodiran kao \)
Unos se obavlja liniju po liniju, svaka linija formatirana je kao:
[latex](\mathsf{broj}\mid\mathsf{operator})?((\mathsf{\llcorner\hskip-1bp\lrcorner broj})\mid(\mathsf{\llcorner\hskip-1bp\lrcorner operator}))^*[/latex]
Prazna linija (ne sadrzi nista osim eventualnih bjelina) predstavlja naredbu za dupliciranje broja na vrhu stoga ([u]dup[/u]).
Nakon ucitavanja i izvrsavanja jedne linije kalkulator ispisuje cjelokupan sadrzaj stoga i ceka na novu liniju (tzv. read-eval loop).
Recena petlja terminira se s EOF.
Dodatno, napisite program koji konvertira aritmeticke izraze iz infix u RPN (postfix) oblik.
Program prima 0, 1 ili 2 dodatna argumenta komandne linije.
Prvi opcionalni argument navodi ime datoteke koja sadrzi infiks izraze; ako nije naveden, podrazumijeva se stdin.
Drugi opcionalni argument navodi ime datoteke u koju treba spremiti dobivene RPN izraze; ako nije naveden, podrazumijeva se stdout.
Svaki redak unosa/izlaza predstavlja jedan izraz.
Detalji infix izraza prepusteni su na volju rjesavacu, ali moraju se podrzavati cijeli brojevi, cetiri osnovne binarne aritmeticke operacije i (okrugle) zagrade.
Postfix izraz mora biti kompatibilan s unosom RPN kalkulatora.
Zadatak 3:
(Bit ce obradjen na vjezbama 30. 10.)
Napisite RPN kalkulator.
Kalkulator racuna s racionalnim brojevima i podrzava:
binarne operacije: + - * /
stog operacije: dup (kodiran kao prazna linija unosa) i pop (kodiran kao \)
Unos se obavlja liniju po liniju, svaka linija formatirana je kao:
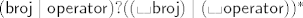
Prazna linija (ne sadrzi nista osim eventualnih bjelina) predstavlja naredbu za dupliciranje broja na vrhu stoga (dup).
Nakon ucitavanja i izvrsavanja jedne linije kalkulator ispisuje cjelokupan sadrzaj stoga i ceka na novu liniju (tzv. read-eval loop).
Recena petlja terminira se s EOF.
Dodatno, napisite program koji konvertira aritmeticke izraze iz infix u RPN (postfix) oblik.
Program prima 0, 1 ili 2 dodatna argumenta komandne linije.
Prvi opcionalni argument navodi ime datoteke koja sadrzi infiks izraze; ako nije naveden, podrazumijeva se stdin.
Drugi opcionalni argument navodi ime datoteke u koju treba spremiti dobivene RPN izraze; ako nije naveden, podrazumijeva se stdout.
Svaki redak unosa/izlaza predstavlja jedan izraz.
Detalji infix izraza prepusteni su na volju rjesavacu, ali moraju se podrzavati cijeli brojevi, cetiri osnovne binarne aritmeticke operacije i (okrugle) zagrade.
Postfix izraz mora biti kompatibilan s unosom RPN kalkulatora.
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
 Postano: 23:52 pon, 13. 11. 2006 Naslov: Postano: 23:52 pon, 13. 11. 2006 Naslov: |
    |
|
|
Zadatak 4:
Neka je [latex]\sigma\in S_n[/latex] proizvoljna permutacija.
Prikazite je kao produkt transpozicija.
Uputa:
Neka je [latex]\sigma(n)=k_n\ne n[/latex].
Nadalje, neka je [latex]\tau_n[/latex] transpozicija:
[latex]\tau_n(k_n)=n;\ \tau_n(n)=k_n;\ \tau_n(i)=i[/latex] za [latex]i\notin\left\lbrace k,n\right\rbrace[/latex].
Tada je [latex]\tau_n\sigma[/latex] permutacija t.d. [latex]\tau_n\sigma(n)=n[/latex].
Ako je [latex]\sigma(n)=n[/latex], stavimo [latex]\tau_n=\mathsf{id}[/latex].
Analogno, neka je [latex]\tau_n\sigma(n-1)=k_{n-1}\ne n-1[/latex].
Kao gore dobivamo transpoziciju [latex]\tau_{n-1}[/latex] t.d. vrijedi:
[latex]\tau_{n-1}\tau_n\sigma(i)=i[/latex] za [latex]i\in\left\lbrace n-1,n\right\rbrace[/latex].
Ako je [latex]\tau_n\sigma(n-1)=n-1[/latex], stavimo [latex]\tau_{n-1}=\mathsf{id}[/latex].
Ponavljanjem ovog postupka imamo:
[latex]\tau_2\cdots\tau_{n-1}\tau_n\sigma=\mathsf{id}[/latex]
odnosno, nakon pretumbavanja:
[latex]\tau_n^{-1}\tau_{n-1}^{-1}\cdots\tau_2^{-1}=\sigma[/latex]
gdje je, za neke [latex]i[/latex], moguce da je:
[latex]\tau_i=\mathsf{id}[/latex]
i takve [latex]\tau_i[/latex] ne ukljucujemo u trazeni produkt.
Zadatak 4:
Neka je 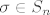 proizvoljna permutacija. proizvoljna permutacija.
Prikazite je kao produkt transpozicija.
Uputa:
Neka je 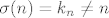 . .
Nadalje, neka je 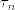 transpozicija: transpozicija:
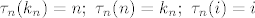 za za 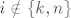 . .
Tada je 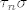 permutacija t.d. permutacija t.d. 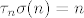 . .
Ako je 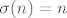 , stavimo , stavimo 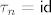 . .
Analogno, neka je 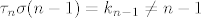 . .
Kao gore dobivamo transpoziciju 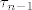 t.d. vrijedi: t.d. vrijedi:
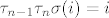 za za 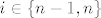 . .
Ako je 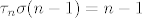 , stavimo , stavimo 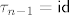 . .
Ponavljanjem ovog postupka imamo:
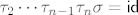
odnosno, nakon pretumbavanja:
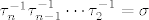
gdje je, za neke  , moguce da je: , moguce da je:
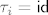
i takve 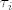 ne ukljucujemo u trazeni produkt. ne ukljucujemo u trazeni produkt.
|
|
| [Vrh] |
|
|







