| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 14:44 sub, 18. 11. 2006 Naslov: potprostori M+L i M presjek L Postano: 14:44 sub, 18. 11. 2006 Naslov: potprostori M+L i M presjek L |
    |
|
|
neka su M i L potprostori vektorskog prostora R^4 dani, redom svojim bazama
{(1,0,1,-2), (0,1,0,1)} i {(1,-1,-2,0), (0,2,3,-1)}
odredite po jednu bazu za M+L i M presjek L.
(LA1, 1. kolokvij, 30.11.2005.)
moze li mi netko objasniti kako se ovo rjesava jer smo do sada na vjezbama taman dosli do toga dijela, ali jos nismo poceli takve zadatke rjesavat.. :idea:
treba mi da bi provjezbao bolje stare kolokvije-da nemam stalno rupu od minimalno jednog zadatka..
helpic :oops:
p.s.thnx unaprijed :P
neka su M i L potprostori vektorskog prostora R^4 dani, redom svojim bazama
{(1,0,1,-2), (0,1,0,1)} i {(1,-1,-2,0), (0,2,3,-1)}
odredite po jednu bazu za M+L i M presjek L.
(LA1, 1. kolokvij, 30.11.2005.)
moze li mi netko objasniti kako se ovo rjesava jer smo do sada na vjezbama taman dosli do toga dijela, ali jos nismo poceli takve zadatke rjesavat.. 
treba mi da bi provjezbao bolje stare kolokvije-da nemam stalno rupu od minimalno jednog zadatka..
helpic 
p.s.thnx unaprijed 
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
 Postano: 18:24 sub, 18. 11. 2006 Naslov: Postano: 18:24 sub, 18. 11. 2006 Naslov: |
    |
|
|
Što se tiče baze za sumu, unija ovih dvaju skupova čini sistem izvodnica za M+L: {(1,0,1,-2), (0,1,0,1),(1,-1,-2,0), (0,2,3,-1)}, a s.i. se može reducirati do baze za M+L. I to je to. 8)
Za presjek nisam siguran, nek neka druga dobra duša ustupi. :wink:
Što se tiče baze za sumu, unija ovih dvaju skupova čini sistem izvodnica za M+L: {(1,0,1,-2), (0,1,0,1),(1,-1,-2,0), (0,2,3,-1)}, a s.i. se može reducirati do baze za M+L. I to je to. 
Za presjek nisam siguran, nek neka druga dobra duša ustupi. 
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 20:15 sub, 18. 11. 2006 Naslov: Postano: 20:15 sub, 18. 11. 2006 Naslov: |
    |
|
|
[quote="herman"]Što se tiče baze za sumu, unija ovih dvaju skupova čini sistem izvodnica za M+L: {(1,0,1,-2), (0,1,0,1),(1,-1,-2,0), (0,2,3,-1)}, a s.i. se može reducirati do baze za M+L. I to je to. 8) [/quote]
hmmm...dimenzija od M+L je 4. zasto bi se onda trebalo ista reducirati? u biti, ta 4 vektora bi onda po defaultu trebala biti linearno nezavisna, odnosno unija te dvije baze cini bazu za M+L odnosno R^4. ili je meni linearna totalno zahrdjala pa moram opet poceti citati citati knjigu prof. kurepe? :-)
| herman (napisa): | Što se tiče baze za sumu, unija ovih dvaju skupova čini sistem izvodnica za M+L: {(1,0,1,-2), (0,1,0,1),(1,-1,-2,0), (0,2,3,-1)}, a s.i. se može reducirati do baze za M+L. I to je to.  |
hmmm...dimenzija od M+L je 4. zasto bi se onda trebalo ista reducirati? u biti, ta 4 vektora bi onda po defaultu trebala biti linearno nezavisna, odnosno unija te dvije baze cini bazu za M+L odnosno R^4. ili je meni linearna totalno zahrdjala pa moram opet poceti citati citati knjigu prof. kurepe? 
|
|
| [Vrh] |
|
SickJedi
Moderator

Pridružen/a: 01. 10. 2004. (16:41:56)
Postovi: (3BC)16
Spol: 
Lokacija: Esperantija
|
 Postano: 20:27 sub, 18. 11. 2006 Naslov: Postano: 20:27 sub, 18. 11. 2006 Naslov: |
    |
|
|
[quote="HijenA"]hmmm...dimenzija od M+L je 4. zasto bi se onda trebalo ista reducirati? u biti, ta 4 vektora bi onda po defaultu trebala biti linearno nezavisna, odnosno unija te dvije baze cini bazu za M+L odnosno R^4.[/quote]
Nisam provjeravao za ovaj konkretni primjer, ali sma siguran da to opcenito ne vrijedi. Lako je naci kontraprimjer. Recimo baza za M je {(1,0,0,0), (0,1,0,0)}, a baza za L={(2,0,0,0),(0,0,1,0)}. Unijom dobijes skup od cetiri vektora koji ocito nisu baza za R^4.
| HijenA (napisa): | | hmmm...dimenzija od M+L je 4. zasto bi se onda trebalo ista reducirati? u biti, ta 4 vektora bi onda po defaultu trebala biti linearno nezavisna, odnosno unija te dvije baze cini bazu za M+L odnosno R^4. |
Nisam provjeravao za ovaj konkretni primjer, ali sma siguran da to opcenito ne vrijedi. Lako je naci kontraprimjer. Recimo baza za M je {(1,0,0,0), (0,1,0,0)}, a baza za L={(2,0,0,0),(0,0,1,0)}. Unijom dobijes skup od cetiri vektora koji ocito nisu baza za R^4.
|
|
| [Vrh] |
|
beba
Forumaš(ica)


Pridružen/a: 17. 08. 2006. (00:00:41)
Postovi: (41)16
Lokacija: st-ZG
|
 Postano: 21:30 sub, 18. 11. 2006 Naslov: Postano: 21:30 sub, 18. 11. 2006 Naslov: |
    |
|
|
evo jos jedan zadatak iz tog kolokvija.5 zadatak.neka je s skup=(x,y,z,w)R˘4:(2z-3x+6y=0,x-2y=-2w,z-x+2y+w=0).provjeri da je s vektorski prostor te mu nadi bazu i nadopuni je do baze za R^4.kako se provjerava da j eto vektorski prostor?mi na vjezbama samo provjeravali samo da je nesto vek. potprostor.
evo jos jedan zadatak iz tog kolokvija.5 zadatak.neka je s skup=(x,y,z,w)R˘4:(2z-3x+6y=0,x-2y=-2w,z-x+2y+w=0).provjeri da je s vektorski prostor te mu nadi bazu i nadopuni je do baze za R^4.kako se provjerava da j eto vektorski prostor?mi na vjezbama samo provjeravali samo da je nesto vek. potprostor.
|
|
| [Vrh] |
|
SickJedi
Moderator

Pridružen/a: 01. 10. 2004. (16:41:56)
Postovi: (3BC)16
Spol: 
Lokacija: Esperantija
|
|
| [Vrh] |
|
Gost
|
 Postano: 0:01 ned, 19. 11. 2006 Naslov: Postano: 0:01 ned, 19. 11. 2006 Naslov: |
    |
|
|
[quote:evo jos jedan zadatak iz tog kolokvija.5 zadatak.neka je s skup=(x,y,z,w)R˘4:(2z-3x+6y=0,x-2y=-2w,z-x+2y+w=0).provjeri da je s vektorski prostor te mu nadi bazu i nadopuni je do baze za R^4.kako se provjerava da j eto vektorski prostor?mi na vjezbama samo provjeravali samo da je nesto vek. potprostor.
Ja mislim da bi se to trebalo provjeravati na sljedeći način:
Uzmemo dva vektora (x,y,z,w) i (x1,y1,z1,w1) iz S.
A(x,y,z,w)+B(x1,y1,z1,w1) je onda također iz S.
Sada treba provjeriti gornje uvjete, tj.
2(Az+Bz1)-3(Ax+Bx1)+6(Ay+By)=0
A(2z-3x+6y)+B(2z1-3x1+6y1)=0
A*0 + B*0=0 što je zadovoljeno za svaki A i B.
Analogno treba provjeriti i ostale uvjete.
Ps. Ako netko sa više znanja nađe nekakvu grešku, molio bih ga da me ispravi. Unaprijed hvala! :)
[/quote]
[quote:evo jos jedan zadatak iz tog kolokvija.5 zadatak.neka je s skup=(x,y,z,w)R˘4:(2z-3x+6y=0,x-2y=-2w,z-x+2y+w=0).provjeri da je s vektorski prostor te mu nadi bazu i nadopuni je do baze za R^4.kako se provjerava da j eto vektorski prostor?mi na vjezbama samo provjeravali samo da je nesto vek. potprostor.
Ja mislim da bi se to trebalo provjeravati na sljedeći način:
Uzmemo dva vektora (x,y,z,w) i (x1,y1,z1,w1) iz S.
A(x,y,z,w)+B(x1,y1,z1,w1) je onda također iz S.
Sada treba provjeriti gornje uvjete, tj.
2(Az+Bz1)-3(Ax+Bx1)+6(Ay+By)=0
A(2z-3x+6y)+B(2z1-3x1+6y1)=0
A*0 + B*0=0 što je zadovoljeno za svaki A i B.
Analogno treba provjeriti i ostale uvjete.
Ps. Ako netko sa više znanja nađe nekakvu grešku, molio bih ga da me ispravi. Unaprijed hvala! 
[/quote]
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 0:34 ned, 19. 11. 2006 Naslov: Postano: 0:34 ned, 19. 11. 2006 Naslov: |
    |
|
|
[quote="HijenA"]
...dimenzija od M+L je 4. zasto bi se onda trebalo ista reducirati? u biti, ta 4 vektora bi onda po defaultu trebala biti linearno nezavisna, odnosno unija te dvije baze cini bazu za M+L [b]odnosno R^4[/b]. ili je meni [i]linearna totalno zahrdjala[/i]...[/quote]
[b]boldano[/b]= baza za uniju ne treba biti iste dimenzije kao i vp R^4, tj ako je unija vekt potprostor od R^4 onda ta ista unija moze imati dim=0,1,2,3,4
[i]koso[/i]= malo jest zahrdjala :twisted:
p.s. zad se bez problema rijesi s onim 1. objasnjenjem( i mislim da je dim(M+L) ispala bas u zad <4) :)
samo me jos muci M presjek L!!!!!! :?
| HijenA (napisa): |
...dimenzija od M+L je 4. zasto bi se onda trebalo ista reducirati? u biti, ta 4 vektora bi onda po defaultu trebala biti linearno nezavisna, odnosno unija te dvije baze cini bazu za M+L odnosno R^4. ili je meni linearna totalno zahrdjala... |
boldano= baza za uniju ne treba biti iste dimenzije kao i vp R^4, tj ako je unija vekt potprostor od R^4 onda ta ista unija moze imati dim=0,1,2,3,4
koso= malo jest zahrdjala 
p.s. zad se bez problema rijesi s onim 1. objasnjenjem( i mislim da je dim(M+L) ispala bas u zad <4) 
samo me jos muci M presjek L!!!!!! 
Zadnja promjena: 13_mac; 0:40 ned, 19. 11. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 0:35 ned, 19. 11. 2006 Naslov: Postano: 0:35 ned, 19. 11. 2006 Naslov: |
    |
|
|
[quote="Anonymous"][quote:evo jos jedan zadatak iz tog kolokvija.5 zadatak.neka je s skup=(x,y,z,w)R˘4:(2z-3x+6y=0,x-2y=-2w,z-x+2y+w=0).provjeri da je s vektorski prostor te mu nadi bazu i nadopuni je do baze za R^4.kako se provjerava da j eto vektorski prostor?mi na vjezbama samo provjeravali samo da je nesto vek. potprostor.
Ja mislim da bi se to trebalo provjeravati na sljedeći način:
Uzmemo dva vektora (x,y,z,w) i (x1,y1,z1,w1) iz S.
A(x,y,z,w)+B(x1,y1,z1,w1) je onda također iz S.
Sada treba provjeriti gornje uvjete, tj.
2(Az+Bz1)-3(Ax+Bx1)+6(Ay+By)=0
A(2z-3x+6y)+B(2z1-3x1+6y1)=0
A*0 + B*0=0 što je zadovoljeno za svaki A i B.
Analogno treba provjeriti i ostale uvjete.
Ps. Ako netko sa više znanja nađe nekakvu grešku, molio bih ga da me ispravi. Unaprijed hvala! :)
[/quote]
tocno tako
| Anonymous (napisa): | [quote:evo jos jedan zadatak iz tog kolokvija.5 zadatak.neka je s skup=(x,y,z,w)R˘4:(2z-3x+6y=0,x-2y=-2w,z-x+2y+w=0).provjeri da je s vektorski prostor te mu nadi bazu i nadopuni je do baze za R^4.kako se provjerava da j eto vektorski prostor?mi na vjezbama samo provjeravali samo da je nesto vek. potprostor.
Ja mislim da bi se to trebalo provjeravati na sljedeći način:
Uzmemo dva vektora (x,y,z,w) i (x1,y1,z1,w1) iz S.
A(x,y,z,w)+B(x1,y1,z1,w1) je onda također iz S.
Sada treba provjeriti gornje uvjete, tj.
2(Az+Bz1)-3(Ax+Bx1)+6(Ay+By)=0
A(2z-3x+6y)+B(2z1-3x1+6y1)=0
A*0 + B*0=0 što je zadovoljeno za svaki A i B.
Analogno treba provjeriti i ostale uvjete.
Ps. Ako netko sa više znanja nađe nekakvu grešku, molio bih ga da me ispravi. Unaprijed hvala! 
|
tocno tako
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 11:54 ned, 19. 11. 2006 Naslov: Re: potprostori M+L i M presjek L Postano: 11:54 ned, 19. 11. 2006 Naslov: Re: potprostori M+L i M presjek L |
    |
|
|
[quote="13_mac"]neka su M i L potprostori vektorskog prostora R^4 dani, redom svojim bazama
{(1,0,1,-2), (0,1,0,1)} i {(1,-1,-2,0), (0,2,3,-1)}
odredite po jednu bazu za M+L i M presjek L.
(LA1, 1. kolokvij, 30.11.2005.)
moze li mi netko objasniti kako se ovo rjesava jer smo do sada na vjezbama taman dosli do toga dijela, ali jos nismo poceli takve zadatke rjesavat.. :idea:
treba mi da bi provjezbao bolje stare kolokvije-da nemam stalno rupu od minimalno jednog zadatka..
helpic :oops:
p.s.thnx unaprijed :P[/quote]
Prvo odrediš bazu za uniju, dobiješ da je to skup [latex]\left\{ {\left( {{\rm 1}{\rm ,0}{\rm ,1}{\rm , - 2}} \right),\left( {0,1,0,1} \right),\left( {1, - 1, - 2,0} \right)} \right\}[/latex].
Neka je [latex]a_1 = \left( {{\rm 1}{\rm ,0}{\rm ,1}{\rm , - 2}} \right),a_2 = \left( {0,1,0,1} \right),b_1 = \left( {1, - 1, - 2,0} \right),b_2 = \left( {0,2,3, - 1} \right)[/latex].
Kako mi je [latex]\left\{ {a_1 ,a_2 ,b_1 } \right\}[/latex] baza za [latex]M \cup L[/latex], posebno i vektor [latex]b_2 \in L \subseteq M \cup L[/latex] mogu prikazati pomoću te baze, pa imam [latex]b_2 = \alpha _1 a_1 + \alpha _2 a_2 + \beta _1 b_1[/latex] [latex]\Leftrightarrow b_2 - \beta _1 b_1 [/latex][latex] = \alpha _1 a_1 + \alpha _2 a_2[/latex], a vektor s lijeve strane je iz L, a s desne iz M, ali kako vrijedi jednakost, očito je i vektor s desne strane i iz L, što zapravo znači da je iz [latex]M \cap L[/latex].
Sad odredimo taj vektor, dobijemo da je [latex]\alpha _1 = \alpha _2 = 1,\beta _1 = - 1 \Rightarrow \alpha _1 a_1 + \alpha _2 a_2 = \left( {{\rm 1}{\rm ,0}{\rm ,1}{\rm , - 2}} \right) + \left( {0,1,0,1} \right) = \left( {1,1,1, - 1} \right)[/latex]. Kako je [latex]\dim M \cap L = \dim M + \dim L - \dim M \cup L = 2 + 2 - 3 = 1[/latex], dobivamo da je [latex]\left\{ {\left( {1,1,1, - 1} \right)} \right\}[/latex] baza za [latex]M \cap L[/latex].
Dođite na demonstrature, srijedom u 16:00 u 004.
| 13_mac (napisa): | neka su M i L potprostori vektorskog prostora R^4 dani, redom svojim bazama
{(1,0,1,-2), (0,1,0,1)} i {(1,-1,-2,0), (0,2,3,-1)}
odredite po jednu bazu za M+L i M presjek L.
(LA1, 1. kolokvij, 30.11.2005.)
moze li mi netko objasniti kako se ovo rjesava jer smo do sada na vjezbama taman dosli do toga dijela, ali jos nismo poceli takve zadatke rjesavat.. 
treba mi da bi provjezbao bolje stare kolokvije-da nemam stalno rupu od minimalno jednog zadatka..
helpic 
p.s.thnx unaprijed  |
Prvo odrediš bazu za uniju, dobiješ da je to skup 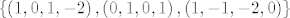 . .
Neka je 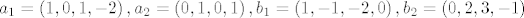 . .
Kako mi je 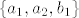 baza za baza za 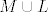 , posebno i vektor , posebno i vektor 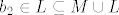 mogu prikazati pomoću te baze, pa imam mogu prikazati pomoću te baze, pa imam 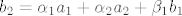  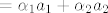 , a vektor s lijeve strane je iz L, a s desne iz M, ali kako vrijedi jednakost, očito je i vektor s desne strane i iz L, što zapravo znači da je iz , a vektor s lijeve strane je iz L, a s desne iz M, ali kako vrijedi jednakost, očito je i vektor s desne strane i iz L, što zapravo znači da je iz 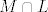 . .
Sad odredimo taj vektor, dobijemo da je 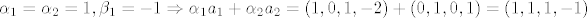 . Kako je . Kako je 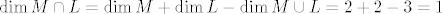 , dobivamo da je , dobivamo da je 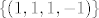 baza za baza za 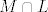 . .
Dođite na demonstrature, srijedom u 16:00 u 004.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Gost
|
 Postano: 14:41 ned, 19. 11. 2006 Naslov: Postano: 14:41 ned, 19. 11. 2006 Naslov: |
    |
|
|
Nije mi jasno, zašto kod onog prebacivanja vektora b1 i zaključivanja, ''jednakost vrijedi, pa je on i u L'' nisam isto tako mogao prebaciti a1 i doći do sličnog zaključka, pa zadatak riješiti preko a1?
U zadnjem dijelu zadatka, si išao od one činjenice da su u n dimenzionalnom prostoru n+1 vektora linerarno ovisni. Znao si da je ptprostor manje dimenzije? I ono o prikazu n-tog bektora kao lin. kombinacije prethodnika?
Nije mi jasno, zašto kod onog prebacivanja vektora b1 i zaključivanja, ''jednakost vrijedi, pa je on i u L'' nisam isto tako mogao prebaciti a1 i doći do sličnog zaključka, pa zadatak riješiti preko a1?
U zadnjem dijelu zadatka, si išao od one činjenice da su u n dimenzionalnom prostoru n+1 vektora linerarno ovisni. Znao si da je ptprostor manje dimenzije? I ono o prikazu n-tog bektora kao lin. kombinacije prethodnika?
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 15:14 ned, 19. 11. 2006 Naslov: Postano: 15:14 ned, 19. 11. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]Nije mi jasno, zašto kod onog prebacivanja vektora b1 i zaključivanja, ''jednakost vrijedi, pa je on i u L'' nisam isto tako mogao prebaciti a1 i doći do sličnog zaključka, pa zadatak riješiti preko a1?
U zadnjem dijelu zadatka, si išao od one činjenice da su u n dimenzionalnom prostoru n+1 vektora linerarno ovisni. Znao si da je ptprostor manje dimenzije? I ono o prikazu n-tog bektora kao lin. kombinacije prethodnika?[/quote]
Sry, nemam vremena odgovarat, dođite na demonstrature pa ću vam objasnit. Ako nije hitno, mogu odgovorit nakon 6.12. ili se nađe neka dobra duša koja će napisat odgovor. Hvala na razumjevanju
| Anonymous (napisa): | Nije mi jasno, zašto kod onog prebacivanja vektora b1 i zaključivanja, ''jednakost vrijedi, pa je on i u L'' nisam isto tako mogao prebaciti a1 i doći do sličnog zaključka, pa zadatak riješiti preko a1?
U zadnjem dijelu zadatka, si išao od one činjenice da su u n dimenzionalnom prostoru n+1 vektora linerarno ovisni. Znao si da je ptprostor manje dimenzije? I ono o prikazu n-tog bektora kao lin. kombinacije prethodnika? |
Sry, nemam vremena odgovarat, dođite na demonstrature pa ću vam objasnit. Ako nije hitno, mogu odgovorit nakon 6.12. ili se nađe neka dobra duša koja će napisat odgovor. Hvala na razumjevanju
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 17:53 ned, 19. 11. 2006 Naslov: Postano: 17:53 ned, 19. 11. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]Nije mi jasno, zašto kod onog prebacivanja vektora b1 i zaključivanja, ''jednakost vrijedi, pa je on i u L'' nisam isto tako mogao prebaciti a1 i doći do sličnog zaključka, pa zadatak riješiti preko a1?[/quote]
mogao si doci i preko a1(vjerovatno si krivo nesto pomnozio, zbrojio :roll: ), u slucaju da si kod trazenja baze koristio a1 kao zadnji, tj,:
1° a2=x*b1 -->nema rj
2° a2=x*b1 + y*b2 -->nema rj.
3° a2=x*b1 + y*b2 + [b]z*a1[/b] -->[b]ima rj.[/b] (uoci boldano :wink: )
=> {a2, b1, b2} baza za M+L, itd....
tako da se nadalje rjesavanje svodi na isti nacin kao da si uzeo b2.. 8)
p.s. na kraju dobijes za M presjek L isto rj bez obzira da li si rjesavao preko a1 ili b2!
[quote="Anonymous"]U zadnjem dijelu zadatka, si išao od one činjenice da su u n dimenzionalnom prostoru n+1 vektora linerarno ovisni.[/quote]
ispravak: u n-dim prostoru [b]skup vektora broja n+1[/b] je uvijek lin zav
-->nepotrebno za ovaj zad, ali ti to mora biti negdje u podsvijesti 8)
[quote="Anonymous"] Znao si da je ptprostor manje dimenzije?[/quote]
ne znam je li to kolega znao, ali ponavljam, nije uopce bitno da li je znao ili nije jer [b]racunom dodjes do svega potrebnog[/b]!
(mala napomena: mislim, nisam siguran, da je neki logicki zakljucak da je M presjek L manje dimenzije od M+L, nacrtaj za provjeru!)
p.s. potprostor uopce ne mora biti manje dimenzije, moze biti [b]jednake ili manje[/b] od tog nekog prostora
[quote="Anonymous"]I ono o prikazu n-tog bektora kao lin. kombinacije prethodnika?[/quote]
kolega, meni malo steka LA1, ali s ovom izjavom vidim da ima netko tko je u goroj poziciji od mene :twisted: no offence, ali prouci PUNO bolje predavanja i idi sad ovaj zadnji tjedan na sve zive i nezive konzultacije i demonstrature (kao sto cu i ja vjerovatno) :wink: -->krajnje je vrijeme 8)
moje isprike ako sam nesto falšao(slobodno me ispravite, pokudite
:P )
| Anonymous (napisa): | | Nije mi jasno, zašto kod onog prebacivanja vektora b1 i zaključivanja, ''jednakost vrijedi, pa je on i u L'' nisam isto tako mogao prebaciti a1 i doći do sličnog zaključka, pa zadatak riješiti preko a1? |
mogao si doci i preko a1(vjerovatno si krivo nesto pomnozio, zbrojio  ), u slucaju da si kod trazenja baze koristio a1 kao zadnji, tj,: ), u slucaju da si kod trazenja baze koristio a1 kao zadnji, tj,:
1° a2=x*b1 →nema rj
2° a2=x*b1 + y*b2 →nema rj.
3° a2=x*b1 + y*b2 + z*a1 →ima rj. (uoci boldano  ) )
⇒ {a2, b1, b2} baza za M+L, itd....
tako da se nadalje rjesavanje svodi na isti nacin kao da si uzeo b2.. 
p.s. na kraju dobijes za M presjek L isto rj bez obzira da li si rjesavao preko a1 ili b2!
| Anonymous (napisa): | | U zadnjem dijelu zadatka, si išao od one činjenice da su u n dimenzionalnom prostoru n+1 vektora linerarno ovisni. |
ispravak: u n-dim prostoru skup vektora broja n+1 je uvijek lin zav
→nepotrebno za ovaj zad, ali ti to mora biti negdje u podsvijesti 
| Anonymous (napisa): | | Znao si da je ptprostor manje dimenzije? |
ne znam je li to kolega znao, ali ponavljam, nije uopce bitno da li je znao ili nije jer racunom dodjes do svega potrebnog!
(mala napomena: mislim, nisam siguran, da je neki logicki zakljucak da je M presjek L manje dimenzije od M+L, nacrtaj za provjeru!)
p.s. potprostor uopce ne mora biti manje dimenzije, moze biti jednake ili manje od tog nekog prostora
| Anonymous (napisa): | | I ono o prikazu n-tog bektora kao lin. kombinacije prethodnika? |
kolega, meni malo steka LA1, ali s ovom izjavom vidim da ima netko tko je u goroj poziciji od mene  no offence, ali prouci PUNO bolje predavanja i idi sad ovaj zadnji tjedan na sve zive i nezive konzultacije i demonstrature (kao sto cu i ja vjerovatno) no offence, ali prouci PUNO bolje predavanja i idi sad ovaj zadnji tjedan na sve zive i nezive konzultacije i demonstrature (kao sto cu i ja vjerovatno)  →krajnje je vrijeme →krajnje je vrijeme 
moje isprike ako sam nesto falšao(slobodno me ispravite, pokudite
 ) )
|
|
| [Vrh] |
|
vanish
Forumaš(ica)


Pridružen/a: 02. 10. 2005. (22:45:35)
Postovi: (6D)16
Spol: 
Lokacija: stambena zgrada
|
 Postano: 19:11 ned, 19. 11. 2006 Naslov: Re: potprostori M+L i M presjek L Postano: 19:11 ned, 19. 11. 2006 Naslov: Re: potprostori M+L i M presjek L |
    |
|
|
[quote="alen"]
Prvo odrediš bazu za uniju....[/quote]
Dobro, ja nisam demos iz LA, ali čini mi se da unija potprostora općenito nije potprostor. Odrediš bazu za M+L, najmanji potprostor koji sadrži uniju.
[quote="alen"]
Kako je [latex]\dim M \cap L = \dim M + \dim L - \dim M \cup L = 2 + 2 - 3 = 1[/latex], dobivamo da je [latex]\left\{ {\left( {1,1,1, - 1} \right)} \right\}[/latex] baza za [latex]M \cap L[/latex].
[/quote]
U formuli se treba isto zamijenit unija sa sumom.
| alen (napisa): |
Prvo odrediš bazu za uniju.... |
Dobro, ja nisam demos iz LA, ali čini mi se da unija potprostora općenito nije potprostor. Odrediš bazu za M+L, najmanji potprostor koji sadrži uniju.
| alen (napisa): |
Kako je 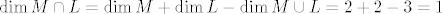 , dobivamo da je , dobivamo da je 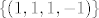 baza za baza za 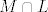 . .
|
U formuli se treba isto zamijenit unija sa sumom.
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
 Postano: 19:13 ned, 19. 11. 2006 Naslov: Postano: 19:13 ned, 19. 11. 2006 Naslov: |
    |
|
|
[quote="alen"]Sry, nemam vremena odgovarat, dođite na demonstrature pa ću vam objasnit. Ako nije hitno, mogu odgovorit nakon 6.12. ili se nađe neka dobra duša koja će napisat odgovor. Hvala na razumjevanju[/quote]
Malo lakse s tim SPA, vidis kako ti se sve zamutilo, odjednom + postaje U, ako ovako nastavis vise neces znat ni definiciju limesa :twisted: .
Sva sreca da imamo super_vanish :dance3:
| alen (napisa): | | Sry, nemam vremena odgovarat, dođite na demonstrature pa ću vam objasnit. Ako nije hitno, mogu odgovorit nakon 6.12. ili se nađe neka dobra duša koja će napisat odgovor. Hvala na razumjevanju |
Malo lakse s tim SPA, vidis kako ti se sve zamutilo, odjednom + postaje U, ako ovako nastavis vise neces znat ni definiciju limesa  . .
Sva sreca da imamo super_vanish 
_________________ Kad sam bila mala htjela sam biti statističarka 
[tex]\omega \in \Omega[/tex] 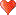 |
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
|













