| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
 Postano: 14:03 sri, 29. 11. 2006 Naslov: Postano: 14:03 sri, 29. 11. 2006 Naslov: |
    |
|
|
Dok smišljate i trežite greške u prethodnom zadatku evo još jednog (trivijalnog) iz prošlogodišnjih kolokvija...
Treba ispitati jesu li sljedeći vektori lin. zav ili nezav. u [latex]V^3(O)[/latex]
A = (-3, 1, 1),
B = (2, 3, 4),
C = (8, 1, 2)
Ubacimo u algebarski kriterij...
[latex]\alpha (-3, 1, 1) + \beta (2,3,4) + \gamma (8, 1, 2) = (0, 0, 0)\\
\\
-3\alpha + 2\beta + 8\gamma = 0\\
\alpha + 3\beta + \gamma = 0\\
\alpha + 4\beta + 2\gamma = 0[/latex]
oduzmem drugu jednadžbu od prve, pa imam:
[latex]\beta + \gamma = 0\\
\beta = -\gamma[/latex]
Upadnem u neku drugu jednadžb i dobijem da je:
[latex]\alpha = -2\beta[/latex]
Rješenje mogu zapisati kao [latex]\{-2\beta, \beta, -\beta\}[/latex]
Zaključak: vektori su linearno ovisni, dakle komplanarni.
Dok smišljate i trežite greške u prethodnom zadatku evo još jednog (trivijalnog) iz prošlogodišnjih kolokvija...
Treba ispitati jesu li sljedeći vektori lin. zav ili nezav. u 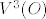
A = (-3, 1, 1),
B = (2, 3, 4),
C = (8, 1, 2)
Ubacimo u algebarski kriterij...
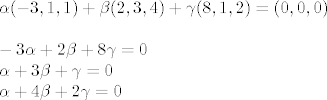
oduzmem drugu jednadžbu od prve, pa imam:
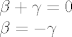
Upadnem u neku drugu jednadžb i dobijem da je:

Rješenje mogu zapisati kao 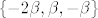
Zaključak: vektori su linearno ovisni, dakle komplanarni.
_________________
"Žalim prošlost, nadam se budućnosti, nezadovoljan sa sadošnošću - to je moj život."
-Pjotr Iljič Čajkovski
|
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
 Postano: 15:14 sri, 29. 11. 2006 Naslov: Postano: 15:14 sri, 29. 11. 2006 Naslov: |
    |
|
|
Evo još jedan iz kolokvija, malo je pipkav zato što ima zaključivanja (a to nije dobro :P )
Neka je [latex]\mathcal{P}_3[/latex] vektorski prostor polinoma stupnja [latex]\ge 3[/latex]. (Dimenzija tog prostora je 4.)
b) Je li skup [latex]\{1, 2t + 1, t^3, t^3 - t^2\}[/latex] sustav izvodnica za [latex]\mathcal{P}_3[/latex]?
Razmišljam se ovako... dani skup mi ima 4 elementa, hm, vidim da se radi o 4. dimenzionalnom prostoru, pa ako je taj skup linearno neovisan, nužno je baza, dakle i skup izvodnica, zato što znamo da se svaki skup izvodnica dâ reducirati do baze.
Idem probati:
[latex]\alpha + \beta (2t + 1) + \gamma t^3 + \delta (t^3 - t^2) = (0, 0, 0, 0)\\[/latex]
Zapišem to ovako:
[latex]\alpha + \beta = 0\\
2\beta = 0\\
-\gamma = 0\\
\delta + \gamma = 0[/latex]
odnosno:
[latex]\alpha = - \beta\\
\beta = 0 \Rightarrow \alpha = 0\\
\gamma = 0\\
\delta = 0[/latex]
I eto ga... naravno, ako nisam negdje u početku fulao kada sam pretpostavljao sve i svašta i kada sam to ovdje rješavao, bez da sam prethodno riješio na papiru :).
Evo još jedan iz kolokvija, malo je pipkav zato što ima zaključivanja (a to nije dobro  ) )
Neka je 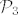 vektorski prostor polinoma stupnja vektorski prostor polinoma stupnja 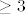 . (Dimenzija tog prostora je 4.) . (Dimenzija tog prostora je 4.)
b) Je li skup 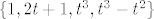 sustav izvodnica za sustav izvodnica za 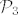 ? ?
Razmišljam se ovako... dani skup mi ima 4 elementa, hm, vidim da se radi o 4. dimenzionalnom prostoru, pa ako je taj skup linearno neovisan, nužno je baza, dakle i skup izvodnica, zato što znamo da se svaki skup izvodnica dâ reducirati do baze.
Idem probati:
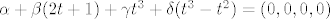
Zapišem to ovako:
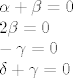
odnosno:
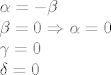
I eto ga... naravno, ako nisam negdje u početku fulao kada sam pretpostavljao sve i svašta i kada sam to ovdje rješavao, bez da sam prethodno riješio na papiru  . .
_________________
"Žalim prošlost, nadam se budućnosti, nezadovoljan sa sadošnošću - to je moj život."
-Pjotr Iljič Čajkovski
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 17:21 sri, 29. 11. 2006 Naslov: Postano: 17:21 sri, 29. 11. 2006 Naslov: |
    |
|
|
ovaj zadatak sa a*x + y = b....
ima 2 slucaja:
1)det A != 0, a != -2, 2 => [b]x = (a*b - 2) / (a^2 - 4), y = (2*a - 4*b) / (a^2 - 4)[/b]
2)det A = 0 => a = -2, 2 :
2.1) [i][b]a = -2[/b][/i] (...rjesavas sustav...)=> b = 2, b != 2
2.1.1)[b]b != 2, => nema rjesenja[/b]
2.1.2)[b]b = 2 => y = 2*x - 2, x e R, tj. beskonacno 1-param rjesenja[/b]
2.2)[i][b]a = 2[/b][/i] (...rjesavas sustav...)=> b = 1, b != 1
2.2.1) [b]b != 1 => nema rjesenja[/b]
2.2.2) [b]b = 1 => y = 1 - 2x, x e R, tj. beskonacno 1-param rjesenja[/b]
uoci => != znaci razlicito, x e R (x element iz R), podebljano su ti rjesenja, tako da je [u][b]konacno rjesenje[/b][/u]:
[color=darkred]za a != -2, 2 imamo jedinstveno rjesenje koje iznosi x = ..., y = ...(ono gore pod 1))[/color], [color=orange]za a = -2 i b != 2 nema rjesenja[/color], [color=green]za a = -2 i b = 2 rjesenje je y = 2*x - 2, x e R(besk 1 - param rjesenja)[/color],[color=blue] za a = 2 i b != 1 nema rjesenja[/color], [color=violet]za a = 2 i b = 1 rjesenje je y = 1 - 2*x, x e R(besk 1 - param rjesenja)[/color]
ovaj zadatak sa a*x + y = b....
ima 2 slucaja:
1)det A != 0, a != -2, 2 ⇒ x = (a*b - 2) / (a^2 - 4), y = (2*a - 4*b) / (a^2 - 4)
2)det A = 0 ⇒ a = -2, 2 :
2.1) a = -2 (...rjesavas sustav...)⇒ b = 2, b != 2
2.1.1)b != 2, ⇒ nema rjesenja
2.1.2)b = 2 ⇒ y = 2*x - 2, x e R, tj. beskonacno 1-param rjesenja
2.2)a = 2 (...rjesavas sustav...)⇒ b = 1, b != 1
2.2.1) b != 1 ⇒ nema rjesenja
2.2.2) b = 1 ⇒ y = 1 - 2x, x e R, tj. beskonacno 1-param rjesenja
uoci ⇒ != znaci razlicito, x e R (x element iz R), podebljano su ti rjesenja, tako da je konacno rjesenje:
za a != -2, 2 imamo jedinstveno rjesenje koje iznosi x = ..., y = ...(ono gore pod 1)), za a = -2 i b != 2 nema rjesenja, za a = -2 i b = 2 rjesenje je y = 2*x - 2, x e R(besk 1 - param rjesenja), za a = 2 i b != 1 nema rjesenja, za a = 2 i b = 1 rjesenje je y = 1 - 2*x, x e R(besk 1 - param rjesenja)
|
|
| [Vrh] |
|
Gost
|
 Postano: 17:37 sri, 29. 11. 2006 Naslov: Postano: 17:37 sri, 29. 11. 2006 Naslov: |
    |
|
|
nesto mi nije jasno... imali smo na vjezbama dva zadatka. u oba treba reci da li su lin nez, baza i s.i.
1. { 1-t+t^2, 1-t-t^2, 1-t+2t^2, 1-t } u P2
2. { (1,0,1) (2,1,1) (2,-2,3) (4,1,3) (1,1,0) } u [b]R[/b]^3
i sad...
za prvi zadatak smo odmah rekli da nije baza jer ima 4 elementa, da nije lin nez zbog istog razloga, te provjeravamo da li je s.i. . nakon provjere za s.i. dobijemo da nije s.i. jer u skupu imamo 2 lin nezavisna polinoma ( a zadnja 2 smo izbacili). a sto bi bilo da smo izbacili samo 1 polinom i da su nam ostala tri, onda bi trebalo biti baza a mi smo odmah na pocetku rekli da nije...
u drugom zadatku smo prvo izbacili zavisne vektore (zadnja dva) i onda rekli da je baza jer je nezavisan ,a da je skup od kojeg smo krenuli s.i.
zasto smo u prvom zadatku odmah rekli da je lin nezavisan pocetni skup, dok smo u drugom o nezavisnosti razmisljali tek kad smo izbacili one zavisne i dobili novi skup bez zadnja 2? isto tako smo za drugi zadatak moglu odmah kao za prvi reci da nije baza jer ima 5 elemenata a dim=3.
dakle, pitanje bi bilo, da li ja nezavisnost, bazu i s.i. odredjujem tek nakon sto sredim skup (izbacim nezavisne) ili odmah na pocetku (kako je rekao prvi primjer).
nadam se da ce netko skuziti sto pitam...
:cry:
nesto mi nije jasno... imali smo na vjezbama dva zadatka. u oba treba reci da li su lin nez, baza i s.i.
1. { 1-t+t^2, 1-t-t^2, 1-t+2t^2, 1-t } u P2
2. { (1,0,1) (2,1,1) (2,-2,3) (4,1,3) (1,1,0) } u R^3
i sad...
za prvi zadatak smo odmah rekli da nije baza jer ima 4 elementa, da nije lin nez zbog istog razloga, te provjeravamo da li je s.i. . nakon provjere za s.i. dobijemo da nije s.i. jer u skupu imamo 2 lin nezavisna polinoma ( a zadnja 2 smo izbacili). a sto bi bilo da smo izbacili samo 1 polinom i da su nam ostala tri, onda bi trebalo biti baza a mi smo odmah na pocetku rekli da nije...
u drugom zadatku smo prvo izbacili zavisne vektore (zadnja dva) i onda rekli da je baza jer je nezavisan ,a da je skup od kojeg smo krenuli s.i.
zasto smo u prvom zadatku odmah rekli da je lin nezavisan pocetni skup, dok smo u drugom o nezavisnosti razmisljali tek kad smo izbacili one zavisne i dobili novi skup bez zadnja 2? isto tako smo za drugi zadatak moglu odmah kao za prvi reci da nije baza jer ima 5 elemenata a dim=3.
dakle, pitanje bi bilo, da li ja nezavisnost, bazu i s.i. odredjujem tek nakon sto sredim skup (izbacim nezavisne) ili odmah na pocetku (kako je rekao prvi primjer).
nadam se da ce netko skuziti sto pitam...

|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 18:50 sri, 29. 11. 2006 Naslov: Postano: 18:50 sri, 29. 11. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]...a sto bi bilo da smo izbacili samo 1 polinom i da su nam ostala tri, onda bi trebalo biti baza a mi smo odmah na pocetku rekli da nije...
[/quote]
ako bi ta tri koja su ostala bili linearno nezavisni onda bi to znacilo da 3 elementa, [b]linearno nezavisna u prostoru P2 cine BAZU[/b] =>odmah kad je baza onda je sigurno i [b]sistem izvodnica ZA vekt prostor P2[/b]
2. ako se trazi baza/ sist. izv./ lin. nez. [b]u P2[/b] onda ovo gore sta sam rekao stoji!
(uoci boldano :wink: )
[quote="Anonymous"]u drugom zadatku smo prvo izbacili zavisne vektore (zadnja dva) i onda rekli da je baza jer je nezavisan ,a da je skup od kojeg smo krenuli s.i.
[b]zasto smo u prvom zadatku odmah rekli da je lin nezavisan pocetni skup, dok smo u drugom o nezavisnosti razmisljali tek kad smo izbacili one zavisne i dobili novi skup bez zadnja 2[/b]? isto tako smo za drugi zadatak moglu odmah kao za prvi reci da nije baza jer ima 5 elemenata a dim=3.
[/quote]
boze :shock: , sta si se ti tu sad proslavio..( :( )
1. ovisi da li te se trazi da reduciras do baze neki skup (neki sistem izvodnica), ili da mozda nadopunjujes linearno nezavisan skup do baze NEKOG PROSTORA
2. ne mozes tako linearno (sablonski) razmisljati(iako i ja nekad znam prebjec na sablonu) :roll: =>ne postoji potpuni algoritam koji ti govori kako rjesavat sve vrste zadataka kao ni za ova tvoja 2!
npr. na ova 2 zadatka mozes napravit bar, ovako od oka gledajuci, 5-6 varijacija razlicitih zadataka, tj. od tvoja 2 napraviti 12 zadataka i da su svi unutar gradiva koje smo obradili 8)
[b]boldano[/b] => zato sto sistem izvodnica mora imati vise ili [b]jednako[/b] elemenata od baze prostora (znaci u 1. >=3, 2.zad >=3)
[quote="Anonymous"]...
dakle, pitanje bi bilo, da li ja nezavisnost, bazu i s.i. odredjujem tek nakon sto sredim skup (izbacim nezavisne) ili odmah na pocetku (kako je rekao prvi primjer).
nadam se da ce netko skuziti sto pitam...
:cry:[/quote]
ovisi sta se trazi u zadatku :twisted:
P.S. ova tvoja dva zadatka(sa tekstom da se trazi baza/sist izv/lin nez za te prostore:
1)odmah se vidi da taj skup nije lin nez u vekt prostoru P2 jer ima 4 elementa sto je >3(broj elemenata prostora P2) => samim time nije ni baza prostora P2
da li je sist izv? => postaviti jednadzbu
2)nije lin nez(skup ima > elemenata od dimenzije prostora) u vekt prostoru R^3 => ako nije lin nez onda nije niti baza prostora R^3
sist izv? postavi jednadzbu =>[color=violet]uoci ova tvoja silna pitanja se uglavnom lome na pitanju da li je sist izvodnica sto se moze traziti na vise nacina[/color][/b]
| Anonymous (napisa): | ...a sto bi bilo da smo izbacili samo 1 polinom i da su nam ostala tri, onda bi trebalo biti baza a mi smo odmah na pocetku rekli da nije...
|
ako bi ta tri koja su ostala bili linearno nezavisni onda bi to znacilo da 3 elementa, linearno nezavisna u prostoru P2 cine BAZU ⇒odmah kad je baza onda je sigurno i sistem izvodnica ZA vekt prostor P2
2. ako se trazi baza/ sist. izv./ lin. nez. u P2 onda ovo gore sta sam rekao stoji!
(uoci boldano  ) )
| Anonymous (napisa): | u drugom zadatku smo prvo izbacili zavisne vektore (zadnja dva) i onda rekli da je baza jer je nezavisan ,a da je skup od kojeg smo krenuli s.i.
zasto smo u prvom zadatku odmah rekli da je lin nezavisan pocetni skup, dok smo u drugom o nezavisnosti razmisljali tek kad smo izbacili one zavisne i dobili novi skup bez zadnja 2? isto tako smo za drugi zadatak moglu odmah kao za prvi reci da nije baza jer ima 5 elemenata a dim=3.
|
boze  , sta si se ti tu sad proslavio..( , sta si se ti tu sad proslavio..(  ) )
1. ovisi da li te se trazi da reduciras do baze neki skup (neki sistem izvodnica), ili da mozda nadopunjujes linearno nezavisan skup do baze NEKOG PROSTORA
2. ne mozes tako linearno (sablonski) razmisljati(iako i ja nekad znam prebjec na sablonu)  ⇒ne postoji potpuni algoritam koji ti govori kako rjesavat sve vrste zadataka kao ni za ova tvoja 2! ⇒ne postoji potpuni algoritam koji ti govori kako rjesavat sve vrste zadataka kao ni za ova tvoja 2!
npr. na ova 2 zadatka mozes napravit bar, ovako od oka gledajuci, 5-6 varijacija razlicitih zadataka, tj. od tvoja 2 napraviti 12 zadataka i da su svi unutar gradiva koje smo obradili 
boldano ⇒ zato sto sistem izvodnica mora imati vise ili jednako elemenata od baze prostora (znaci u 1. >=3, 2.zad >=3)
| Anonymous (napisa): | ...
dakle, pitanje bi bilo, da li ja nezavisnost, bazu i s.i. odredjujem tek nakon sto sredim skup (izbacim nezavisne) ili odmah na pocetku (kako je rekao prvi primjer).
nadam se da ce netko skuziti sto pitam...
 |
ovisi sta se trazi u zadatku 
P.S. ova tvoja dva zadatka(sa tekstom da se trazi baza/sist izv/lin nez za te prostore:
1)odmah se vidi da taj skup nije lin nez u vekt prostoru P2 jer ima 4 elementa sto je >3(broj elemenata prostora P2) ⇒ samim time nije ni baza prostora P2
da li je sist izv? ⇒ postaviti jednadzbu
2)nije lin nez(skup ima > elemenata od dimenzije prostora) u vekt prostoru R^3 ⇒ ako nije lin nez onda nije niti baza prostora R^3
sist izv? postavi jednadzbu ⇒uoci ova tvoja silna pitanja se uglavnom lome na pitanju da li je sist izvodnica sto se moze traziti na vise nacina[/b]
Zadnja promjena: 13_mac; 19:27 sri, 29. 11. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|











