Da post nebude uzaludno iskorišten, rješenje 7. zadatka iz zadaće:
[latex]f\left( x \right) = \sum\limits_{n \ge 0} {\frac{{s_n x^n }}{{n!}}}[/latex]
[latex]s_0 = 1;s_1 = 1;[/latex]
[latex]s_n = s_{n - 1} + \left( {n - 1} \right)s_{n - 2} / \cdot \frac{{x^n }}{{n!}}[/latex]
[latex]\frac{{s_n x^n }}{{n!}} = \frac{{s_{n - 1} x^n }}{{n!}} + \frac{{\left( {n - 1} \right)s_{n - 2} x^n }}{{n!}}/\sum\limits_{n \ge 2} {}[/latex]
[latex]\sum\limits_{n \ge 2} {\frac{{s_n x^n }}{{n!}}} = \sum\limits_{n \ge 2} {\frac{{s_{n - 1} x^n }}{{n!}}} + \sum\limits_{n \ge 2} {\frac{{\left( {n - 1} \right)s_{n - 2} x^n }}{{n!}}}[/latex]
[latex]f\left( x \right) - \frac{{s_1 x^1 }}{{1!}} - \frac{{s_0 x^0 }}{{0!}} = \int {\frac{d}{{dx}}\left( {\sum\limits_{n \ge 2} {\frac{{s_{n - 1} x^n }}{{n!}}} } \right)dx} + \int {\frac{d}{{dx}}\left( {\sum\limits_{n \ge 2} {\frac{{\left( {n - 1} \right)s_{n - 2} x^n }}{{n!}}} } \right)dx}[/latex]
[latex]f\left( x \right) - x - 1 = \int {\left( {\sum\limits_{n \ge 2} {\frac{{n \cdot s_{n - 1} x^{n - 1} }}{{n!}}} } \right)dx} + \int {\left( {\sum\limits_{n \ge 2} {\frac{{n\left( {n - 1} \right)s_{n - 2} x^{n - 1} }}{{n!}}} } \right)dx}[/latex]
[latex]f\left( x \right) - x - 1 = \int {\left( {\sum\limits_{n \ge 2} {\frac{{s_{n - 1} x^{n - 1} }}{{\left( {n - 1} \right)!}}} } \right)dx} + \int {\left( {x\sum\limits_{n \ge 2} {\frac{{s_{n - 2} x^{n - 2} }}{{\left( {n - 2} \right)!}}} } \right)dx}[/latex]
[latex]f\left( x \right) - x - 1 = \int {\left( {f\left( x \right) - \frac{{s_0 x^0 }}{{0!}}} \right)dx} + \int {\left( {x \cdot f\left( x \right)} \right)dx} /\frac{d}{{dx}}[/latex]
[latex]f'\left( x \right) - 1 = f\left( x \right) - 1 + x \cdot f\left( x \right)[/latex]
[latex]\frac{{f'\left( x \right)}}{{f\left( x \right)}} = 1 + x/\int {dx}[/latex]
[latex]\ln \left( {f\left( x \right)} \right) = x + \frac{{x^2 }}{2} + C;x = 0 \Rightarrow f\left( x \right) = \sum\limits_{n \ge 0} {\frac{{s_n \cdot 0^n }}{{n!}}} = s_0 = 1[/latex]
[latex]\ln \left( 1 \right) = 0 + \frac{{0^2 }}{2} + C \Rightarrow C = 0 \Rightarrow f\left( x \right) = e^{x + \frac{{x^2 }}{2}}[/latex]
Da post nebude uzaludno iskorišten, rješenje 7. zadatka iz zadaće:
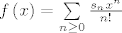
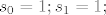
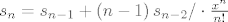
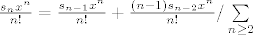
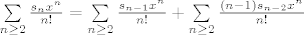

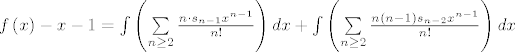
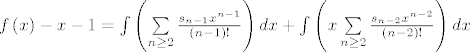
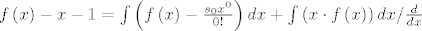
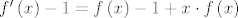
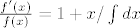
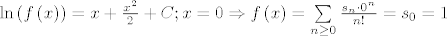
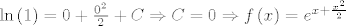
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine










