| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 14:55 pon, 18. 12. 2006 Naslov: Parcijalne i usmjerene derivacije Postano: 14:55 pon, 18. 12. 2006 Naslov: Parcijalne i usmjerene derivacije |
    |
|
|
Def: Neka je [latex]A \subseteq {\bf R}^{\bf n}[/latex] otvoren i [latex]f:A \to {\bf R}^{\bf m}[/latex], te neka je [latex]v \in {\bf R}^{\bf n} ,\left\| v \right\| = 1,c \in A[/latex]. Limes [latex]\mathop {\lim }\limits_{h \to 0} \frac{{f\left( {c + hv} \right) - f\left( c \right)}}{h}[/latex], alo postoji, nazivamo derivacija funkcije [latex]f[/latex] u smjeru vektora [latex]v[/latex] u točki [latex]c[/latex] i označavamo sa [latex]\nabla _v f\left( c \right) = \frac{{\partial f}}{{\partial v}}\left( c \right)[/latex].
Napomena: Neka je [latex]f[/latex] diferencijabilna u [latex]c \in A[/latex]. Tada vrijedi
[latex]\left( 1 \right)\mathop {\lim }\limits_{x \to c} \frac{{\left\| {f\left( x \right) - f\left( c \right) - Df\left( c \right)\left( {x - c} \right)} \right\|}}{{\left\| {x - c} \right\|}}[/latex]
[latex]\left( 2 \right)\mathop {\lim }\limits_{h \to 0} \frac{{\left\| {f\left( {c + hv} \right) - f\left( c \right) - Df\left( c \right)\left( {c + hv - c} \right)} \right\|}}{{\left\| {c + hv - c} \right\|}} = 0[/latex]
[latex]\left( 3 \right)\mathop {\lim }\limits_{h \to 0} \frac{{\left\| {f\left( {c + hv} \right) - f\left( c \right) - hDf\left( c \right)\left( v \right)} \right\|}}{{\left| h \right| \cdot \left\| v \right\|}} = 0[/latex]
[latex]\left( 4 \right)\mathop {\lim }\limits_{h \to 0} \frac{{f\left( {c + hv} \right) - f\left( c \right) - hDf\left( c \right)\left( v \right)}}{h} = 0[/latex]
[latex]\left( 5 \right)\mathop {\lim }\limits_{h \to 0} \left( {\frac{{f\left( {c + hv} \right) - f\left( c \right)}}{h} - Df\left( c \right)\left( v \right)} \right) = 0[/latex]
[latex]\left( 6 \right)\mathop {\lim }\limits_{h \to 0} \frac{{f\left( {c + hv} \right) - f\left( c \right)}}{h} = Df\left( c \right)\left( v \right)[/latex]
[latex]\left( 7 \right)\frac{{\partial f}}{{\partial v}}\left( c \right) = Df\left( c \right)\left( v \right)[/latex].
Uočimo da je usmjerena derivacija poopćenje parcijalne derivacije, jer je [latex]\frac{{\partial f}}{{\partial x_i }}\left( c \right) = Df\left( c \right)\left( {e_i } \right)[/latex].
E, sad ide pitanje. Parcijalne derivacije su bile derivacije skalarnih funkcija, a po ovom što čitam, usmjerena derivacija je derivacija vektorske funkcije. Kak to? I kak smo mogli maknut normu na prijelazu iz (3) u (4) u brojniku?
Def: Neka je 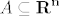 otvoren i otvoren i  , te neka je , te neka je 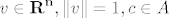 . Limes . Limes 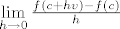 , alo postoji, nazivamo derivacija funkcije , alo postoji, nazivamo derivacija funkcije  u smjeru vektora u smjeru vektora  u točki u točki  i označavamo sa i označavamo sa 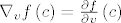 . .
Napomena: Neka je  diferencijabilna u diferencijabilna u 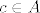 . Tada vrijedi . Tada vrijedi
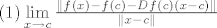
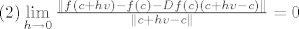
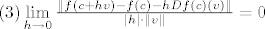
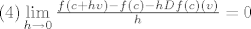
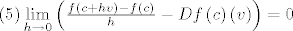
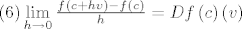
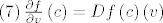 . .
Uočimo da je usmjerena derivacija poopćenje parcijalne derivacije, jer je 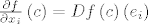 . .
E, sad ide pitanje. Parcijalne derivacije su bile derivacije skalarnih funkcija, a po ovom što čitam, usmjerena derivacija je derivacija vektorske funkcije. Kak to? I kak smo mogli maknut normu na prijelazu iz (3) u (4) u brojniku?
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 16:46 pon, 18. 12. 2006 Naslov: Postano: 16:46 pon, 18. 12. 2006 Naslov: |
    |
|
|
mozes maknut normu zbog svojstva norme da je samo norma nul-vektora nula, pa onda kad norma neceg ide u nulu, ide i ta stvar, znas to kod apsolutnog, sto je poseban slucaj...
a ne znam kak mislis kak to. tak. :D to je promjena u smjeru nekog vektora, ko sto je i parcijalna derivacija, samo sto je tamo jedan specifican vektor, al u principu je ista stvar.
mozes maknut normu zbog svojstva norme da je samo norma nul-vektora nula, pa onda kad norma neceg ide u nulu, ide i ta stvar, znas to kod apsolutnog, sto je poseban slucaj...
a ne znam kak mislis kak to. tak.  to je promjena u smjeru nekog vektora, ko sto je i parcijalna derivacija, samo sto je tamo jedan specifican vektor, al u principu je ista stvar. to je promjena u smjeru nekog vektora, ko sto je i parcijalna derivacija, samo sto je tamo jedan specifican vektor, al u principu je ista stvar.
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 22:02 pon, 18. 12. 2006 Naslov: Postano: 22:02 pon, 18. 12. 2006 Naslov: |
    |
|
|
[quote="Ignavia"]mozes maknut normu zbog svojstva norme da je samo norma nul-vektora nula, pa onda kad norma neceg ide u nulu, ide i ta stvar, znas to kod apsolutnog, sto je poseban slucaj...[/quote]
ok, i mislio sam, znači s desne strane ide nulvektor u 4.
[quote="Ignavia"]a ne znam kak mislis kak to. tak. :D to je promjena u smjeru nekog vektora, ko sto je i parcijalna derivacija, samo sto je tamo jedan specifican vektor, al u principu je ista stvar.[/quote]
Malo me zbunilo to što parcijana dervacija mora biti isključivo od skalarne funkcije. Kod usmjerene mi je jasno da mogu gledat proizvoljan smjer, al sam mislio da će isto bit broj.
Dakle, parcijalne derivacije u točki su brojevi, a usmjerene vektori (mogu bit i vektori u R, znači mogu bit brojevi), jel sam dobro sad skužio?
| Ignavia (napisa): | | mozes maknut normu zbog svojstva norme da je samo norma nul-vektora nula, pa onda kad norma neceg ide u nulu, ide i ta stvar, znas to kod apsolutnog, sto je poseban slucaj... |
ok, i mislio sam, znači s desne strane ide nulvektor u 4.
| Ignavia (napisa): | a ne znam kak mislis kak to. tak.  to je promjena u smjeru nekog vektora, ko sto je i parcijalna derivacija, samo sto je tamo jedan specifican vektor, al u principu je ista stvar. to je promjena u smjeru nekog vektora, ko sto je i parcijalna derivacija, samo sto je tamo jedan specifican vektor, al u principu je ista stvar. |
Malo me zbunilo to što parcijana dervacija mora biti isključivo od skalarne funkcije. Kod usmjerene mi je jasno da mogu gledat proizvoljan smjer, al sam mislio da će isto bit broj.
Dakle, parcijalne derivacije u točki su brojevi, a usmjerene vektori (mogu bit i vektori u R, znači mogu bit brojevi), jel sam dobro sad skužio?
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 22:54 pon, 18. 12. 2006 Naslov: Postano: 22:54 pon, 18. 12. 2006 Naslov: |
    |
|
|
[quote="alen"]
Malo me zbunilo to što parcijana dervacija mora biti isključivo od skalarne funkcije. Kod usmjerene mi je jasno da mogu gledat proizvoljan smjer, al sam mislio da će isto bit broj.
Dakle, parcijalne derivacije u točki su brojevi, a usmjerene vektori (mogu bit i vektori u R, znači mogu bit brojevi), jel sam dobro sad skužio?[/quote]
parcijalna derivacija ne mora biti od skalarne funkcije.
ovako, imas derivaciju u smjeru nekog vektora - znaci to moze biti bilo koji vektor, pa onda ako je duz vektora e_i, onda je to parcijalna derivacija.
i kada imas vektorske funkcije, onda su ti parcijalne derivacije i sve ostale derivacije u smjeru vektori.
| alen (napisa): |
Malo me zbunilo to što parcijana dervacija mora biti isključivo od skalarne funkcije. Kod usmjerene mi je jasno da mogu gledat proizvoljan smjer, al sam mislio da će isto bit broj.
Dakle, parcijalne derivacije u točki su brojevi, a usmjerene vektori (mogu bit i vektori u R, znači mogu bit brojevi), jel sam dobro sad skužio? |
parcijalna derivacija ne mora biti od skalarne funkcije.
ovako, imas derivaciju u smjeru nekog vektora - znaci to moze biti bilo koji vektor, pa onda ako je duz vektora e_i, onda je to parcijalna derivacija.
i kada imas vektorske funkcije, onda su ti parcijalne derivacije i sve ostale derivacije u smjeru vektori.
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 23:17 pon, 18. 12. 2006 Naslov: Postano: 23:17 pon, 18. 12. 2006 Naslov: |
    |
|
|
[quote="Ignavia"]
parcijalna derivacija ne mora biti od skalarne funkcije.
ovako, imas derivaciju u smjeru nekog vektora - znaci to moze biti bilo koji vektor, pa onda ako je duz vektora e_i, onda je to parcijalna derivacija.
i kada imas vektorske funkcije, onda su ti parcijalne derivacije i sve ostale derivacije u smjeru vektori.[/quote]
Izgleda da imamo problem:
Like ordinary derivatives, the partial derivative is defined as a limit. Let U be an open subset of Rn and f : U → R a function. We define the partial derivative of f at the point a = (a1, ..., an) ∈ U with respect to the i-th variable xi as [latex]\frac{\partial }{{\partial x_i }}f\left( {a_1 ,...,a_n } \right)\mathop = {\lim }\limits_{h \to 0} \frac{{f\left( {a_1 ,...,a_{i - 1} ,a_i + h,a_{i + 1} ,...,a_n } \right) - f\left( {a_1 ,...,a_n } \right)}}{h}[/latex] (na wikipediji).
Def(predavanja): Parcijalne derivacije fukcije f u točki c iz A (A je otvoren i domena funkcije f) dane su sa [latex]\frac{\partial }{{\partial x_j }}f_i \left( c \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f_i \left( {c_1 ,...,c_{j - 1} ,c_j + h,c_{j + 1} ,...,c_n } \right) - f_i \left( {c_1 ,...,c_n } \right)}}{h}[/latex]
| Ignavia (napisa): |
parcijalna derivacija ne mora biti od skalarne funkcije.
ovako, imas derivaciju u smjeru nekog vektora - znaci to moze biti bilo koji vektor, pa onda ako je duz vektora e_i, onda je to parcijalna derivacija.
i kada imas vektorske funkcije, onda su ti parcijalne derivacije i sve ostale derivacije u smjeru vektori. |
Izgleda da imamo problem:
Like ordinary derivatives, the partial derivative is defined as a limit. Let U be an open subset of Rn and f : U → R a function. We define the partial derivative of f at the point a = (a1, ..., an) ∈ U with respect to the i-th variable xi as 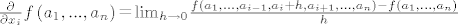 (na wikipediji). (na wikipediji).
Def(predavanja): Parcijalne derivacije fukcije f u točki c iz A (A je otvoren i domena funkcije f) dane su sa 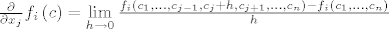
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 23:22 pon, 18. 12. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 23:22 pon, 18. 12. 2006 Naslov: Postano: 23:22 pon, 18. 12. 2006 Naslov: |
    |
|
|
prof. Ungar, Matematicka analiza 3, str 70.:
"U definiciji derivacije duž vektora i parcijalnih derivacija, nije bilo nužno da se radi o realnoj funkciji. Na potpuno isti način definiraju se ti pojmovi i za vektorske funkcije, samo što to sada neće biti brojevi, nego vektori."
kad meni vec ne vjerujes... :lol:
prof. Ungar, Matematicka analiza 3, str 70.:
"U definiciji derivacije duž vektora i parcijalnih derivacija, nije bilo nužno da se radi o realnoj funkciji. Na potpuno isti način definiraju se ti pojmovi i za vektorske funkcije, samo što to sada neće biti brojevi, nego vektori."
kad meni vec ne vjerujes... 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 23:23 pon, 18. 12. 2006 Naslov: Postano: 23:23 pon, 18. 12. 2006 Naslov: |
    |
|
|
ma vjerujem ti, al mi nije jasno :cry:
ok, sad je
al zašt imamo takvu definiciju? :shock: to je sadizam 8)
namjerno nas žele zbunit
aha, znači, možda će i nama tak reć da to moežmo i s vektorima... al kak smo onda već usmjerenu... da bar stave predavanja uskoro na net
ma vjerujem ti, al mi nije jasno 
ok, sad je
al zašt imamo takvu definiciju?  to je sadizam to je sadizam 
namjerno nas žele zbunit
aha, znači, možda će i nama tak reć da to moežmo i s vektorima... al kak smo onda već usmjerenu... da bar stave predavanja uskoro na net
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 23:25 pon, 18. 12. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 23:26 pon, 18. 12. 2006 Naslov: Postano: 23:26 pon, 18. 12. 2006 Naslov: |
    |
|
|
[quote="mdoko"][quote="alen"]
Def(predavanja): Parcijalne derivacija fukcije f u točki c iz A (A je otvoren i domena funkcije f) dane su sa [latex]\frac{\partial }{{\partial x_j }}f_i \left( c \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f_i \left( {c_1 ,...,c_{i - 1} ,c_i + h,c_{i + 1} ,...,c_n } \right) - f_i \left( {c_1 ,...,c_n } \right)}}{h}[/latex][/quote]
Dobro. I zasto ti kodomena funkcije [latex]f_i[/latex] ne moze biti [latex]\mathbb{R}^n[/latex] za neki [latex]n>1[/latex].[/quote]
f_i smo definirali kao koordinatne funkcije, to jest, realne funkcije više varijabli.
| mdoko (napisa): | | alen (napisa): |
Def(predavanja): Parcijalne derivacija fukcije f u točki c iz A (A je otvoren i domena funkcije f) dane su sa 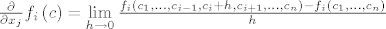 |
Dobro. I zasto ti kodomena funkcije 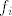 ne moze biti ne moze biti  za neki za neki 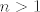 . . |
f_i smo definirali kao koordinatne funkcije, to jest, realne funkcije više varijabli.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 23:37 pon, 18. 12. 2006 Naslov: Postano: 23:37 pon, 18. 12. 2006 Naslov: |
    |
|
|
[quote="alen"]
f_i smo definirali kao koordinatne funkcije, to jest, realne funkcije više varijabli.[/quote]
OK, ali u definiciji
[latex]\frac{\partial }{{\partial x_i }}f \left( c \right) := \mathop {\lim }\limits_{h \to 0} \frac{{f \left( {c_1 ,...,c_{i - 1} ,c_i + h,c_{i + 1} ,...,c_n } \right) - f \left( {c_1 ,...,c_n } \right)}}{h}[/latex], sto te sprecava da [latex]f[/latex] bude vektorska funkcija?
| alen (napisa): |
f_i smo definirali kao koordinatne funkcije, to jest, realne funkcije više varijabli. |
OK, ali u definiciji
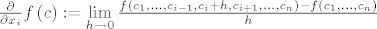 , sto te sprecava da , sto te sprecava da  bude vektorska funkcija? bude vektorska funkcija?
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 23:43 pon, 18. 12. 2006 Naslov: Postano: 23:43 pon, 18. 12. 2006 Naslov: |
    |
|
|
[quote="alen"]e, hvala, mislim da će pomoć, nisam znao da ima :oops:
stvarno puno hvala[/quote]
nema na cemu, pomogla bi i crnom ciganu :lol:
salim se, tj ne, al drago mi je da si sretan i uvijek sam tu za tebe :cmok: :dodji:
| alen (napisa): | e, hvala, mislim da će pomoć, nisam znao da ima 
stvarno puno hvala |
nema na cemu, pomogla bi i crnom ciganu 
salim se, tj ne, al drago mi je da si sretan i uvijek sam tu za tebe  
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 23:58 pon, 18. 12. 2006 Naslov: Postano: 23:58 pon, 18. 12. 2006 Naslov: |
    |
|
|
[quote="mdoko"][quote="alen"]
f_i smo definirali kao koordinatne funkcije, to jest, realne funkcije više varijabli.[/quote]
OK, ali u definiciji
[latex]\frac{\partial }{{\partial x_i }}f \left( c \right) := \mathop {\lim }\limits_{h \to 0} \frac{{f \left( {c_1 ,...,c_{i - 1} ,c_i + h,c_{i + 1} ,...,c_n } \right) - f \left( {c_1 ,...,c_n } \right)}}{h}[/latex], sto te sprecava da [latex]f[/latex] bude vektorska funkcija?[/quote]
Let U be an open subset of Rn and f : U → R a function. (možda ja jedini tak to doživljavam, al meni se to čini dost ograničavajuće u tom smislu)
Aha, sad sam skužio, sry. Pa koordinatne funkcije nam po definiciji skalarne funkcije.
E, al izvuko si pola definicije iz wikipedije za koju piše "Let U be an open subset of Rn and f : U → R a function." , a drugu polovicu iz definicije s predavanja.
| mdoko (napisa): | | alen (napisa): |
f_i smo definirali kao koordinatne funkcije, to jest, realne funkcije više varijabli. |
OK, ali u definiciji
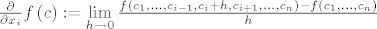 , sto te sprecava da , sto te sprecava da  bude vektorska funkcija? bude vektorska funkcija? |
Let U be an open subset of Rn and f : U → R a function. (možda ja jedini tak to doživljavam, al meni se to čini dost ograničavajuće u tom smislu)
Aha, sad sam skužio, sry. Pa koordinatne funkcije nam po definiciji skalarne funkcije.
E, al izvuko si pola definicije iz wikipedije za koju piše "Let U be an open subset of Rn and f : U → R a function." , a drugu polovicu iz definicije s predavanja.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 3:49 uto, 19. 12. 2006 Naslov: Postano: 3:49 uto, 19. 12. 2006 Naslov: |
    |
|
|
[quote="Ignavia"]prof. Ungar, Matematicka analiza 3, str 70.:
"U definiciji derivacije duž vektora i parcijalnih derivacija, nije bilo nužno da se radi o realnoj funkciji. Na potpuno isti način definiraju se ti pojmovi i za vektorske funkcije, samo što to sada neće biti brojevi, nego vektori."[/quote]
:OT: Kao da citam religijsku raspravu gdje se netko poziva na Bibliju... :lol:
| Ignavia (napisa): | prof. Ungar, Matematicka analiza 3, str 70.:
"U definiciji derivacije duž vektora i parcijalnih derivacija, nije bilo nužno da se radi o realnoj funkciji. Na potpuno isti način definiraju se ti pojmovi i za vektorske funkcije, samo što to sada neće biti brojevi, nego vektori." |
 Kao da citam religijsku raspravu gdje se netko poziva na Bibliju... Kao da citam religijsku raspravu gdje se netko poziva na Bibliju... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
|














