| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 21:40 pon, 9. 10. 2006 Naslov: Postano: 21:40 pon, 9. 10. 2006 Naslov: |
    |
|
|
Demonstrature iz LA1 [color=red]se budu održavale[/color] petkom od 14:00 do 16:00. Ako nitko ne dođe u prvih 15 minuta, ja [color=red]sam bio otišao jest[/color] i onda ništ od demonstratura.
Okupljanje pred oglasnom pločom, [color=red]bijah[/color] tamo, [color=red]bih počeo[/color] 6.10., znači ovaj petak.
Nadam se da [color=red]neka netko dođe[/color].
Ako nitko ne dođe do 14:15, ja [size=18]bijah otišao [color=red]JEST[/color][/size]
Pozdrav.
Alen Lančić
P.S. Hvala kolegici nani na uočenoj grešci i predloženom ispravku, ovako mi se puno više sviđa.
Demonstrature iz LA1 se budu održavale petkom od 14:00 do 16:00. Ako nitko ne dođe u prvih 15 minuta, ja sam bio otišao jest i onda ništ od demonstratura.
Okupljanje pred oglasnom pločom, bijah tamo, bih počeo 6.10., znači ovaj petak.
Nadam se da neka netko dođe.
Ako nitko ne dođe do 14:15, ja bijah otišao JEST
Pozdrav.
Alen Lančić
P.S. Hvala kolegici nani na uočenoj grešci i predloženom ispravku, ovako mi se puno više sviđa.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 22:41 pet, 27. 10. 2006 Naslov: Postano: 22:41 pet, 27. 10. 2006 Naslov: |
    |
|
|
Evo, dragi moji linearci. Danas me cijenjena kolegica sa prve godine pitala ovakvo pitanje (ne sjećam se brojeva točno):
Neka je operator zadan sa [latex]T = \left[ {\begin{array}{*{20}c}
6 & 7 \\
{ - 4} & { - 4} \\
\end{array}} \right][/latex] u bazi [latex]a = \left[ \begin{array}{l}
1 \\
1 \\
\end{array} \right][/latex], [latex]b = \left[ \begin{array}{l}
2 \\
1 \\
\end{array} \right][/latex]. Treba naći djelovanje operatora u bazi [latex]\left\{ {\left[ \begin{array}{l}
1 \\
0 \\
\end{array} \right],\left[ \begin{array}{l}
0 \\
1 \\
\end{array} \right]} \right\}[/latex].
Dakle, kolegica je to riješila ovako:
[latex]b - a = \left[ {\begin{array}{*{20}c}
1 \\
0 \\
\end{array}} \right][/latex], [latex]2a - b = \left[ {\begin{array}{*{20}c}
0 \\
1 \\
\end{array}} \right][/latex], [latex]T\left( a \right) = \left[ {\begin{array}{*{20}c}
6 & 7 \\
{ - 4} & { - 4} \\
\end{array}} \right]\left[ {\begin{array}{*{20}c}
1 \\
0 \\
\end{array}} \right] = \left[ {\begin{array}{*{20}c}
6 \\
{ - 4} \\
\end{array}} \right][/latex], [latex]T\left( b \right) = \left[ {\begin{array}{*{20}c}
6 & 7 \\
{ - 4} & { - 4} \\
\end{array}} \right]\left[ {\begin{array}{*{20}c}
0 \\
1 \\
\end{array}} \right] = \left[ {\begin{array}{*{20}c}
7 \\
{ - 4} \\
\end{array}} \right][/latex].
E, sad [latex]T\left( {b - a} \right) = T\left( b \right) - T\left( a \right) = a
[/latex], [latex]T\left( {2a - b} \right) = 2T\left( a \right) - T\left( b \right) = 5a - 4b[/latex]. Znači da u kanonskoj bazi operator djeluje ovako [latex]T\left[ \begin{array}{l}
1 \\
0 \\
\end{array} \right] = \left[ \begin{array}{l}
1 \\
1 \\
\end{array} \right][/latex], [latex]T\left[ \begin{array}{l}
0 \\
1 \\
\end{array} \right] = \left[ {\begin{array}{*{20}c}
{ - 3} \\
1 \\
\end{array}} \right][/latex]. Operator ima prikaz u kanonskoj bazi [latex]T = \left[ {\begin{array}{*{20}c}
1 & { - 3} \\
1 & 1 \\
\end{array}} \right][/latex]
I sad ja razmišljam, mi smo to radili u drugom semestru sa izomorfizmom mat. Ovo mi se više čini kao učenje postupka napamet, nego razumjevanje gradiva (ovo je primjedba rasporedu programa, a ne kolegici, koja me zadivila svojim načinom razmišljanja).
Volio bih da sam to mogao objasniti ovako:
Matrica prijelaza iz (a,b) u (i,j) je [latex]P = \left[ {\begin{array}{*{20}c}
1 & 2 \\
1 & 1 \\
\end{array}} \right][/latex], iz (i,j) u (a,b) je [latex]P^{ - 1} = \left[ {\begin{array}{*{20}c}
{ - 1} & 2 \\
1 & { - 1} \\
\end{array}} \right][/latex]. Zadana je matrica operatora[latex]B = \left[ {\begin{array}{*{20}c}
6 & 7 \\
{ - 4} & { - 4} \\
\end{array}} \right][/latex] pa je matrica operatora u kanonskoj bazi [latex]A = PBP^{ - 1}[/latex] (uz nacrtanu sliku).
Antonićev redoslijed gradiva je zakon.
Evo, dragi moji linearci. Danas me cijenjena kolegica sa prve godine pitala ovakvo pitanje (ne sjećam se brojeva točno):
Neka je operator zadan sa 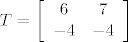 u bazi u bazi 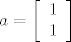 , , 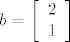 . Treba naći djelovanje operatora u bazi . Treba naći djelovanje operatora u bazi  . .
Dakle, kolegica je to riješila ovako:
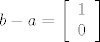 , , 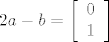 , , 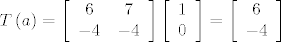 , , 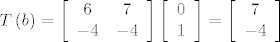 . .
E, sad 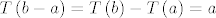 , , 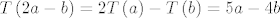 . Znači da u kanonskoj bazi operator djeluje ovako . Znači da u kanonskoj bazi operator djeluje ovako 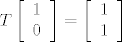 , ,  . Operator ima prikaz u kanonskoj bazi . Operator ima prikaz u kanonskoj bazi 
I sad ja razmišljam, mi smo to radili u drugom semestru sa izomorfizmom mat. Ovo mi se više čini kao učenje postupka napamet, nego razumjevanje gradiva (ovo je primjedba rasporedu programa, a ne kolegici, koja me zadivila svojim načinom razmišljanja).
Volio bih da sam to mogao objasniti ovako:
Matrica prijelaza iz (a,b) u (i,j) je 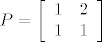 , iz (i,j) u (a,b) je , iz (i,j) u (a,b) je 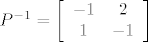 . Zadana je matrica operatora . Zadana je matrica operatora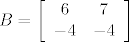 pa je matrica operatora u kanonskoj bazi pa je matrica operatora u kanonskoj bazi 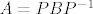 (uz nacrtanu sliku). (uz nacrtanu sliku).
Antonićev redoslijed gradiva je zakon.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
vanja
Forumaš(ica)


Pridružen/a: 16. 02. 2006. (16:38:26)
Postovi: (9E)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
vanja
Forumaš(ica)


Pridružen/a: 16. 02. 2006. (16:38:26)
Postovi: (9E)16
Spol: 
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
ft
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (21:38:47)
Postovi: (25)16
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 22:08 ned, 21. 10. 2007 Naslov: Postano: 22:08 ned, 21. 10. 2007 Naslov: |
    |
|
|
Željko Kereta i Rafael Mrđen drže demonstrature ponedjeljkom 16:00-18:00.
Prvih 15 min svakog sata ćemo biti ispred oglasne, a kasnije u knjižnici ili nekom od praktikuma.
EDIT: promjena plana, prvo nas potrazite u 105. ako nije slobodna (a vjerojatno ce biti, jer je bila prekjucer) onda smo ispred oglasne. vrijedi od [latex]H^{00}-H^{15}, H \in \{16,17\}[/latex]
Željko Kereta i Rafael Mrđen drže demonstrature ponedjeljkom 16:00-18:00.
Prvih 15 min svakog sata ćemo biti ispred oglasne, a kasnije u knjižnici ili nekom od praktikuma.
EDIT: promjena plana, prvo nas potrazite u 105. ako nije slobodna (a vjerojatno ce biti, jer je bila prekjucer) onda smo ispred oglasne. vrijedi od 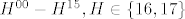
_________________
Rafael Mrđen
Zadnja promjena: rafaelm; 22:15 sri, 24. 10. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
 Postano: 22:47 ned, 21. 10. 2007 Naslov: Postano: 22:47 ned, 21. 10. 2007 Naslov: |
    |
|
|
Zrinka Draškić i Iva Kasum držat će demonstrature iz Linearne algebre srijedom od 13 do 15 sati, u učionici 105. Sigurno ćemo tamo biti 13:00-13:15 i 14:00-14:15, pa se oni koji imaju nastavu do 14 i žele doći nakon toga ne moraju posebno najavljivati :) Ako netko misli doći nakon tih 15 minuta svakog sata, bilo bi lijepo da nekako to javi, na mail ili pm... Sigurno smo na faxu, samo možda nećemo cijelo vrijeme biti u 105, pa da se ne tražimo po faxu :) Ako kojim slučajem 105 bude zauzeta u to vrijeme, onda čekamo ispred oglasne ploče prvih 15 minuta svakog sata.
Zrinka Draškić i Iva Kasum držat će demonstrature iz Linearne algebre srijedom od 13 do 15 sati, u učionici 105. Sigurno ćemo tamo biti 13:00-13:15 i 14:00-14:15, pa se oni koji imaju nastavu do 14 i žele doći nakon toga ne moraju posebno najavljivati  Ako netko misli doći nakon tih 15 minuta svakog sata, bilo bi lijepo da nekako to javi, na mail ili pm... Sigurno smo na faxu, samo možda nećemo cijelo vrijeme biti u 105, pa da se ne tražimo po faxu Ako netko misli doći nakon tih 15 minuta svakog sata, bilo bi lijepo da nekako to javi, na mail ili pm... Sigurno smo na faxu, samo možda nećemo cijelo vrijeme biti u 105, pa da se ne tražimo po faxu  Ako kojim slučajem 105 bude zauzeta u to vrijeme, onda čekamo ispred oglasne ploče prvih 15 minuta svakog sata. Ako kojim slučajem 105 bude zauzeta u to vrijeme, onda čekamo ispred oglasne ploče prvih 15 minuta svakog sata.
_________________ kalendar 
  |
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
 Postano: 22:12 sub, 17. 11. 2007 Naslov: Postano: 22:12 sub, 17. 11. 2007 Naslov: |
    |
|
|
u sljedeća dva kolokvijska tjedna neće biti demonstratura u redovnom terminu, nego po dogovoru... dakle, ak netko želi doć na demonstrature, neka se javi na mail ili pm, pa se dogovorimo za neki termin... ako netko ima samo jedno pitanje ili tako nešto, može to pitati i preko maila ili pm-a :)
u sljedeća dva kolokvijska tjedna neće biti demonstratura u redovnom terminu, nego po dogovoru... dakle, ak netko želi doć na demonstrature, neka se javi na mail ili pm, pa se dogovorimo za neki termin... ako netko ima samo jedno pitanje ili tako nešto, može to pitati i preko maila ili pm-a 
_________________ kalendar 
  |
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
|
















