| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
marijap
Forumaš(ica)


Pridružen/a: 21. 06. 2006. (19:04:40)
Postovi: (209)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
jakov
Forumaš(ica)

Pridružen/a: 30. 08. 2006. (20:03:41)
Postovi: (47)16
Spol: 
Lokacija: evo me doma
|
 Postano: 19:48 sub, 6. 1. 2007 Naslov: Postano: 19:48 sub, 6. 1. 2007 Naslov: |
    |
|
|
Ne budimo lijeni pa ih prebrojimo zajedno: 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Ukupno 21. (vičite ako koji nedostaje ili pak je viška)
Ne budimo lijeni pa ih prebrojimo zajedno: 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Ukupno 21. (vičite ako koji nedostaje ili pak je viška)
|
|
| [Vrh] |
|
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
 Postano: 21:58 sub, 6. 1. 2007 Naslov: Postano: 21:58 sub, 6. 1. 2007 Naslov: |
    |
|
|
[quote="jakov"]Ne budimo lijeni pa ih prebrojimo zajedno: 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Ukupno 21. (vičite ako koji nedostaje ili pak je viška)[/quote]
mislim da je sve ok.
| jakov (napisa): | Ne budimo lijeni pa ih prebrojimo zajedno: 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Ukupno 21. (vičite ako koji nedostaje ili pak je viška) |
mislim da je sve ok.
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
 Postano: 22:09 sub, 6. 1. 2007 Naslov: Postano: 22:09 sub, 6. 1. 2007 Naslov: |
    |
|
|
[quote="jakov"]Ne budimo lijeni pa ih prebrojimo zajedno: 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Ukupno 21. (vičite ako koji nedostaje ili pak je viška)[/quote]
imas pravo, moja greska, ja stavio i 91 :oops: :oops: :oops: :oops: :oops:
| jakov (napisa): | Ne budimo lijeni pa ih prebrojimo zajedno: 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Ukupno 21. (vičite ako koji nedostaje ili pak je viška) |
imas pravo, moja greska, ja stavio i 91     
_________________
Everybody Dies...
Nobody is perfect...
Non scholae, sed vitae discimus
|
|
| [Vrh] |
|
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
marijap
Forumaš(ica)


Pridružen/a: 21. 06. 2006. (19:04:40)
Postovi: (209)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
Mighty Beaver
Forumaš(ica)

Pridružen/a: 14. 12. 2005. (19:57:26)
Postovi: (A)16
|
|
| [Vrh] |
|
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
 Postano: 23:02 pon, 8. 1. 2007 Naslov: Postano: 23:02 pon, 8. 1. 2007 Naslov: |
    |
|
|
[quote="Mighty Beaver"]da pitam nesto oko 7 zad... vidim da ste vise manje svi dobili isto ali ja sam ga pokusao rijesiti ovako i ne vidim sto je tu krivo pa pomozite...
dakle:
na prvom katu ih izide a, na drugom b ... na zadnjem e.
a+b+c+d+e=8
jos imamo uvijet da je svaki a,b..,e veci od 0 (jer na svakom mora netko izaci).
sto tu ne valja?
hvala.[/quote]
nije da puno znam o tome,ali...
mislim da bi po ovom nacinu trebalo postaviti ogranicenje i odozgora,jer moze izaci vise od 1 covjek,ali nisi ogranicio ali ne vise od 4ljudi.
ali to je samo moje misljenje.:?
moj savjet-probaj direktno sa fui bez jednadzbi.
| Mighty Beaver (napisa): | da pitam nesto oko 7 zad... vidim da ste vise manje svi dobili isto ali ja sam ga pokusao rijesiti ovako i ne vidim sto je tu krivo pa pomozite...
dakle:
na prvom katu ih izide a, na drugom b ... na zadnjem e.
a+b+c+d+e=8
jos imamo uvijet da je svaki a,b..,e veci od 0 (jer na svakom mora netko izaci).
sto tu ne valja?
hvala. |
nije da puno znam o tome,ali...
mislim da bi po ovom nacinu trebalo postaviti ogranicenje i odozgora,jer moze izaci vise od 1 covjek,ali nisi ogranicio ali ne vise od 4ljudi.
ali to je samo moje misljenje.
moj savjet-probaj direktno sa fui bez jednadzbi.
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 23:04 pon, 8. 1. 2007 Naslov: Postano: 23:04 pon, 8. 1. 2007 Naslov: |
    |
|
|
Ako ljudima damo imena A, B, C, D, E, F, G i H, da li si uzeo u obzir da nije isto ako izadju (grupirano po katovima) ABCD/E/F/G/H i HBCD/E/F/G/A (tj. bitno je i tko gdje izadje, a ne samo koliko ljudi)? :-k
Isprika ako sam fulao o kojem je zadatku rijec. :)
Ako ljudima damo imena A, B, C, D, E, F, G i H, da li si uzeo u obzir da nije isto ako izadju (grupirano po katovima) ABCD/E/F/G/H i HBCD/E/F/G/A (tj. bitno je i tko gdje izadje, a ne samo koliko ljudi)? 
Isprika ako sam fulao o kojem je zadatku rijec. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
vanja
Forumaš(ica)


Pridružen/a: 16. 02. 2006. (16:38:26)
Postovi: (9E)16
Spol: 
|
 Postano: 11:13 uto, 9. 1. 2007 Naslov: Postano: 11:13 uto, 9. 1. 2007 Naslov: |
    |
|
|
[b]7. zadatak[/b]: za dogadjaje [latex] A_i [/latex] stavis {nitko nije izasao na i-tom katu}, i=1,2,3,4,5 ,
kardinalni broj od svakog [latex] A_i [/latex] lako izracunas, a u zadatku se upravo trazi kardinalni broj od PRESJEKA KOMPLEMENATA (tj barem netko je izisao na prvom katu I barem netko na drugom I .... I barem netko je izisao na petom katu) -to naravno ides po FUI gdje je onaj osnovni skup S={8-ero ljudi izlazi proizvoljno na 5 katova} i kardinalni od S je naravno [latex] 5^8 [/latex]
7. zadatak: za dogadjaje 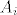 stavis {nitko nije izasao na i-tom katu}, i=1,2,3,4,5 , stavis {nitko nije izasao na i-tom katu}, i=1,2,3,4,5 ,
kardinalni broj od svakog 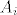 lako izracunas, a u zadatku se upravo trazi kardinalni broj od PRESJEKA KOMPLEMENATA (tj barem netko je izisao na prvom katu I barem netko na drugom I .... I barem netko je izisao na petom katu) -to naravno ides po FUI gdje je onaj osnovni skup S={8-ero ljudi izlazi proizvoljno na 5 katova} i kardinalni od S je naravno lako izracunas, a u zadatku se upravo trazi kardinalni broj od PRESJEKA KOMPLEMENATA (tj barem netko je izisao na prvom katu I barem netko na drugom I .... I barem netko je izisao na petom katu) -to naravno ides po FUI gdje je onaj osnovni skup S={8-ero ljudi izlazi proizvoljno na 5 katova} i kardinalni od S je naravno 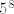
|
|
| [Vrh] |
|
Mighty Beaver
Forumaš(ica)

Pridružen/a: 14. 12. 2005. (19:57:26)
Postovi: (A)16
|
|
| [Vrh] |
|
SvekY
Forumaš(ica)


Pridružen/a: 21. 11. 2003. (23:44:22)
Postovi: (FF)16
Spol: 
Lokacija: unitarni vektorski prostor
|
 Postano: 2:16 sri, 10. 1. 2007 Naslov: Postano: 2:16 sri, 10. 1. 2007 Naslov: |
    |
|
|
Pitanje za [b]8. zadatak[/b]:
[u]1. pokušaj[/u]: Kada sam shvatio da "Marko sa svakim parom večera 6 puta" znači da, na primjer, sa 2. i 6. prijateljem (a možda i još s nekim) večera 6 puta, to sam zapisao ovako:
[latex]| A_2 \cap A_6 | = 6[/latex], ustvari, [latex]|A_i \cap A_j| = 6, \forall i \ne j[/latex]
Pomoću FUI sam našao [latex]| \bigcup A_i |[/latex] i zbrojio sa brojem večera bez društva [latex]| (\bigcup A_i)^c |[/latex], te dobio ukupan broj večera.
To sam ja htio, ali već FUIjem sam dobio da je [latex]| \bigcup A_i |<0[/latex] točnije jednako -8.
[u]2. pokušaj[/u]: Pokušao sam "Marko sa svakim parom večera 6 puta" shvatiti i ovako: On večera sa samo 2 prijatelja i nikim drugim. to znači da umjesto alterirajućih prednznaka kao u FUI, dobivam sve "+".
U tom slučaju dobivam konačno rješenje sve skupa 272!!
:?
Kako ste vi sa rezultatom 36 (tj. svi koji su ovdje zapisali rezultate), shvatili zadatak?
Ništa drugo mi ne pad na pamet, a mislim da mi je sve točno u računu.
Help! :puppydogeyes:
Pitanje za 8. zadatak:
1. pokušaj: Kada sam shvatio da "Marko sa svakim parom večera 6 puta" znači da, na primjer, sa 2. i 6. prijateljem (a možda i još s nekim) večera 6 puta, to sam zapisao ovako:
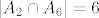 , ustvari, , ustvari, 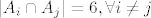
Pomoću FUI sam našao 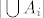 i zbrojio sa brojem večera bez društva i zbrojio sa brojem večera bez društva 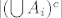 , te dobio ukupan broj večera. , te dobio ukupan broj večera.
To sam ja htio, ali već FUIjem sam dobio da je 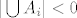 točnije jednako -8. točnije jednako -8.
2. pokušaj: Pokušao sam "Marko sa svakim parom večera 6 puta" shvatiti i ovako: On večera sa samo 2 prijatelja i nikim drugim. to znači da umjesto alterirajućih prednznaka kao u FUI, dobivam sve "+".
U tom slučaju dobivam konačno rješenje sve skupa 272!!

Kako ste vi sa rezultatom 36 (tj. svi koji su ovdje zapisali rezultate), shvatili zadatak?
Ništa drugo mi ne pad na pamet, a mislim da mi je sve točno u računu.
Help! 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 12:10 sri, 10. 1. 2007 Naslov: Postano: 12:10 sri, 10. 1. 2007 Naslov: |
    |
|
|
12 puta je bio s prvim
12 puta je bio s drugim
...
12 puta je bio sa šestim prijateljem
6 puta sa prvim i drugim
6 puta sa prvim i trećim...
Ak ti je lakše, nacrtaj si 6 krugova, u svakom treba bit po 12 točaka, u presjeku svaka dva treba bit 6 točaka, svaka tri treba bit 4 točke... i u presjeku svih 1 točka. Kreneš od ove jedne koja je u presjeku svih krugova, onda dodaš još po točku u svaki presjek od točno 5 krugova da bi u svakom takvom presjeku bilo po 2 točke, onda dodaš još po jednu u svaki presjek od točno 4 kruga tak da u svakom takvom presjeku imaš 3 točke itd. Još na kraju nacrtaš 8 točaka izvan svih krugova. Sad uzmeš da ti je papir na kojem si crto univerzalni skup i trebaš prebrojat kolko točaka sadrži. To je broj Markovih izlazaka.
12 puta je bio s prvim
12 puta je bio s drugim
...
12 puta je bio sa šestim prijateljem
6 puta sa prvim i drugim
6 puta sa prvim i trećim...
Ak ti je lakše, nacrtaj si 6 krugova, u svakom treba bit po 12 točaka, u presjeku svaka dva treba bit 6 točaka, svaka tri treba bit 4 točke... i u presjeku svih 1 točka. Kreneš od ove jedne koja je u presjeku svih krugova, onda dodaš još po točku u svaki presjek od točno 5 krugova da bi u svakom takvom presjeku bilo po 2 točke, onda dodaš još po jednu u svaki presjek od točno 4 kruga tak da u svakom takvom presjeku imaš 3 točke itd. Još na kraju nacrtaš 8 točaka izvan svih krugova. Sad uzmeš da ti je papir na kojem si crto univerzalni skup i trebaš prebrojat kolko točaka sadrži. To je broj Markovih izlazaka.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
SvekY
Forumaš(ica)


Pridružen/a: 21. 11. 2003. (23:44:22)
Postovi: (FF)16
Spol: 
Lokacija: unitarni vektorski prostor
|
|
| [Vrh] |
|
vedraf
Forumaš(ica)

Pridružen/a: 18. 09. 2006. (15:47:50)
Postovi: (BB)16
|
|
| [Vrh] |
|
SvekY
Forumaš(ica)


Pridružen/a: 21. 11. 2003. (23:44:22)
Postovi: (FF)16
Spol: 
Lokacija: unitarni vektorski prostor
|
|
| [Vrh] |
|
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
|















