| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 17:10 ned, 14. 1. 2007 Naslov: diferencijabilnost Postano: 17:10 ned, 14. 1. 2007 Naslov: diferencijabilnost |
    |
|
|
U realnom slučaju vrijedila je sljedeća karakterizacija diferencijabilnosti u točki:
Neka je [latex]f:I \to {\bf R}[/latex] funkcija. Tada je [latex]f[/latex] derivabilna u [latex]c[/latex] akko postoje [latex]A \in {\bf R}[/latex] i [latex]\omega :I \to {\bf R}[/latex] takva da [latex]\mathop {\lim }\limits_{x \to c} \omega \left( {x - c} \right) = 0[/latex] takvi da je [latex]f\left( x \right) - f\left( c \right) = A \cdot \left( {x - c} \right) + \left( {x - c} \right) \cdot \omega \left( {x - c} \right),\forall x \in I[/latex]. Štoviše, tada je [latex]f'\left( c \right) = A[/latex].
E sada, uzimajući u obzir tu karakterizaciju i ono što je asistentica Hanzer rekla na vježbama: Funkcija je diferencijabilna u c pa možemo napisati [latex]f\left( x \right) - f\left( c \right) = ''{\rm nesto linearno'' + ''nesto malo''}[/latex], zanima me što bi formalno bilo to "nešto malo", a za ovo nešto linearno mi se čini dosta jasno da je to diferencijal od f u c.
U realnom slučaju vrijedila je sljedeća karakterizacija diferencijabilnosti u točki:
Neka je  funkcija. Tada je funkcija. Tada je  derivabilna u derivabilna u  akko postoje akko postoje 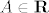 i i 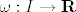 takva da takva da 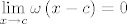 takvi da je takvi da je 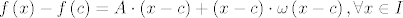 . Štoviše, tada je . Štoviše, tada je 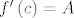 . .
E sada, uzimajući u obzir tu karakterizaciju i ono što je asistentica Hanzer rekla na vježbama: Funkcija je diferencijabilna u c pa možemo napisati 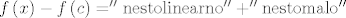 , zanima me što bi formalno bilo to "nešto malo", a za ovo nešto linearno mi se čini dosta jasno da je to diferencijal od f u c. , zanima me što bi formalno bilo to "nešto malo", a za ovo nešto linearno mi se čini dosta jasno da je to diferencijal od f u c.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 22:05 ned, 14. 1. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 17:27 sub, 20. 1. 2007 Naslov: Postano: 17:27 sub, 20. 1. 2007 Naslov: |
    |
|
|
Evo, rješenja 3. zadaće iz difrafa. Ak ne vidite odma attachment, kliknite refresh. Ak uočite grešku, javite. Pozdrav
Evo, rješenja 3. zadaće iz difrafa. Ak ne vidite odma attachment, kliknite refresh. Ak uočite grešku, javite. Pozdrav
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
| Description: |
|

Download |
| Filename: |
difrafzadaca3.doc |
| Filesize: |
400.5 KB |
| Downloaded: |
358 Time(s) |
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 16:32 sub, 27. 1. 2007 Naslov: Postano: 16:32 sub, 27. 1. 2007 Naslov: |
    |
|
|
Evo, još jedan koristan dokaz, za ograničenost linearnog operatora (Dokaz®©™ is trademark or registered trademark of Nana):
Neka je [latex]L:{\bf R}^{\bf n} \to {\bf R}^{\bf m}[/latex] linearan operator. Tada je ograničen, odnosno [latex]\left( {\exists M > 0} \right)\left( {\forall x \in {\bf R}^{\bf n} } \right)\left( {\left\| {Lx} \right\| \le M\left\| x \right\|} \right)[/latex].
Dokaz:
[latex]{\bf R}^{\bf n}[/latex] ima bazu, uzmimo kanonsku, [latex]x \in {\bf R}^{\bf n}[/latex] se može na jedinstven način prikazati kao [latex]x = \sum\limits_{i = 1}^n {\lambda _i {\bf e}_i } \Rightarrow \left\| {Ax} \right\| = \left\| {\sum\limits_{i = 1}^n {\lambda _i A{\bf e}_i } } \right\| \le \sum\limits_{i = 1}^n {\left| {\lambda _i } \right|\left\| {A{\bf e}_i } \right\|}[/latex]. Definiramo [latex]M': = \max \left\{ {\left\| {A{\bf e}_i } \right\|,i = 1...n} \right\}[/latex]. Sada imamo [latex]\left\| {Ax} \right\| \le M'\sum\limits_{i = 1}^n {\left| {\lambda _i } \right|} \le M'\sum\limits_{i = 1}^n {\left\| x \right\|_\infty } \le M'n\left\| x \right\|_\infty[/latex], a zbog ekvivalencije normi na [latex]{\bf R}^{\bf n}[/latex] slijedi da postoji [latex]M[/latex] takav da je [latex]\left\| {Ax} \right\| \le M\left\| x \right\|,\forall x \in {\bf R}^{\bf n}[/latex]
Evo, još jedan koristan dokaz, za ograničenost linearnog operatora (Dokaz®©™ is trademark or registered trademark of Nana):
Neka je 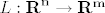 linearan operator. Tada je ograničen, odnosno linearan operator. Tada je ograničen, odnosno 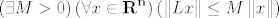 . .
Dokaz:
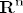 ima bazu, uzmimo kanonsku, ima bazu, uzmimo kanonsku,  se može na jedinstven način prikazati kao se može na jedinstven način prikazati kao 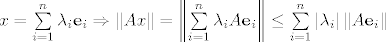 . Definiramo . Definiramo 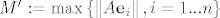 . Sada imamo . Sada imamo 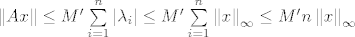 , a zbog ekvivalencije normi na , a zbog ekvivalencije normi na 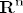 slijedi da postoji slijedi da postoji  takav da je takav da je 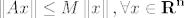
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 13:21 ned, 28. 1. 2007; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 13:30 ned, 28. 1. 2007 Naslov: Postano: 13:30 ned, 28. 1. 2007 Naslov: |
    |
|
|
Ajoj kolegice, ispričavam se, nisam znao da niste definirali normu operatora. Evo, [url]http://en.wikipedia.org/wiki/Operator_norm[/url], nadam se da će vam ovo pomoći. A ako mi ne vjerujete da je definicija dobra, dokažite da jest sami za zadaću (kak je tp znao reć, faca).
Ajoj kolegice, ispričavam se, nisam znao da niste definirali normu operatora. Evo, http://en.wikipedia.org/wiki/Operator_norm, nadam se da će vam ovo pomoći. A ako mi ne vjerujete da je definicija dobra, dokažite da jest sami za zadaću (kak je tp znao reć, faca).
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
|











