| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Tiho
Forumaš(ica)

Pridružen/a: 30. 01. 2006. (17:04:25)
Postovi: (3E)16
|
 Postano: 13:34 pon, 29. 1. 2007 Naslov: Skup {1,2,....,n} Postano: 13:34 pon, 29. 1. 2007 Naslov: Skup {1,2,....,n} |
    |
|
|
Iz skupa {1,2,....,n}na srecu odaberemo(odjednom) 3 broja.Izracunaj vjerojatnost da je
A=prvi broj po iznosu manji od drugog i treceg
B=prvi broj po iznosu izmedju drugog i treceg
Mucim se s ovim 2 dana,ako netko moze pomoci.
Hvala!
Iz skupa {1,2,....,n}na srecu odaberemo(odjednom) 3 broja.Izracunaj vjerojatnost da je
A=prvi broj po iznosu manji od drugog i treceg
B=prvi broj po iznosu izmedju drugog i treceg
Mucim se s ovim 2 dana,ako netko moze pomoci.
Hvala!
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 14:18 pon, 29. 1. 2007 Naslov: Re: Skup {1,2,....,n} Postano: 14:18 pon, 29. 1. 2007 Naslov: Re: Skup {1,2,....,n} |
    |
|
|
[quote="Tiho"]Iz skupa {1,2,....,n}na srecu odaberemo(odjednom) 3 broja.Izracunaj vjerojatnost da je
A=prvi broj po iznosu manji od drugog i treceg
B=prvi broj po iznosu izmedju drugog i treceg
Mucim se s ovim 2 dana,ako netko moze pomoci.
Hvala![/quote]
Rezultat predstavis kao uredenu trojku kojoj su sva tri elementa medusobno razlicita i iz skupa {1, ..., n}.
Tada ti je A skup uredenih trojki takvih da je prvi element najmanji (odmah je jasno da je vjerojatnost 1/3, jer je za svaki element iz trojke jednaka vjerojatnost da ce biti najmanji), pa povoljne ishode mozes prebrojati ovako:
odabir 3 elementa [latex]n \choose 3[/latex], najmanji ti je jedinstveno odreden, a preostala dva mozes permutirati na 2! = 2 nacina. Kada to podijelis sa ukupnim brojem kombinacija, [latex]{n \choose 3} \cdot 3![/latex] dobijes 1/3.
Sada je lako vidjeti da je B analogno, odmah se vidi da je za svaki element vjerojatnost da je izmedu druga dva (znaci ni najmanji ni najveci) opet 1/3, a mozes to i racunati na potpuno analogan nacin.
| Tiho (napisa): | Iz skupa {1,2,....,n}na srecu odaberemo(odjednom) 3 broja.Izracunaj vjerojatnost da je
A=prvi broj po iznosu manji od drugog i treceg
B=prvi broj po iznosu izmedju drugog i treceg
Mucim se s ovim 2 dana,ako netko moze pomoci.
Hvala! |
Rezultat predstavis kao uredenu trojku kojoj su sva tri elementa medusobno razlicita i iz skupa {1, ..., n}.
Tada ti je A skup uredenih trojki takvih da je prvi element najmanji (odmah je jasno da je vjerojatnost 1/3, jer je za svaki element iz trojke jednaka vjerojatnost da ce biti najmanji), pa povoljne ishode mozes prebrojati ovako:
odabir 3 elementa 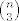 , najmanji ti je jedinstveno odreden, a preostala dva mozes permutirati na 2! = 2 nacina. Kada to podijelis sa ukupnim brojem kombinacija, , najmanji ti je jedinstveno odreden, a preostala dva mozes permutirati na 2! = 2 nacina. Kada to podijelis sa ukupnim brojem kombinacija, 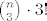 dobijes 1/3. dobijes 1/3.
Sada je lako vidjeti da je B analogno, odmah se vidi da je za svaki element vjerojatnost da je izmedu druga dva (znaci ni najmanji ni najveci) opet 1/3, a mozes to i racunati na potpuno analogan nacin.
_________________
Bri
|
|
| [Vrh] |
|
Tiho
Forumaš(ica)

Pridružen/a: 30. 01. 2006. (17:04:25)
Postovi: (3E)16
|
 Postano: 16:15 pon, 29. 1. 2007 Naslov: Re: Skup {1,2,....,n} Postano: 16:15 pon, 29. 1. 2007 Naslov: Re: Skup {1,2,....,n} |
    |
|
|
[quote="Grga"][quote="Tiho"]Iz skupa {1,2,....,n}na srecu odaberemo(odjednom) 3 broja.Izracunaj vjerojatnost da je
A=prvi broj po iznosu manji od drugog i treceg
B=prvi broj po iznosu izmedju drugog i treceg
Mucim se s ovim 2 dana,ako netko moze pomoci.
Hvala![/quote]
Rezultat predstavis kao uredenu trojku kojoj su sva tri elementa medusobno razlicita i iz skupa {1, ..., n}.
Tada ti je A skup uredenih trojki takvih da je prvi element najmanji (odmah je jasno da je vjerojatnost 1/3, jer je za svaki element iz trojke jednaka vjerojatnost da ce biti najmanji), pa povoljne ishode mozes prebrojati ovako:
odabir 3 elementa [latex]n \choose 3[/latex], najmanji ti je jedinstveno odreden, a preostala dva mozes permutirati na 2! = 2 nacina. Kada to podijelis sa ukupnim brojem kombinacija, [latex]{n \choose 3} \cdot 3![/latex] dobijes 1/3.
Sada je lako vidjeti da je B analogno, odmah se vidi da je za svaki element vjerojatnost da je izmedu druga dva (znaci ni najmanji ni najveci) opet 1/3, a mozes to i racunati na potpuno analogan nacin.[/quote]
Hvala :D
| Grga (napisa): | | Tiho (napisa): | Iz skupa {1,2,....,n}na srecu odaberemo(odjednom) 3 broja.Izracunaj vjerojatnost da je
A=prvi broj po iznosu manji od drugog i treceg
B=prvi broj po iznosu izmedju drugog i treceg
Mucim se s ovim 2 dana,ako netko moze pomoci.
Hvala! |
Rezultat predstavis kao uredenu trojku kojoj su sva tri elementa medusobno razlicita i iz skupa {1, ..., n}.
Tada ti je A skup uredenih trojki takvih da je prvi element najmanji (odmah je jasno da je vjerojatnost 1/3, jer je za svaki element iz trojke jednaka vjerojatnost da ce biti najmanji), pa povoljne ishode mozes prebrojati ovako:
odabir 3 elementa 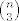 , najmanji ti je jedinstveno odreden, a preostala dva mozes permutirati na 2! = 2 nacina. Kada to podijelis sa ukupnim brojem kombinacija, , najmanji ti je jedinstveno odreden, a preostala dva mozes permutirati na 2! = 2 nacina. Kada to podijelis sa ukupnim brojem kombinacija, 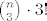 dobijes 1/3. dobijes 1/3.
Sada je lako vidjeti da je B analogno, odmah se vidi da je za svaki element vjerojatnost da je izmedu druga dva (znaci ni najmanji ni najveci) opet 1/3, a mozes to i racunati na potpuno analogan nacin. |
Hvala 
|
|
| [Vrh] |
|
Tiho
Forumaš(ica)

Pridružen/a: 30. 01. 2006. (17:04:25)
Postovi: (3E)16
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
|






