| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
FFF
Forumaš(ica)


Pridružen/a: 19. 11. 2006. (19:46:12)
Postovi: (2A)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 23:34 sub, 3. 2. 2007 Naslov: Postano: 23:34 sub, 3. 2. 2007 Naslov: |
    |
|
|
n=1 P(X^2=4)+P(X^2=9)+P(X^2=16)+...+
n=2 P(X^2=4)+P(X^2=9)+P(X^2=16)+...+
n=3 P(X^2=4)+P(X^2=9)+P(X^2=16)+...+
n=4 +P(X^2=9)+P(X^2=16)+...+
n=5 +P(X^2=9)+P(X^2=16)+...+
n=6 +P(X^2=9)+P(X^2=16)+...+
n=7 +P(X^2=9)+P(X^2=16)+...+
n=8 +P(X^2=9)+P(X^2=16)+...+
n=9 +P(X^2=16)+...+
Aha, tekst. Znači, 6. zadatak
[latex]\begin{array}{l}
\sum\limits_{n = 1}^{ + \infty } {P\left( {X^2 > n} \right)} = \sum\limits_{n = 1}^{ + \infty } {\sum\limits_{k = n + 1}^{ + \infty } {P\left( {X^2 = k} \right)} } = \sum\limits_{n = 2}^\infty {\left( {n^2 - 1} \right) \cdot P\left( {X = n} \right)} = \\
= \sum\limits_{n = 2}^\infty {\left( {n^2 - 1} \right) \cdot q^{n - 1} p} = p\sum\limits_{n = 1}^\infty {n\left( {n + 2} \right)q^n } = \\
\end{array}[/latex]
[latex]\begin{array}{l}
p \cdot \frac{{q\left( {3 - q} \right)}}{{p^3 }} = \frac{{\left( {1 - p} \right)\left( {2 + p} \right)}}{{p^2 }} = 1 \Rightarrow \\
\Rightarrow 3 - p - p^2 = p^2 \Rightarrow 2p^2 + p - 3 = 0 \Rightarrow \\
\Rightarrow p = \frac{{ - 1 + \sqrt {1 + 24} }}{4} = 1 \\
\end{array}[/latex]
I sad si mislim, ak je X geometrijska s parametrom 1, onda je [latex]\sum\limits_{n = 1}^{ + \infty } {P\left( {X^2 > n} \right)}=0[/latex], a ne 1.
n=1 P(X^2=4)+P(X^2=9)+P(X^2=16)+...+
n=2 P(X^2=4)+P(X^2=9)+P(X^2=16)+...+
n=3 P(X^2=4)+P(X^2=9)+P(X^2=16)+...+
n=4 +P(X^2=9)+P(X^2=16)+...+
n=5 +P(X^2=9)+P(X^2=16)+...+
n=6 +P(X^2=9)+P(X^2=16)+...+
n=7 +P(X^2=9)+P(X^2=16)+...+
n=8 +P(X^2=9)+P(X^2=16)+...+
n=9 +P(X^2=16)+...+
Aha, tekst. Znači, 6. zadatak
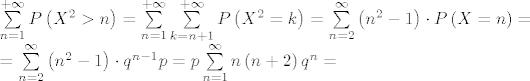
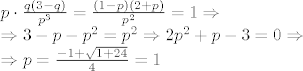
I sad si mislim, ak je X geometrijska s parametrom 1, onda je 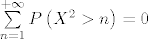 , a ne 1. , a ne 1.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 11:29 ned, 4. 2. 2007; ukupno mijenjano 4 put/a.
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
vedraf
Forumaš(ica)

Pridružen/a: 18. 09. 2006. (15:47:50)
Postovi: (BB)16
|
 Postano: 9:00 ned, 4. 2. 2007 Naslov: Postano: 9:00 ned, 4. 2. 2007 Naslov: |
    |
|
|
1.) 900
2.) a=2, b=3
3.) E[Y]=8.666, E[Z]=1.833
4.) c=4, E[X]=1
5.)E[X]=0.5, Var(X)=0.4318
8.)c=a^3/2, P(0<X<1/a)=0.0803
1.) 900
2.) a=2, b=3
3.) E[Y]=8.666, E[Z]=1.833
4.) c=4, E[X]=1
5.)E[X]=0.5, Var(X)=0.4318
8.)c=a^3/2, P(0<X<1/a)=0.0803
|
|
| [Vrh] |
|
me_me
Forumaš(ica)

Pridružen/a: 10. 09. 2006. (11:56:01)
Postovi: (CC)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
marijap
Forumaš(ica)


Pridružen/a: 21. 06. 2006. (19:04:40)
Postovi: (209)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
ivo34
Forumaš(ica)


Pridružen/a: 03. 02. 2005. (10:11:04)
Postovi: (171)16
Spol: 
|
 Postano: 16:00 ned, 4. 2. 2007 Naslov: Postano: 16:00 ned, 4. 2. 2007 Naslov: |
    |
|
|
Ovako, u vezi 4. zadace, nije mi jasna jedna stvar. :?
Dobijem slucajne varijable za funkcije distribucije (u 4. zadatku): prva je >4, a druga 1.844661968. Da li treba gledati u tablici za ovu drugu pod 1.84 ili pod 1.85. Ja sam bio uzeo 1.84 i dobio rezultat na kraju zadatka 0.0329. A alen je dobio 0.0322, znaci on je gledao za 1.85 u tablici.
Znaci, kako treba zaokruziti 1.844: na 1.84 ili 1.85 :?:
Btw, vidio sam da su neki ljudi stavili jos neka rjesenja tog zadatka, koje je na kraju tocno?
Ovako, u vezi 4. zadace, nije mi jasna jedna stvar. 
Dobijem slucajne varijable za funkcije distribucije (u 4. zadatku): prva je >4, a druga 1.844661968. Da li treba gledati u tablici za ovu drugu pod 1.84 ili pod 1.85. Ja sam bio uzeo 1.84 i dobio rezultat na kraju zadatka 0.0329. A alen je dobio 0.0322, znaci on je gledao za 1.85 u tablici.
Znaci, kako treba zaokruziti 1.844: na 1.84 ili 1.85 
Btw, vidio sam da su neki ljudi stavili jos neka rjesenja tog zadatka, koje je na kraju tocno?
|
|
| [Vrh] |
|
me_me
Forumaš(ica)

Pridružen/a: 10. 09. 2006. (11:56:01)
Postovi: (CC)16
|
 Postano: 17:38 ned, 4. 2. 2007 Naslov: Postano: 17:38 ned, 4. 2. 2007 Naslov: |
    |
|
|
[quote="ivo34"]
Znaci, kako treba zaokruziti 1.844: na 1.84 ili 1.85 :?:
Btw, vidio sam da su neki ljudi stavili jos neka rjesenja tog zadatka, koje je na kraju tocno?[/quote]
Na vjezbama smo radili bez nekog posebnog zaokruzivanja, dakle 1.84.
Tocno rj je 0.0329. No, i da uzmes 1.85 mislim da ti asistenti nece uzeti za gresku jer je razlika minimalna.
| ivo34 (napisa): |
Znaci, kako treba zaokruziti 1.844: na 1.84 ili 1.85 
Btw, vidio sam da su neki ljudi stavili jos neka rjesenja tog zadatka, koje je na kraju tocno? |
Na vjezbama smo radili bez nekog posebnog zaokruzivanja, dakle 1.84.
Tocno rj je 0.0329. No, i da uzmes 1.85 mislim da ti asistenti nece uzeti za gresku jer je razlika minimalna.
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 18:05 ned, 4. 2. 2007 Naslov: Postano: 18:05 ned, 4. 2. 2007 Naslov: |
    |
|
|
[quote="nana"][quote="alen"]
[latex]\begin{array}{l}
\sum\limits_{n = 1}^{ + \infty } {P\left( {X^2 > n} \right)} = \sum\limits_{n = 1}^{ + \infty } {\sum\limits_{k = n + 1}^{ + \infty } {P\left( {X^2 = k} \right)} } = \sum\limits_{n = 2}^\infty {\left( {n^2 - 1} \right) \cdot P\left( {X = n} \right)} = \\
= \sum\limits_{n = 2}^\infty {\left( {n^2 - 1} \right) \cdot q^{n - 1} p} = p\sum\limits_{n = 1}^\infty {n\left( {n + 2} \right)q^n } = \\
\end{array}[/latex]
[latex]\begin{array}{l}
p \cdot \frac{{q\left( {3 - q} \right)}}{{p^3 }} = \frac{{\left( {1 - p} \right)\left( {2 + p} \right)}}{{p^2 }} = 1 \Rightarrow \\
\Rightarrow 3 - p - p^2 = p^2 \Rightarrow 2p^2 + p - 3 = 0 \Rightarrow \\
\Rightarrow p = \frac{{ - 1 + \sqrt {1 + 24} }}{4} = 1 \\
\end{array}[/latex]
[/quote]Krivo si izracunao kvadratnu jednadzbu, treba biti [color=red]2[/color] - p - p^2 = p^2 :D
al opet dobijes korijen iz 17 htio ne htio 8)[/quote]
e, tako je, hvala
1. [latex]n \ge 900[/latex]
2. [latex]\left( {a,b} \right) = \left( {2,3} \right)[/latex]
3. [latex]EY = \frac{{26}}{3}[/latex]
[latex]EZ = \frac{{11}}{6}[/latex]
4. [latex]c = 4[/latex], [latex]EX = 2[/latex]
5.
[latex]P\left( {X = k} \right) = \frac{{\left( \begin{array}{c}
10 \\
k \\
\end{array} \right)\left( \begin{array}{c}
100 - 10 \\
5 - k \\
\end{array} \right)}}{{\left( \begin{array}{c}
100 \\
5 \\
\end{array} \right)}}[/latex], [latex]EX = \frac{1}{2}[/latex], [latex]Var\left( X \right) = \frac{{19}}{{44}}[/latex]
6. [latex]\frac{{\sqrt {17} - 1}}{4}[/latex]
8. [latex]c = \frac{{a^3 }}{2},P\left( {X \in \left\langle {0,\frac{1}{a}} \right\rangle } \right) = \frac{{2 - 5e^{ - 1} }}{2}[/latex]
9. [latex]P\left( {1 \le X \le 3} \right) = \frac{1}{4},P\left( {X > 3\left| {X > 1} \right.} \right) = \frac{1}{2}[/latex]
| nana (napisa): | | alen (napisa): |
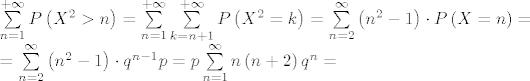
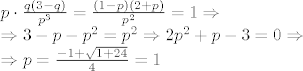
|
Krivo si izracunao kvadratnu jednadzbu, treba biti 2 - p - p^2 = p^2 
al opet dobijes korijen iz 17 htio ne htio  |
e, tako je, hvala
1. 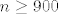
2. 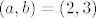
3. 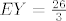
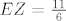
4.  , , 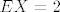
5.
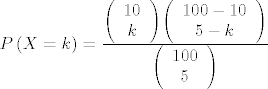 , , 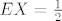 , , 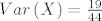
6. 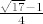
8. 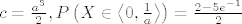
9. 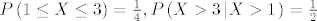
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
aenima
Forumaš(ica)

Pridružen/a: 17. 09. 2004. (17:03:42)
Postovi: (57)16
Spol: 
|
 Postano: 21:14 ned, 4. 2. 2007 Naslov: Postano: 21:14 ned, 4. 2. 2007 Naslov: |
    |
|
|
1. n=900
2. a=2, b=3
3. EY=8.6. , EZ=1.83.
4. c=4, EX=2
5. EX=0.5, VarX=0.431818.
6. p=(sqrt(17)-1)/4
8.c=0.5a^3, P(X iz <0,1/a>)=0.0803
9. 0.25, 0.5
Mislim da n mora bit točno 900 ni više ni manje jer je vjerojatnost zadana jednakošću a ne nejednakošću.
1. n=900
2. a=2, b=3
3. EY=8.6. , EZ=1.83.
4. c=4, EX=2
5. EX=0.5, VarX=0.431818.
6. p=(sqrt(17)-1)/4
8.c=0.5a^3, P(X iz <0,1/a>)=0.0803
9. 0.25, 0.5
Mislim da n mora bit točno 900 ni više ni manje jer je vjerojatnost zadana jednakošću a ne nejednakošću.
|
|
| [Vrh] |
|
Greda
Forumaš(ica)
Pridružen/a: 01. 07. 2006. (14:00:26)
Postovi: (44)16
Spol: 
|
|
| [Vrh] |
|
marijap
Forumaš(ica)


Pridružen/a: 21. 06. 2006. (19:04:40)
Postovi: (209)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
aenima
Forumaš(ica)

Pridružen/a: 17. 09. 2004. (17:03:42)
Postovi: (57)16
Spol: 
|
|
| [Vrh] |
|
|













