| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Mojo
Forumaš(ica)


Pridružen/a: 28. 02. 2006. (12:37:23)
Postovi: (3F)16
|
 Postano: 16:33 pon, 18. 9. 2006 Naslov: Postano: 16:33 pon, 18. 9. 2006 Naslov: |
    |
|
|
e je si me ubola.. na to san pa bija. dakle, e=lim(1+1/k)^k, ali mi smo ga bas tako definirali, tj. neznamo njegovu tocnu vrijednost, pa nemozes rec da je lim(1+1/k)^k=lim(1+1/k)^k, jer nema smisla. Znaci moras rec da kako je to monoton i ogranicen niz u |R, da je onda konvergenrtan, al mi zapravo nemozemo tocno odredit broj, jer je iracionalan, pa smo ga nazvali e. I onda jos potpitanje, da li je cauchyev u |R, je, da li je cauchyev u Q, je zato jer je Q podskup od |R, a metrika ostaje ista, da li je konvergentan u Q, nije jer je e iz R/Q. Eto.
e je si me ubola.. na to san pa bija. dakle, e=lim(1+1/k)^k, ali mi smo ga bas tako definirali, tj. neznamo njegovu tocnu vrijednost, pa nemozes rec da je lim(1+1/k)^k=lim(1+1/k)^k, jer nema smisla. Znaci moras rec da kako je to monoton i ogranicen niz u |R, da je onda konvergenrtan, al mi zapravo nemozemo tocno odredit broj, jer je iracionalan, pa smo ga nazvali e. I onda jos potpitanje, da li je cauchyev u |R, je, da li je cauchyev u Q, je zato jer je Q podskup od |R, a metrika ostaje ista, da li je konvergentan u Q, nije jer je e iz R/Q. Eto.
|
|
| [Vrh] |
|
spuzvica
Forumaš(ica)

Pridružen/a: 20. 01. 2006. (19:55:43)
Postovi: (39)16
|
|
| [Vrh] |
|
Mojo
Forumaš(ica)


Pridružen/a: 28. 02. 2006. (12:37:23)
Postovi: (3F)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 18:56 pon, 18. 9. 2006 Naslov: Postano: 18:56 pon, 18. 9. 2006 Naslov: |
    |
|
|
[quote="spuzvica"]I evo mene opet :frustriran:
Kako da dokazem da niz (1+1/k)^k konvergira prema e ?
Aj pomozite :blinking:[/quote]
Iz knjige Matematička Analiza (U n-dimenizionalnom realnom prostoru, prvi dio), Sibe Mardešić (str. 117).
Neka je [latex]\xi_n=\left ( 1+ \frac{1}{n} \right )^n[/latex]
Pokazat ćemo da niz (zadani) strogo raste i da je omeđen odozgo.
Po binomnoj formuli [latex](x+y)^n=\sum_{i=0}^n {n \choose i}x^i y^{n-i} [/latex] vrijedi:
[latex]\left ( 1+ \frac{1}{n} \right )^n=\sum_{k=0}^n {n \choose k}1^{n-k} \frac{1}{n^k}[/latex]
što nakon sređivanja daje:
[latex]\left ( 1+ \frac{1}{n} \right )^n=\sum_{k=0}^n \frac{1}{k!}1 \cdot \left ( 1- \frac{1}{n} \right )\left ( 1- \frac{2}{n} \right )\dots \left ( 1- \frac{k-1}{n} \right )[/latex]
Očito je da je
[latex]\left ( 1+ \frac{1}{n} \right )^n \leq \sum_{k=0}^n \frac{1}{k!}[/latex]
a indukcijom se lako pokaže da je [latex]k! \geq 2^{k-1}[/latex] za svaki k prirodni broj i zato je:
[latex]\sum_{k=0}^n \frac{1}{k!} \leq 1+ \sum_{k=1}^n \frac{1}{2^{k-1}}[/latex]
Iz prethodne dvije nejednakosti i formule:
[latex](1-\xi)\sum_{k=1}^n \xi^{k-1}=1-\xi^n, \quad \xi \in \mathbb{R}[/latex]
za [latex]\xi=\frac{1}{2}[/latex] dobiva se
[latex]\xi_n=\left ( 1+ \frac{1}{n} \right )^n \leq 1+2 \left(1-\frac{1}{2^n} \right ) \leq 3[/latex]
Zaključili smo da je niz [latex](\xi_n)[/latex] omeđen odozgo, još trebamo provjeriti da je rastući, tj. treba se provjeriti:
[latex]\left ( 1+ \frac{1}{n} \right )^n < \left ( 1+ \frac{1}{n+1} \right )^{n+1}[/latex]
To očito vrijedi (iz onog raspisa negdje iznad se pokaže).
Kako je [latex]\xi_1=2[/latex] očito je
[latex]2 < e \leq 3[/latex]
| spuzvica (napisa): | I evo mene opet 
Kako da dokazem da niz (1+1/k)^k konvergira prema e ?
Aj pomozite  |
Iz knjige Matematička Analiza (U n-dimenizionalnom realnom prostoru, prvi dio), Sibe Mardešić (str. 117).
Neka je 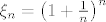
Pokazat ćemo da niz (zadani) strogo raste i da je omeđen odozgo.
Po binomnoj formuli 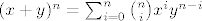 vrijedi: vrijedi:
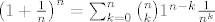
što nakon sređivanja daje:
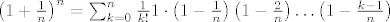
Očito je da je
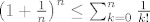
a indukcijom se lako pokaže da je 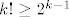 za svaki k prirodni broj i zato je: za svaki k prirodni broj i zato je:
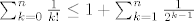
Iz prethodne dvije nejednakosti i formule:
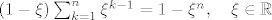
za  dobiva se dobiva se
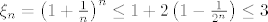
Zaključili smo da je niz 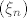 omeđen odozgo, još trebamo provjeriti da je rastući, tj. treba se provjeriti: omeđen odozgo, još trebamo provjeriti da je rastući, tj. treba se provjeriti:
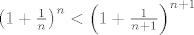
To očito vrijedi (iz onog raspisa negdje iznad se pokaže).
Kako je 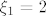 očito je očito je
_________________
The Dude Abides
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
spuzvica
Forumaš(ica)

Pridružen/a: 20. 01. 2006. (19:55:43)
Postovi: (39)16
|
|
| [Vrh] |
|
spuzvica
Forumaš(ica)

Pridružen/a: 20. 01. 2006. (19:55:43)
Postovi: (39)16
|
 Postano: 0:49 pet, 22. 9. 2006 Naslov: Postano: 0:49 pet, 22. 9. 2006 Naslov: |
    |
|
|
Opet problemi :?
U trecem poglavlju, kod dokaza leme 16.3. da je graf neprekidne realne f-je fi:[a,b]-->R skup povrsine nula, tribamo dokazat da za svaki epsilon>0 postoji konacni pokrivac {I1,...In} skupa graf f-je fi pravokutnicima Ij takav da je suma povrsina tih pravokutnika < epsilon....(bar ja mislin)
E sad se to dokazuje i dokazuje i sve mi je jasno (a mozda i nije :wink: ) do zadnje crte kad se dobije da je suma povrsina pravokutnika = epsilon. Pa zar nismo tribali dokazat da je < od epsilon, a ne jednako?? :?
Opet problemi 
U trecem poglavlju, kod dokaza leme 16.3. da je graf neprekidne realne f-je fi:[a,b]→R skup povrsine nula, tribamo dokazat da za svaki epsilon>0 postoji konacni pokrivac {I1,...In} skupa graf f-je fi pravokutnicima Ij takav da je suma povrsina tih pravokutnika < epsilon....(bar ja mislin)
E sad se to dokazuje i dokazuje i sve mi je jasno (a mozda i nije  ) do zadnje crte kad se dobije da je suma povrsina pravokutnika = epsilon. Pa zar nismo tribali dokazat da je < od epsilon, a ne jednako?? ) do zadnje crte kad se dobije da je suma povrsina pravokutnika = epsilon. Pa zar nismo tribali dokazat da je < od epsilon, a ne jednako?? 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 2:46 pet, 22. 9. 2006 Naslov: Postano: 2:46 pet, 22. 9. 2006 Naslov: |
    |
|
|
Puno puta je receno: [b]svejedno je[/b], jer mora vrijediti za svaki epsilon. 8) Ako ti dokazes [latex]\leq[/latex], onda mozes uzeti [latex]\frac\epsilon{2}[/latex], pa ce i za njega vrijediti [latex]\leq\frac\epsilon{2}[/latex], tj. [latex]<\epsilon[/latex]. ;)
Ovo je [b]vazno razumjeti[/b], pa se zamisli nad tim dok nisi sigurna da ti je jasno (tj. nemoj uzeti zdravo za gotovo). ;)
Puno puta je receno: svejedno je, jer mora vrijediti za svaki epsilon.  Ako ti dokazes Ako ti dokazes 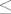 , onda mozes uzeti , onda mozes uzeti 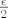 , pa ce i za njega vrijediti , pa ce i za njega vrijediti 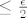 , tj. , tj. 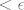 . . 
Ovo je vazno razumjeti, pa se zamisli nad tim dok nisi sigurna da ti je jasno (tj. nemoj uzeti zdravo za gotovo). 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
gzr
Forumaš(ica)

Pridružen/a: 06. 02. 2007. (12:38:35)
Postovi: (4)16
|
 Postano: 12:57 uto, 6. 2. 2007 Naslov: Postano: 12:57 uto, 6. 2. 2007 Naslov: |
    |
|
|
Ucim Ma3 za usmeni pa imam par pitanja i nejasnoca, ako netko zna bio bih jako zahvalan da sto prije odgovori:
1. Kako aksiom o postojanju supremuma u svakom podskupu od R pravi razliku skupova realnih brojeva R i skupa rac. brojeva Q? (ako uopce jest tako...) Ako to nije razlika R i Q, koja je [u]aksiomatska[/u] razlika?
2. ako S podskup metrickog prostora X, je li pravilno govoriti o S kao metrickom prostoru ili treba reci da je to metricki potprostor sa restrikcijom metrike od X na S ili je svejedno kako rekli?
3. Ako kazemo da je Pk niz [b]iz[/b] metrickog prostora X i Pk niz [b]u[/b] m.p. X, koja je razlika u tome sto smo rekli?
4. na ovim pitanjima s usmenih koji su na forumu nisam nigdje primijetio one teoreme nakon Banachovog tm o fixnoj tocki ( to su oni gdje dokazujemo svojstva i sto vec o prostoru nep. omeđenih funkcija BC(X, Y) ). Da li netko zna da li je profesor pitao kada nesto o tom na usmenom ili dokaze tih teorema?
hvala... :-)
Ucim Ma3 za usmeni pa imam par pitanja i nejasnoca, ako netko zna bio bih jako zahvalan da sto prije odgovori:
1. Kako aksiom o postojanju supremuma u svakom podskupu od R pravi razliku skupova realnih brojeva R i skupa rac. brojeva Q? (ako uopce jest tako...) Ako to nije razlika R i Q, koja je aksiomatska razlika?
2. ako S podskup metrickog prostora X, je li pravilno govoriti o S kao metrickom prostoru ili treba reci da je to metricki potprostor sa restrikcijom metrike od X na S ili je svejedno kako rekli?
3. Ako kazemo da je Pk niz iz metrickog prostora X i Pk niz u m.p. X, koja je razlika u tome sto smo rekli?
4. na ovim pitanjima s usmenih koji su na forumu nisam nigdje primijetio one teoreme nakon Banachovog tm o fixnoj tocki ( to su oni gdje dokazujemo svojstva i sto vec o prostoru nep. omeđenih funkcija BC(X, Y) ). Da li netko zna da li je profesor pitao kada nesto o tom na usmenom ili dokaze tih teorema?
hvala... 
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 10:50 sri, 7. 2. 2007 Naslov: Postano: 10:50 sri, 7. 2. 2007 Naslov: |
    |
|
|
Za ovo prvo, uzmi skup
[latex]S = \{x : x < \sqrt{2}\}[/latex]
Taj skup ima supremum u skupu realnih brojeva, [latex]\sqrt{2} \notin Q[/latex], no kak oto nije racionalan broj, nema supremum u skupu racionalnih brojeva (ne mozes odrediti prvi manji racionalan broj).
Za trece pitanje, buduci da je niz funkcija iz skupa prirodnih brojeva u neki drugi skup, ako kazemo da je niz iz metrickog prostora X, to bi se moglo protumaciti kao da kazemo da je funkcija kojoj je domena m.p. X - to je barem moje videnje situacije.
Za ovo prvo, uzmi skup
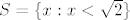
Taj skup ima supremum u skupu realnih brojeva, 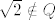 , no kak oto nije racionalan broj, nema supremum u skupu racionalnih brojeva (ne mozes odrediti prvi manji racionalan broj). , no kak oto nije racionalan broj, nema supremum u skupu racionalnih brojeva (ne mozes odrediti prvi manji racionalan broj).
Za trece pitanje, buduci da je niz funkcija iz skupa prirodnih brojeva u neki drugi skup, ako kazemo da je niz iz metrickog prostora X, to bi se moglo protumaciti kao da kazemo da je funkcija kojoj je domena m.p. X - to je barem moje videnje situacije.
_________________
Bri
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 18:41 sri, 7. 2. 2007 Naslov: Postano: 18:41 sri, 7. 2. 2007 Naslov: |
    |
|
|
[quote="Grga"] :roll:[/quote]
malo si razdrazljiv? :wicked:
ispricavam se sto to nije u svim knjigama.
[b]edit[/b]: ocito Grx brze mijenja svoj post nego sto ja postam. Za utjehu, prepisat cu vam cijelu jednu recenicu iz [u]moje[/u] knjige.
"U vezi s označivanjem funkcija (preslikavanja) i [i]čitanja[/i] označenog, napomenimo i sljedeće: f: X -> Y se čita "preslikavanje (funkcija) f s X [i]u[/i] Y", a ne "[i]na[/i] Y". Kad se kaže [i]na[/i], to znači da je f surjekcija, pa ako nemamo [i]zaista[/i] posla sa surjektivnim preslikavanjem, treba kazati [i]u[/i].
| Grga (napisa): |  |
malo si razdrazljiv? 
ispricavam se sto to nije u svim knjigama.
edit: ocito Grx brze mijenja svoj post nego sto ja postam. Za utjehu, prepisat cu vam cijelu jednu recenicu iz moje knjige.
"U vezi s označivanjem funkcija (preslikavanja) i čitanja označenog, napomenimo i sljedeće: f: X → Y se čita "preslikavanje (funkcija) f s X u Y", a ne "na Y". Kad se kaže na, to znači da je f surjekcija, pa ako nemamo zaista posla sa surjektivnim preslikavanjem, treba kazati u.
|
|
| [Vrh] |
|
Ada
Forumaš(ica)

Pridružen/a: 19. 09. 2006. (16:49:15)
Postovi: (1B)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 14:37 pon, 27. 8. 2007 Naslov: Postano: 14:37 pon, 27. 8. 2007 Naslov: |
    |
|
|
[quote="Ada"]Alo,ljudi!
Evo ja tek krenuh s ucenjem i nisu mi bas jasne neke stvari.
evo koje:
Kaze u knjizi prof Ungar da je u metrickom prostoru 1-clani skup zatvoren,a u topoloskom nije.Zasto to?[/quote]
Takvi prostori se zovu T1 prostori, i nisu svi topoloski prostori T1 prostori.
[quote="Ada"]
I kaze da u metrickom prostoru svake 2 razlicite tocke imaju medusobno disjunktne okoline,a u topoloskom ne.
Ne kuzim zasto,pa molim nekog da mi to pokusa razjasniti. :?:[/quote]
Ovi prostori se zovu Hausdorffovi prostori, i takoder nisu svi topoloski ujedno i Hausdorffovi, a sad na tvoje pitanje: cim imas metriku odmah dobijes i topoloski prostor, mozes def. otvorenu kuglu, i dobijes topoloski prostor induciran metrikom, i tu nacelno je sve jasno. No postoje topologije koje nisu inducirane metrikom i tu moze doci do 'problema', jer naprosto ne mozes govoriti o otvorenim kuglama.
Primjere takvih topologija cu ti kasnije napisati, no puno teze je dokazati da takve topologije nisu induciranje normom, nego smisliti same primjere.
Da se jos vratim na tvoje pitanje, zasto nema problema u metrickim prostorima, no ako imas dvije razlicite tocke uzmes njihovu udaljenost i dvije kugle koje imaju za srediste te tocke radijusa polovice njihove udaljenosti i imas disjunktne okoline, no moze primjetiti da sam govorio o udaljenosti, sto zapravo znaci da imas normu, ili metriku na tom skupu.Onda mozes govoriti o jedinstvenosti limesa,unifornmom neprekidnoscu i slicnim cudima.
Slicno za zatvorene skupove.
Probaj na wikipediji, pogledati nesta o topoloskim prostorima,Haussdorffovim prostorima, T0,T1,T2,... prostorima. Nadam se da ce onda biti jasnije.
Btw. ja jos nisam slusao topologiju, pa se nadam da ce se javiti netko sa teorijske da jos bolje objasni.
| Ada (napisa): | Alo,ljudi!
Evo ja tek krenuh s ucenjem i nisu mi bas jasne neke stvari.
evo koje:
Kaze u knjizi prof Ungar da je u metrickom prostoru 1-clani skup zatvoren,a u topoloskom nije.Zasto to? |
Takvi prostori se zovu T1 prostori, i nisu svi topoloski prostori T1 prostori.
| Ada (napisa): |
I kaze da u metrickom prostoru svake 2 razlicite tocke imaju medusobno disjunktne okoline,a u topoloskom ne.
Ne kuzim zasto,pa molim nekog da mi to pokusa razjasniti.  |
Ovi prostori se zovu Hausdorffovi prostori, i takoder nisu svi topoloski ujedno i Hausdorffovi, a sad na tvoje pitanje: cim imas metriku odmah dobijes i topoloski prostor, mozes def. otvorenu kuglu, i dobijes topoloski prostor induciran metrikom, i tu nacelno je sve jasno. No postoje topologije koje nisu inducirane metrikom i tu moze doci do 'problema', jer naprosto ne mozes govoriti o otvorenim kuglama.
Primjere takvih topologija cu ti kasnije napisati, no puno teze je dokazati da takve topologije nisu induciranje normom, nego smisliti same primjere.
Da se jos vratim na tvoje pitanje, zasto nema problema u metrickim prostorima, no ako imas dvije razlicite tocke uzmes njihovu udaljenost i dvije kugle koje imaju za srediste te tocke radijusa polovice njihove udaljenosti i imas disjunktne okoline, no moze primjetiti da sam govorio o udaljenosti, sto zapravo znaci da imas normu, ili metriku na tom skupu.Onda mozes govoriti o jedinstvenosti limesa,unifornmom neprekidnoscu i slicnim cudima.
Slicno za zatvorene skupove.
Probaj na wikipediji, pogledati nesta o topoloskim prostorima,Haussdorffovim prostorima, T0,T1,T2,... prostorima. Nadam se da ce onda biti jasnije.
Btw. ja jos nisam slusao topologiju, pa se nadam da ce se javiti netko sa teorijske da jos bolje objasni.
|
|
| [Vrh] |
|
Ada
Forumaš(ica)

Pridružen/a: 19. 09. 2006. (16:49:15)
Postovi: (1B)16
|
|
| [Vrh] |
|
Ada
Forumaš(ica)

Pridružen/a: 19. 09. 2006. (16:49:15)
Postovi: (1B)16
|
 Postano: 17:06 sub, 1. 9. 2007 Naslov: Postano: 17:06 sub, 1. 9. 2007 Naslov: |
    |
|
|
Evo jos nekih nejasnoca i nesigurnosti. :(
(1)Da li fja moze biti neprekidna u nekoj tocki,a da u toj tocki nema limes?
(Ja bih rekla metrickom prostoru ne,a u topolskom ?)
(2)U kakvoj su vezi gomiliste niza i gomiliste skupa vrijednosti niza?
Npr, niz (-1)^k ima gomilista -1 i 1,a skup vrijednosti je {-1,1}.Taj skup nema gomiliste,kaj ne?Onda te 2.stvari nemaju veze jedna s drugom?
(3)Da li B-W tm vrijedi u svakom metrickom prostoru?Da li vrijedi u konacnodim. metrickom prostoru rac.brojeva?(ne,jer skup rac br nije ogranicen,a i ogranicenost smo def samo za niz u R^n)
(4)da li je podniz ogranicenog niza ogranicen?(ne,jer je podniz f°u:N->X,a u:N->N je stogo uzlazna pa onda i neogranicena)
Ovo u zagradi su moja nagadanja.
Molim nekog da mi odgovori i da me ispravi ako grijesim!
Evo jos nekih nejasnoca i nesigurnosti. 
(1)Da li fja moze biti neprekidna u nekoj tocki,a da u toj tocki nema limes?
(Ja bih rekla metrickom prostoru ne,a u topolskom ?)
(2)U kakvoj su vezi gomiliste niza i gomiliste skupa vrijednosti niza?
Npr, niz (-1)^k ima gomilista -1 i 1,a skup vrijednosti je {-1,1}.Taj skup nema gomiliste,kaj ne?Onda te 2.stvari nemaju veze jedna s drugom?
(3)Da li B-W tm vrijedi u svakom metrickom prostoru?Da li vrijedi u konacnodim. metrickom prostoru rac.brojeva?(ne,jer skup rac br nije ogranicen,a i ogranicenost smo def samo za niz u R^n)
(4)da li je podniz ogranicenog niza ogranicen?(ne,jer je podniz f°u:N->X,a u:N->N je stogo uzlazna pa onda i neogranicena)
Ovo u zagradi su moja nagadanja.
Molim nekog da mi odgovori i da me ispravi ako grijesim!
|
|
| [Vrh] |
|
Blatko
Forumaš(ica)

Pridružen/a: 12. 07. 2007. (11:25:44)
Postovi: (5D)16
|
 Postano: 18:16 sub, 1. 9. 2007 Naslov: Postano: 18:16 sub, 1. 9. 2007 Naslov: |
    |
|
|
[quote="Ada"]Evo jos nekih nejasnoca i nesigurnosti. :(
(1)Da li fja moze biti neprekidna u nekoj tocki,a da u toj tocki nema limes?
(Ja bih rekla metrickom prostoru ne,a u topolskom ?)
(2)U kakvoj su vezi gomiliste niza i gomiliste skupa vrijednosti niza?
Npr, niz (-1)^k ima gomilista -1 i 1,a skup vrijednosti je {-1,1}.Taj skup nema gomiliste,kaj ne?Onda te 2.stvari nemaju veze jedna s drugom?
(3)Da li B-W tm vrijedi u svakom metrickom prostoru?Da li vrijedi u konacnodim. metrickom prostoru rac.brojeva?(ne,jer skup rac br nije ogranicen,a i ogranicenost smo def samo za niz u R^n)
(4)da li je podniz ogranicenog niza ogranicen?(ne,jer je podniz f°u:N->X,a u:N->N je stogo uzlazna pa onda i neogranicena)
Ovo u zagradi su moja nagadanja.
Molim nekog da mi odgovori i da me ispravi ako grijesim![/quote]
(1) Može, ali samo ako ta točka nije gomilište skupa na kojem je ta f-ja definirana (naime, definicija limesa traži da točka u kojoj f-ja ima limes bude gomilište skupa na kojem je definirana). Npr., funkcija definirana na jednočlanom skupu je uvijek neprekidna (bez obzira koju topologiju gledamo), ali nema limes (u npr.) T1 prostorima(jer jednočlan skup u T1 prostoru nema gomilišta).
(2) Općenito, nema veze jedno s drugim.
(3) Postoji niz u Q koji ima limes u R \ Q (to se moze vidjeti ovako: za danu točku xo iz R \ Q i dani n iz N postoji xn iz Q takav da je xn iz <xo - 1/n, xo + 1/n> (gustoća od Q u R). Jasno je da niz (xn: n iz N) ima limes xo. U drugu ruku, konvergentan niz je omeđen i ima samo jedno gomilište - njegov limes (koji u ovom slučaju nije u Q).).
(4) PODNIZ OMEĐENOG NIZA JE OMEĐEN. To slijedi iz činjenice da je skup vrijednosti koje poprima podniz sadržan uskupu vrijednosti koje poprima sam niz.Inače, za funkciju f : S -> X (gdje je X nužno metrički prostor) govorimo da je omeđena ako je f(S) (dakle, slika od f) omeđen skup (tj., ako je f(S) sadržan u nekoj kugli u X).
| Ada (napisa): | Evo jos nekih nejasnoca i nesigurnosti. 
(1)Da li fja moze biti neprekidna u nekoj tocki,a da u toj tocki nema limes?
(Ja bih rekla metrickom prostoru ne,a u topolskom ?)
(2)U kakvoj su vezi gomiliste niza i gomiliste skupa vrijednosti niza?
Npr, niz (-1)^k ima gomilista -1 i 1,a skup vrijednosti je {-1,1}.Taj skup nema gomiliste,kaj ne?Onda te 2.stvari nemaju veze jedna s drugom?
(3)Da li B-W tm vrijedi u svakom metrickom prostoru?Da li vrijedi u konacnodim. metrickom prostoru rac.brojeva?(ne,jer skup rac br nije ogranicen,a i ogranicenost smo def samo za niz u R^n)
(4)da li je podniz ogranicenog niza ogranicen?(ne,jer je podniz f°u:N→X,a u:N→N je stogo uzlazna pa onda i neogranicena)
Ovo u zagradi su moja nagadanja.
Molim nekog da mi odgovori i da me ispravi ako grijesim! |
(1) Može, ali samo ako ta točka nije gomilište skupa na kojem je ta f-ja definirana (naime, definicija limesa traži da točka u kojoj f-ja ima limes bude gomilište skupa na kojem je definirana). Npr., funkcija definirana na jednočlanom skupu je uvijek neprekidna (bez obzira koju topologiju gledamo), ali nema limes (u npr.) T1 prostorima(jer jednočlan skup u T1 prostoru nema gomilišta).
(2) Općenito, nema veze jedno s drugim.
(3) Postoji niz u Q koji ima limes u R \ Q (to se moze vidjeti ovako: za danu točku xo iz R \ Q i dani n iz N postoji xn iz Q takav da je xn iz <xo - 1/n, xo + 1/n> (gustoća od Q u R). Jasno je da niz (xn: n iz N) ima limes xo. U drugu ruku, konvergentan niz je omeđen i ima samo jedno gomilište - njegov limes (koji u ovom slučaju nije u Q).).
(4) PODNIZ OMEĐENOG NIZA JE OMEĐEN. To slijedi iz činjenice da je skup vrijednosti koje poprima podniz sadržan uskupu vrijednosti koje poprima sam niz.Inače, za funkciju f : S → X (gdje je X nužno metrički prostor) govorimo da je omeđena ako je f(S) (dakle, slika od f) omeđen skup (tj., ako je f(S) sadržan u nekoj kugli u X).
|
|
| [Vrh] |
|
Ada
Forumaš(ica)

Pridružen/a: 19. 09. 2006. (16:49:15)
Postovi: (1B)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
|











