| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
KKK
Forumaš(ica)

Pridružen/a: 04. 05. 2005. (14:48:19)
Postovi: (4D)16
|
|
| [Vrh] |
|
Kobra
Forumaš(ica)

Pridružen/a: 03. 02. 2005. (10:23:52)
Postovi: (48)16
Spol: 
Lokacija: Ferenščica/Podstrana
|
|
| [Vrh] |
|
KKK
Forumaš(ica)

Pridružen/a: 04. 05. 2005. (14:48:19)
Postovi: (4D)16
|
 Postano: 11:28 pet, 16. 2. 2007 Naslov: Postano: 11:28 pet, 16. 2. 2007 Naslov: |
    |
|
|
Mislim da se dobro sjećaš. thnx
Neka ostane za buduće naraštaje:
Univerzalni (dobro poznati) kontraprimjer:
f_n(t)=
:arrow: -n*t-n, t€[-1,-1+1/n]
:arrow: -1, t€[-1+1/n,-1/n]
:arrow: n*t, t€[-1/n,1/n]
:arrow: 1, t€[1/n,1-1/n]
:arrow: -n*t+n, t€[1-1/n,1]
Mislim da se dobro sjećaš. thnx
Neka ostane za buduće naraštaje:
Univerzalni (dobro poznati) kontraprimjer:
f_n(t)=
 -n*t-n, t€[-1,-1+1/n] -n*t-n, t€[-1,-1+1/n]
 -1, t€[-1+1/n,-1/n] -1, t€[-1+1/n,-1/n]
 n*t, t€[-1/n,1/n] n*t, t€[-1/n,1/n]
 1, t€[1/n,1-1/n] 1, t€[1/n,1-1/n]
 -n*t+n, t€[1-1/n,1] -n*t+n, t€[1-1/n,1]
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 11:29 pet, 16. 2. 2007 Naslov: Postano: 11:29 pet, 16. 2. 2007 Naslov: |
    |
|
|
Najlakse je po definiciji:
- Funkcional F:X->C je neprekidan=ogranicen ako postoji konstanta M>=0 takva da za svaku f iz X vrijedi |F(f)|<=M*||f||.
- Funkcional F:X->C nije neprekidan=ogranicen ako takva konstanta M ne postoji, sto zapravo znaci (nakon normalizacije) da postoji niz (f_n)_n u prostoru X takav da je ||f_n||=1 za svaki n, ali |F(f_n)| konvergira u +beskonacno.
(1) Koristenjem Schwarz-Cauchy nejednakosti:
[latex]|\Phi(f)|=|\int_{-1}^1 f(t)\cdot 1 \,dt|\leq
(\int_{-1}^1 |f(t)|^2 \,dt)^\frac{1}{2} (\int_{-1}^1 1^2 \,dt)^\frac{1}{2} =\|f\| [/latex]
Dakle funkcional je neprekidan (pri cemu mozemo uzeti M=1).
(2) Za svaki prirodni broj n definiras funkciju g_n tako da bude
[latex]g_n(-1)=0, \ \ g_n(1-1/n)=0, \ \ g_n(1)=n[/latex]
a izmedju je linearna (graf dobijes tako da spojis tocke duzinama).
Sada uzmi f_n tako da bude [latex]f_n(t)=\sqrt{g_n(t)}[/latex] za svaki t iz [-1,1].
||f_n||=1, ali [latex]f_n(1)=\sqrt{n}\rightarrow +\infty[/latex]
Dakle funkcional nije neprekidan.
(3) Opet koristenjem Schwarz-Cauchy nejednakosti imamo:
[latex]|\Phi(f)|=|\int_{-1}^1 f(t)\cdot \frac{1}{\sqrt[3]{1-t^2}} \,dt|\leq
(\int_{-1}^1 |f(t)|^2 \,dt)^\frac{1}{2} (\int_{-1}^1 \frac{dt}{(1-t^2)^{2/3}})^\frac{1}{2}[/latex]
Posljednji integral je nepravi sa singularitetima u tockama t=-1 i t=1 i kao na Analizi 2 se pokazuje da konvergira. Dakle funkcional je neprekidan, pri cemu mozemo uzeti
[latex]M=(\int_{-1}^1 \frac{dt}{(1-t^2)^{2/3}})^\frac{1}{2}[/latex]
Najlakse je po definiciji:
- Funkcional F:X→C je neprekidan=ogranicen ako postoji konstanta M>=0 takva da za svaku f iz X vrijedi |F(f)|⇐M*||f||.
- Funkcional F:X→C nije neprekidan=ogranicen ako takva konstanta M ne postoji, sto zapravo znaci (nakon normalizacije) da postoji niz (f_n)_n u prostoru X takav da je ||f_n||=1 za svaki n, ali |F(f_n)| konvergira u +beskonacno.
(1) Koristenjem Schwarz-Cauchy nejednakosti:
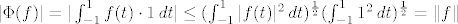
Dakle funkcional je neprekidan (pri cemu mozemo uzeti M=1).
(2) Za svaki prirodni broj n definiras funkciju g_n tako da bude
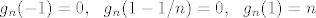
a izmedju je linearna (graf dobijes tako da spojis tocke duzinama).
Sada uzmi f_n tako da bude 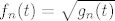 za svaki t iz [-1,1]. za svaki t iz [-1,1].
||f_n||=1, ali 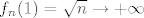
Dakle funkcional nije neprekidan.
(3) Opet koristenjem Schwarz-Cauchy nejednakosti imamo:
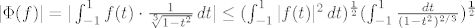
Posljednji integral je nepravi sa singularitetima u tockama t=-1 i t=1 i kao na Analizi 2 se pokazuje da konvergira. Dakle funkcional je neprekidan, pri cemu mozemo uzeti
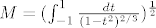
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
|







