| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Adelaide
Forumaš(ica)

Pridružen/a: 21. 02. 2007. (18:31:01)
Postovi: (6)16
|
 Postano: 18:49 sri, 21. 2. 2007 Naslov: Teorem o postojanju i jedinstvenosti rjesenja dif.jedn. Postano: 18:49 sri, 21. 2. 2007 Naslov: Teorem o postojanju i jedinstvenosti rjesenja dif.jedn. |
    |
|
|
Dokaz koji imam zapocinje sa nekakvim diferencijalom wronskijana, i matricom koja pretezito ima nule i jedinice (na glavnoj dijagonali nule, na 'dijagonali' odmah iznad glavne same jedinice), s tim sto joj je u zadnjem retku niz koeficijenata a[size=9]i[/size] s minusima (koeficijenti iz samog izraza za diferencijalnu jednadzbu n-tog reda).
Ideja dokaza mi je potpuno nejasna :? . Otkud se stvorila ta matrica? Sto dobijemo kad integriramo wronskijan? Na kraju dolazimo do neke rekurzije sa wronksijanima za koju se uzme da konvergira i time je dokaz gotov jer nam je 'cilj bio pokazati da postoji limes niza funkcija (kojih funkcija? :roll: ) i da je taj limes rjesenje.
Na wikipediji je to pod 'Picard–Lindelöf theorem' ( http://en.wikipedia.org/wiki/Picard-Lindel%C3%B6f_theorem ), ali onaj dokaz mi je potpuno beskoristan (gotov u dva reda i nista ne pise konkretno).
Inace sam s fizickog odsjeka, a dokaz teorema mi treba za usmeni iz matematickih metoda fizike, a na mom forumu nitko nista ne zna :).
(Pa, ako se nadje neka dobra dusa koja ima volje pojasniti mi ovaj dokaz, nek uzme u obzir da nisam s matematike :) )
vjecno zahvalna:)
p.s. nadam se da nisam fulala predmet:) ako jesam, isprike moderatorima
Dokaz koji imam zapocinje sa nekakvim diferencijalom wronskijana, i matricom koja pretezito ima nule i jedinice (na glavnoj dijagonali nule, na 'dijagonali' odmah iznad glavne same jedinice), s tim sto joj je u zadnjem retku niz koeficijenata ai s minusima (koeficijenti iz samog izraza za diferencijalnu jednadzbu n-tog reda).
Ideja dokaza mi je potpuno nejasna  . Otkud se stvorila ta matrica? Sto dobijemo kad integriramo wronskijan? Na kraju dolazimo do neke rekurzije sa wronksijanima za koju se uzme da konvergira i time je dokaz gotov jer nam je 'cilj bio pokazati da postoji limes niza funkcija (kojih funkcija? . Otkud se stvorila ta matrica? Sto dobijemo kad integriramo wronskijan? Na kraju dolazimo do neke rekurzije sa wronksijanima za koju se uzme da konvergira i time je dokaz gotov jer nam je 'cilj bio pokazati da postoji limes niza funkcija (kojih funkcija?  ) i da je taj limes rjesenje. ) i da je taj limes rjesenje.
Na wikipediji je to pod 'Picard–Lindelöf theorem' ( http://en.wikipedia.org/wiki/Picard-Lindel%C3%B6f_theorem ), ali onaj dokaz mi je potpuno beskoristan (gotov u dva reda i nista ne pise konkretno).
Inace sam s fizickog odsjeka, a dokaz teorema mi treba za usmeni iz matematickih metoda fizike, a na mom forumu nitko nista ne zna  . .
(Pa, ako se nadje neka dobra dusa koja ima volje pojasniti mi ovaj dokaz, nek uzme u obzir da nisam s matematike  ) )
vjecno zahvalna:)
p.s. nadam se da nisam fulala predmet:) ako jesam, isprike moderatorima
|
|
| [Vrh] |
|
Adelaide
Forumaš(ica)

Pridružen/a: 21. 02. 2007. (18:31:01)
Postovi: (6)16
|
|
| [Vrh] |
|
pecina
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (14:15:23)
Postovi: (157)16
Spol: 
Lokacija: Happily traveling through space since 1986!
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 20:26 sri, 21. 2. 2007 Naslov: Postano: 20:26 sri, 21. 2. 2007 Naslov: |
    |
|
|
Picardov teorem (lokalni teorem o egzistenciji rjesenja) glasi :
Neka je [latex]P:=\{ (x,y)\in\mathbb{R}^2 |a_x<x<b_x,a_u<u<b_u \} , (x_0,u_0)\in P[/latex] ,te neka je [latex]f\in C(P) [/latex] , Lipschitova po 2 varijabli .Tada [latex]\exist \delta>0,t.d. ,I_{\delta}:=<x_0-\delta,x_0+\delta>\subset<a_x,b_x>[/latex] i inicijalni problem ima jednistveno rjesenje na [latex]I_{\delta}[/latex] (,te je rjesnje dano [latex]u(x)=u_0+\int_{x_0}^{x}f(s,u(s))ds[/latex] ) .Teorem se moze jednostavno poopciti.
Ako hoces dokaz vici! (no prilicno je dug) :(
U vezi lin. dif. jed n-tog reda,napisi sto te tocno zanima ,pa ti to (do sutra) napisem, ili ukoliko ti je hitno,posudi od prof.Alica Obicne diferencijalne jednadzbe ,prvo izdanje (!!!)
Picardov teorem (lokalni teorem o egzistenciji rjesenja) glasi :
Neka je 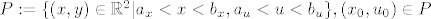 ,te neka je ,te neka je 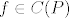 , Lipschitova po 2 varijabli .Tada , Lipschitova po 2 varijabli .Tada 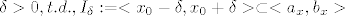 i inicijalni problem ima jednistveno rjesenje na i inicijalni problem ima jednistveno rjesenje na 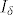 (,te je rjesnje dano (,te je rjesnje dano 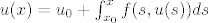 ) .Teorem se moze jednostavno poopciti. ) .Teorem se moze jednostavno poopciti.
Ako hoces dokaz vici! (no prilicno je dug) 
U vezi lin. dif. jed n-tog reda,napisi sto te tocno zanima ,pa ti to (do sutra) napisem, ili ukoliko ti je hitno,posudi od prof.Alica Obicne diferencijalne jednadzbe ,prvo izdanje (!!!)
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
Adelaide
Forumaš(ica)

Pridružen/a: 21. 02. 2007. (18:31:01)
Postovi: (6)16
|
 Postano: 22:28 sri, 21. 2. 2007 Naslov: Postano: 22:28 sri, 21. 2. 2007 Naslov: |
    |
|
|
[quote="Mr.Doe"]... te je rjesnje dano [latex]u(x)=u_0+\int_{x_0}^{x}f(s,u(s))ds[/latex][/quote]
Umjesto tvoje funkcije u(x) ja imam W(x) tj. W=vektor stupac sa y [size=9]i[/size] , i=1,n-1 gdje je y1=y, y2=y', y3=y''... y[size=9]n[/size]=y^(n-1) - ali dokaz zavrsava tako nekako, da. Odnosno treba doci do rekurzije:
[latex]Wn(x)=W_o+\int_{t_0}^{t}A(s)W(n-1)(s)ds[/latex]
(n i n-1 su indeksi)
Sto se tice Frobeniusove matrice koju je kolega spomenuo, mislim da je to tocno ono sto mi treba - ovaj Picardov teorem mi se ipak cini malo previse opcenit - meni treba dokaz da diferencijalna (linearna, n-tog reda) jednadzba ima rjesenje (i da je jedinstveno).
Dokaz prvenstveno moram prepricati, tako da nije potrebno previse tehnikalija. I ne pitam ja zapravo previse pametno pitanje:), nego zasto dokaz bas zapocinjemo sa d/dx(W)=AW gdje je A ta Frobeniusova matrica (a kako smo dosli do te matrice :roll: ?), a W gore spomenuti vektor stupac, pa to integriramo - zasto ce to bas dati niz funkcija ciji limes je rjesenje?
U medjuvremenu sam pogledala u biljeske i otkrila zapravo da mi je pod Picardovim teoremom 'da u svakoj neposrednoj okolini bitnog singulariteta funkcija poprima sve vrijednosti osim najvise jedne' - pa ste me sad zbunili malo, jesam li to nesto krivo oznacila?
| Mr.Doe (napisa): | ... te je rjesnje dano 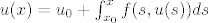 |
Umjesto tvoje funkcije u(x) ja imam W(x) tj. W=vektor stupac sa y i , i=1,n-1 gdje je y1=y, y2=y', y3=y''... yn=y^(n-1) - ali dokaz zavrsava tako nekako, da. Odnosno treba doci do rekurzije:
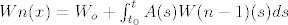
(n i n-1 su indeksi)
Sto se tice Frobeniusove matrice koju je kolega spomenuo, mislim da je to tocno ono sto mi treba - ovaj Picardov teorem mi se ipak cini malo previse opcenit - meni treba dokaz da diferencijalna (linearna, n-tog reda) jednadzba ima rjesenje (i da je jedinstveno).
Dokaz prvenstveno moram prepricati, tako da nije potrebno previse tehnikalija. I ne pitam ja zapravo previse pametno pitanje:), nego zasto dokaz bas zapocinjemo sa d/dx(W)=AW gdje je A ta Frobeniusova matrica (a kako smo dosli do te matrice  ?), a W gore spomenuti vektor stupac, pa to integriramo - zasto ce to bas dati niz funkcija ciji limes je rjesenje? ?), a W gore spomenuti vektor stupac, pa to integriramo - zasto ce to bas dati niz funkcija ciji limes je rjesenje?
U medjuvremenu sam pogledala u biljeske i otkrila zapravo da mi je pod Picardovim teoremom 'da u svakoj neposrednoj okolini bitnog singulariteta funkcija poprima sve vrijednosti osim najvise jedne' - pa ste me sad zbunili malo, jesam li to nesto krivo oznacila?
|
|
| [Vrh] |
|
|






