|
Broj rjesenja X(n) diofantske jednadzbe:
[latex]a^2+b^2+c^2+d^2=n[/latex]
(gdje su a,b,c,d pozitivni prirodni brojevi) dan je sa:
[latex]X(n)=8*\sum_{d4}[/latex]
gdje [latex]\sum_{d4}[/latex] oznacava sumu djelitelja on n koji NISU djeljivi sa 4.
Gledamo sumu:
[latex]H(n)=\displaystyle\sum_{i=1}^n \frac{X(i)}{i}[/latex]
Kada n pustimo da raste H(n) je sve "bolje" aproksimirana vrijednoscu[latex]n*\pi^2[/latex].
Promatram sada:
[latex]L(n)=H(n)-n*\pi^2[/latex]
Izgleda da je :
[latex]L(n)=C+\sum[/latex] [b]~[/b].
Gdje je [latex]\sum[/latex][b]~[/b] suma periodickih funkcija ,a [latex]C[/latex] je konstanta za koju numericki dobivam da je -0.61...
Moze li mi netko pomoci /uputiti me da izvedem/nadjem izraz za [b]C[/b]
ako je spektar [b]L(n)[/b],sto pretpotpostavljam da je,povezan sa nulama Riemannove zeta funkcije?
Mozda je taj izraz vec odavno poznat i izveden,ali ja nemam informacije o tome.Molio bih specjaliste za teoriju brojeva da pomognu.
Hvala,
Zvonimir
Broj rjesenja X(n) diofantske jednadzbe:
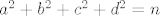
(gdje su a,b,c,d pozitivni prirodni brojevi) dan je sa:
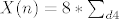
gdje 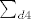 oznacava sumu djelitelja on n koji NISU djeljivi sa 4.
Gledamo sumu:
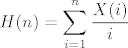
Kada n pustimo da raste H(n) je sve "bolje" aproksimirana vrijednoscu .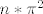
Promatram sada:
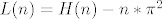
Izgleda da je :
 ~.
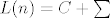Gdje je 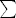 ~ suma periodickih funkcija ,a  je konstanta za koju numericki dobivam da je -0.61...
Moze li mi netko pomoci /uputiti me da izvedem/nadjem izraz za C
ako je spektar L(n),sto pretpotpostavljam da je,povezan sa nulama Riemannove zeta funkcije?
Mozda je taj izraz vec odavno poznat i izveden,ali ja nemam informacije o tome.Molio bih specjaliste za teoriju brojeva da pomognu.
Hvala,
Zvonimir
|
.