| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 22:29 pet, 9. 2. 2007 Naslov: Numeričke metode financijske matematike Postano: 22:29 pet, 9. 2. 2007 Naslov: Numeričke metode financijske matematike |
    |
|
|
spremam se za nmfm, pa me zanima je li uopce postoje materijali iz vjezbi s tog kolegija (naime radilo se na kompovima, a ispit pisemo pismeno?!) Odakle bi bilo najpametnije uciti za pismeni? Bila sam i u knjiznici, al nema nikakve zbirke, imam biljeske s predavanja, ali to mi bas i ne pomaze. nije mi jasno, zasto se na vjezbama zadaci programiraju u matlabu, ako nam za ispit treba nesto sasvim drugo?
spremam se za nmfm, pa me zanima je li uopce postoje materijali iz vjezbi s tog kolegija (naime radilo se na kompovima, a ispit pisemo pismeno?!) Odakle bi bilo najpametnije uciti za pismeni? Bila sam i u knjiznici, al nema nikakve zbirke, imam biljeske s predavanja, ali to mi bas i ne pomaze. nije mi jasno, zasto se na vjezbama zadaci programiraju u matlabu, ako nam za ispit treba nesto sasvim drugo?
|
|
| [Vrh] |
|
Gost
|
 Postano: 13:36 uto, 27. 2. 2007 Naslov: zdaci za pismeni iz nmfm Postano: 13:36 uto, 27. 2. 2007 Naslov: zdaci za pismeni iz nmfm |
    |
|
|
dakle prvo nabavis odgovarajuce pismene, ovisno o tome kad je kolegij odslusan. onda nades neke dobre biljeske s vjezbi iz nmfm, iz predavanja takoder, i jos biljeznicu iz vjezbi sa uvoda u numericku matematiku. iskombiniras to troje i porjesavas 5 rokova i to je to. uvijek je neka interpolacija, neka metoda za nalazenje nultocke, jedan teoretski zadatak/tipa-objasni/, odj obicna i odj rubni problem. sretno.
dakle prvo nabavis odgovarajuce pismene, ovisno o tome kad je kolegij odslusan. onda nades neke dobre biljeske s vjezbi iz nmfm, iz predavanja takoder, i jos biljeznicu iz vjezbi sa uvoda u numericku matematiku. iskombiniras to troje i porjesavas 5 rokova i to je to. uvijek je neka interpolacija, neka metoda za nalazenje nultocke, jedan teoretski zadatak/tipa-objasni/, odj obicna i odj rubni problem. sretno.
|
|
| [Vrh] |
|
ninocka
Forumaš(ica)

Pridružen/a: 15. 04. 2004. (16:03:44)
Postovi: (3D)16
Lokacija: ne drzi me mjesto
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
 Postano: 20:46 čet, 22. 3. 2007 Naslov: Postano: 20:46 čet, 22. 3. 2007 Naslov: |
    |
|
|
Nova asistentica je Martina Barberic (iliti ja). Moj e-mail je tipa ime.prezime (AT) math.hr
Dakle, kolegij se polaze kolokvijima. Bit ce dva kolokvija, svaki nosi 50 bodova.
Moci ce se raznoraznim aktivnostima (npr. zadacama) prikupiti dodatnih 10 bodova.
Medjutim, ti se dodatni bodovi mogu iskoristiti samo ako student na kolokvijima prikupi barem 45 bodova. Drugim rijecima, ako na kolokvijima prikupite 35 bodova i na vjezbama jos dodatnih 10 bodova, necete proci.
Uvjerenja sam da osoba koja nije redovito na vjezbama ne moze znati sto je za zadacu, niti je rijesiti pa preporucam onima koji misle skupiti dodatne bodove da dolaze na vjezbe.
Kad se vec ovako oglasavam, odmah da rascistimo jednu zabludu.
Kolegij se zove Numericke metode u financijskoj matematici, a ne Praktikum/Uvod u MATLAB. On nam sluzi samo kao pomocno sredstvo - kada se kaze 'Ova mreza interpolacije je bolja od one.', MATLAB uskace da nam graficki na nekom primjeru prikaze da ta tvrdnja stoji.
U idealnom svijetu, grupe bi bile barem dvostruko manje i kolokviji bi se mogli drzati u praktikumu, uz pomoc MATLABa. Medjutim, svijet nije idealan pa se kolokviji pisu na papiru.
Nova asistentica je Martina Barberic (iliti ja). Moj e-mail je tipa ime.prezime (AT) math.hr
Dakle, kolegij se polaze kolokvijima. Bit ce dva kolokvija, svaki nosi 50 bodova.
Moci ce se raznoraznim aktivnostima (npr. zadacama) prikupiti dodatnih 10 bodova.
Medjutim, ti se dodatni bodovi mogu iskoristiti samo ako student na kolokvijima prikupi barem 45 bodova. Drugim rijecima, ako na kolokvijima prikupite 35 bodova i na vjezbama jos dodatnih 10 bodova, necete proci.
Uvjerenja sam da osoba koja nije redovito na vjezbama ne moze znati sto je za zadacu, niti je rijesiti pa preporucam onima koji misle skupiti dodatne bodove da dolaze na vjezbe.
Kad se vec ovako oglasavam, odmah da rascistimo jednu zabludu.
Kolegij se zove Numericke metode u financijskoj matematici, a ne Praktikum/Uvod u MATLAB. On nam sluzi samo kao pomocno sredstvo - kada se kaze 'Ova mreza interpolacije je bolja od one.', MATLAB uskace da nam graficki na nekom primjeru prikaze da ta tvrdnja stoji.
U idealnom svijetu, grupe bi bile barem dvostruko manje i kolokviji bi se mogli drzati u praktikumu, uz pomoc MATLABa. Medjutim, svijet nije idealan pa se kolokviji pisu na papiru.
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 17:10 uto, 3. 4. 2007 Naslov: Postano: 17:10 uto, 3. 4. 2007 Naslov: |
    |
|
|
U 5.zadatku trazimo nultocke fije [latex]f(y)=\sum_{t=1}^{N}\frac{c_t}{(1+y)^t}-p[/latex] ,te buduci da je [latex]f'(y)<0[/latex] ,tvrdimo da je [latex]\alpha [/latex], nultocka fije.
No,zasto je to tako??
Npr. pogledajmo f-ij [latex]-\arctan (x)+\pi[/latex] je stogo padajuca na [latex]\mathbb{R}[/latex] , ali nema niti jednu nultocku.
Dakle,osim ako [latex]f(x)f(y)<0[/latex] za neki [latex]x,y[/latex], ne mozemo govoriti o nultocki fije.
Mozete li mi to pojasniti?
U 5.zadatku trazimo nultocke fije 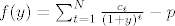 ,te buduci da je ,te buduci da je 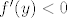 ,tvrdimo da je ,tvrdimo da je  , nultocka fije. , nultocka fije.
No,zasto je to tako??
Npr. pogledajmo f-ij 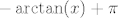 je stogo padajuca na je stogo padajuca na  , ali nema niti jednu nultocku. , ali nema niti jednu nultocku.
Dakle,osim ako 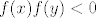 za neki za neki 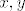 , ne mozemo govoriti o nultocki fije. , ne mozemo govoriti o nultocki fije.
Mozete li mi to pojasniti?
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 13:47 sri, 4. 4. 2007 Naslov: Postano: 13:47 sri, 4. 4. 2007 Naslov: |
    |
|
|
Ok! Dakle,ako postoji onda je jednostruka.
Jos jedno pitanje:
U matlabu zelim naci nultocku fije, te hocu pokrenuti newton.m ,no kada upisujem fiju i pripadnu prvu derivaciju stalno mi javlja;
??? Undefined function or variable 'x'.
Upisujem newton(1000/(1+x)*(10+15/(1+x)+12/(1+x)^2+15/(1+x)^3+7/(1+x)^4)-49095.03,-1000/(1+x)^2*(10+30/(1+x)+36/(1+x)^2+60/(1+x)^3+35/(1+x)^4),0.07,e-15,5.77255e+5,9.283211e+4)
Mozete li mi reci u cemu grijesim?
Hvala!
Ok! Dakle,ako postoji onda je jednostruka.
Jos jedno pitanje:
U matlabu zelim naci nultocku fije, te hocu pokrenuti newton.m ,no kada upisujem fiju i pripadnu prvu derivaciju stalno mi javlja;
??? Undefined function or variable 'x'.
Upisujem newton(1000/(1+x)*(10+15/(1+x)+12/(1+x)^2+15/(1+x)^3+7/(1+x)^4)-49095.03,-1000/(1+x)^2*(10+30/(1+x)+36/(1+x)^2+60/(1+x)^3+35/(1+x)^4),0.07,e-15,5.77255e+5,9.283211e+4)
Mozete li mi reci u cemu grijesim?
Hvala!
|
|
| [Vrh] |
|
Perosito
Forumaš(ica)

Pridružen/a: 30. 01. 2004. (22:21:16)
Postovi: (7E)16
|
 Postano: 14:08 sri, 4. 4. 2007 Naslov: Postano: 14:08 sri, 4. 4. 2007 Naslov: |
    |
|
|
Probaj upisat sljedeće (samo izmjeniš path):
path(path,'C:\Documents and Settings\Pero\Desktop\FAKS\Num. metode u financijskoj matematici')
f=fcnchk('10000/(1+x)+15000/(1+x)^2+12000/(1+x)^3+15000/(1+x)^4+7000/(1+x)^5-49095.03');
df=fcnchk('-10000/(1+x)^2-2*15000/(1+x)^3-3*12000/(1+x)^4-4*15000/(1+x)^5-5*7000/(1+x)^6');
[x,n]=newton(f,df,0.07,1e-15,9.283211e+4,5.77255e+5)
Ja sam tak upisal i izbacilo mi je x=0.667, n=3
A možeš i ovak:
path(path,'C:\Documents and Settings\Pero\Desktop\FAKS\Num. metode u financijskoj matematici')
[x,n]=newton('10000/(1+x)+15000/(1+x)^2+12000/(1+x)^3+15000/(1+x)^4+7000/(1+x)^5-49095.03','-10000/(1+x)^2-2*15000/(1+x)^3-3*12000/(1+x)^4-4*15000/(1+x)^5-5*7000/(1+x)^6',0.07,1e-15,9.283211e+4,5.77255e+5)
Razlika je kaj ja imam tu navodnike (ti ih gore nemaš)
Probaj upisat sljedeće (samo izmjeniš path):
path(path,'C:\Documents and Settings\Pero\Desktop\FAKS\Num. metode u financijskoj matematici')
f=fcnchk('10000/(1+x)+15000/(1+x)^2+12000/(1+x)^3+15000/(1+x)^4+7000/(1+x)^5-49095.03');
df=fcnchk('-10000/(1+x)^2-2*15000/(1+x)^3-3*12000/(1+x)^4-4*15000/(1+x)^5-5*7000/(1+x)^6');
[x,n]=newton(f,df,0.07,1e-15,9.283211e+4,5.77255e+5)
Ja sam tak upisal i izbacilo mi je x=0.667, n=3
A možeš i ovak:
path(path,'C:\Documents and Settings\Pero\Desktop\FAKS\Num. metode u financijskoj matematici')
[x,n]=newton('10000/(1+x)+15000/(1+x)^2+12000/(1+x)^3+15000/(1+x)^4+7000/(1+x)^5-49095.03','-10000/(1+x)^2-2*15000/(1+x)^3-3*12000/(1+x)^4-4*15000/(1+x)^5-5*7000/(1+x)^6',0.07,1e-15,9.283211e+4,5.77255e+5)
Razlika je kaj ja imam tu navodnike (ti ih gore nemaš)
_________________ Nije sve tako sivo... Kad imaš s nekim otić na pivo  |
|
| [Vrh] |
|
Marinchi
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
hexy
Forumaš(ica)

Pridružen/a: 19. 11. 2002. (09:39:35)
Postovi: (8A)16
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
 Postano: 10:02 ned, 29. 4. 2007 Naslov: Postano: 10:02 ned, 29. 4. 2007 Naslov: |
    |
|
|
Iskazi teorema vam nece biti potrebni. Smijete imati sve formule koje smo radili na vjezbama.
No, imajte na umu da cu, buduci da se kolokvij pise 120 minuta, imati sasvim dovoljno vremena da pregledam dobar dio vasih formula. Medju formulama ne smije biti rijesenih zadataka.
Na kolokviju mozete skupiti 50 bodova. Na koliko ce zadataka i kako tih 50 bodova biti raspodijeljeno, jos se ne zna, a nije niti bitno. Bitno je da cete imati sasvim dovoljno vremena da rijesite te zadatke. Buduci da smijete imati formule, a zadaci se rjesavaju po nekom algoritmu, bit ce bitno da su brojke koje dobijete tocne.
Programabilni kalkulatori su zabranjeni. Za one koji ne znaju, pismeni se nalaze na [url]http://web.math.hr/~nela/nmfm.html[/url]
Iskazi teorema vam nece biti potrebni. Smijete imati sve formule koje smo radili na vjezbama.
No, imajte na umu da cu, buduci da se kolokvij pise 120 minuta, imati sasvim dovoljno vremena da pregledam dobar dio vasih formula. Medju formulama ne smije biti rijesenih zadataka.
Na kolokviju mozete skupiti 50 bodova. Na koliko ce zadataka i kako tih 50 bodova biti raspodijeljeno, jos se ne zna, a nije niti bitno. Bitno je da cete imati sasvim dovoljno vremena da rijesite te zadatke. Buduci da smijete imati formule, a zadaci se rjesavaju po nekom algoritmu, bit ce bitno da su brojke koje dobijete tocne.
Programabilni kalkulatori su zabranjeni. Za one koji ne znaju, pismeni se nalaze na http://web.math.hr/~nela/nmfm.html
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|



