| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Mr.Doe
Forumaš(ica)
Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 14:02 pon, 30. 4. 2007 Naslov: DZ4 - pitanja |
    |
|
|
Mozemo li dobiti hint kako dokazati da ne postoji blok dizajn s parametrima (53,13,3) (zadatak 5) ? Imajte na umu da nisam slusao teoriju brojeva. 8) .
Te u prvom zadatku,kako da napisemo matricu incidencije , tj. dobio sam sve blokove ,no zbunjujem me to sto su blokovi u [latex]\mathbb{Z}_4 \times \mathbb{Z}_4[/latex] (tj. tocke tih blokova ).
Unaprijed hvala.
Mozemo li dobiti hint kako dokazati da ne postoji blok dizajn s parametrima (53,13,3) (zadatak 5) ? Imajte na umu da nisam slusao teoriju brojeva.  .
Te u prvom zadatku,kako da napisemo matricu incidencije , tj. dobio sam sve blokove ,no zbunjujem me to sto su blokovi u 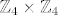 (tj. tocke tih blokova ).
Unaprijed hvala.
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo
Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
| Postano: 22:34 pon, 30. 4. 2007 Naslov: Re: DZ4 - pitanja |
|
|
|
[quote="Mr.Doe"]Mozemo li dobiti hint kako dokazati da ne postoji blok dizajn s parametrima (53,13,3) (zadatak 5) ? Imajte na umu da nisam slusao teoriju brojeva. 8) .[/quote]
Napisi diofantsku jednadzbu od BRC teorema. Dokazi da, ako je (x,y,z) cjelobrojno rjesenje, onda je i (x/5,y/5,z/5) => mora biti (x,y,z)=(0,0,0) jer bismo u suprotnom prije ili kasnije dobili razlomke. Ili samo provjeri uvjete Tm. 2.24 na str. 37 knjige.
[quote="Mr.Doe"]Te u prvom zadatku,kako da napisemo matricu incidencije , tj. dobio sam sve blokove ,no zbunjujem me to sto su blokovi u [latex]\mathbb{Z}_4 \times \mathbb{Z}_4[/latex] (tj. tocke tih blokova ).
[/quote]
Pa sta ima veze? Reci su oznaceni tockama, tj. uredjenim parovima, stupci blokovima. Gdje tocka pripada bloku stavi 1, a na ostala mjesta 0.
| Mr.Doe (napisa): | | Mozemo li dobiti hint kako dokazati da ne postoji blok dizajn s parametrima (53,13,3) (zadatak 5) ? Imajte na umu da nisam slusao teoriju brojeva. . |
Napisi diofantsku jednadzbu od BRC teorema. Dokazi da, ako je (x,y,z) cjelobrojno rjesenje, onda je i (x/5,y/5,z/5) ⇒ mora biti (x,y,z)=(0,0,0) jer bismo u suprotnom prije ili kasnije dobili razlomke. Ili samo provjeri uvjete Tm. 2.24 na str. 37 knjige.
| Mr.Doe (napisa): | Te u prvom zadatku,kako da napisemo matricu incidencije , tj. dobio sam sve blokove ,no zbunjujem me to sto su blokovi u 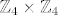(tj. tocke tih blokova ).
|
Pa sta ima veze? Reci su oznaceni tockama, tj. uredjenim parovima, stupci blokovima. Gdje tocka pripada bloku stavi 1, a na ostala mjesta 0.
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)
Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo
Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Daya
Forumaš(ica)
Pridružen/a: 20. 02. 2006. (02:00:09)
Postovi: (2F)16
Spol: 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo
Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|
