| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ß
Forumaš(ica)
Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
 Postano: 18:06 čet, 17. 5. 2007 Naslov: Anihilator anihilatora Postano: 18:06 čet, 17. 5. 2007 Naslov: Anihilator anihilatora |
    |
|
|
Danas smo na vjezbama iz LA2 dokazali da je za neki potprostor M, ortogonalni komplement ortogonalnog komplementa opet pocetni potprostor.
Prof. je stalno povlacio usporedbe s anihilatorima, pa je postavio i pitanje da li isto vrijedi za anihilatore, dakle da li za proizvoljni M potprostor od V, vrijedi: [latex](M^0)^0 = M[/latex] , te rekao da o tome razmislimo...
Razmisljali smo dosta i nismo zakljucili nista pametno. :(
Moje je misljenje da stvar ne vrijedi.
Naime, [latex](M^0)^0 \leq (V^*)^*[/latex], a ocito [latex](V^*)^* \neq V[/latex] ..
Mislim, radi se o razlicitim objektima: anihilator anihilatora je vektorski prostor ciji su vektori "funkcije nad funkcijama nad vektorima iz M", dok su vektori iz M... pa, vektori iz M :P :lol:
Sad, kolegica citira knjigu prof. Horvatica:
"Ako je M potprostor od konacnodimenzionalnog v.p., onda je [latex](M^0)^0 = M[/latex] (jednakost u smislu konvencije o identifikaciji)"
:shock:
Nemam pojma sto je konvencija o identifikaciji ...
:?
Svaka pomoc je dobrodosla ! :)
Danas smo na vjezbama iz LA2 dokazali da je za neki potprostor M, ortogonalni komplement ortogonalnog komplementa opet pocetni potprostor.
Prof. je stalno povlacio usporedbe s anihilatorima, pa je postavio i pitanje da li isto vrijedi za anihilatore, dakle da li za proizvoljni M potprostor od V, vrijedi: 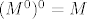 , te rekao da o tome razmislimo... , te rekao da o tome razmislimo...
Razmisljali smo dosta i nismo zakljucili nista pametno. 
Moje je misljenje da stvar ne vrijedi.
Naime, 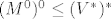 , a ocito , a ocito 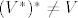 .. ..
Mislim, radi se o razlicitim objektima: anihilator anihilatora je vektorski prostor ciji su vektori "funkcije nad funkcijama nad vektorima iz M", dok su vektori iz M... pa, vektori iz M  
Sad, kolegica citira knjigu prof. Horvatica:
"Ako je M potprostor od konacnodimenzionalnog v.p., onda je 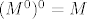 (jednakost u smislu konvencije o identifikaciji)" (jednakost u smislu konvencije o identifikaciji)"

Nemam pojma sto je konvencija o identifikaciji ...

Svaka pomoc je dobrodosla ! 
_________________
Devious movements in your eyes moved me from relief
Breath comes out white clouds with your lies
and filters through me
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
 Postano: 20:14 čet, 17. 5. 2007 Naslov: Postano: 20:14 čet, 17. 5. 2007 Naslov: |
    |
|
|
Mozda ova skica... neka je cijela prica konacnodimenzionalna:
[*] Bidual [latex](V^*)^*[/latex] je izomorfan s [latex]V[/latex]:
[latex](\forall v\in V)[/latex] definiramo "evaluator" [latex]\hat{v}\in(V^*)^*[/latex] kao [latex]\hat{v}(f)\stackrel{\mathsf{def}}{=}f(v)[/latex].
Neka su [latex]m\in M,f\in M^0[/latex] proizvoljni.
Tada vrijedi [latex]\hat{m}(f)=f(m)=0[/latex], pa [latex]\hat{m}\in(M^0)^0[/latex].
[latex]M[/latex] je izomorfan s [latex](M^*)^*[/latex], prema [*].
S druge strane, [latex](M^*)^*[/latex] je iste dimenzije kao i [latex](M^0)^0[/latex], pa gornji paragraf u biti opisuje izomorfizam [latex]M[/latex] i [latex](M^0)^0[/latex].
Mozda ova skica... neka je cijela prica konacnodimenzionalna:
[*] Bidual 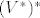 je izomorfan s je izomorfan s 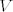 : :
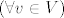 definiramo "evaluator" definiramo "evaluator" 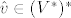 kao kao 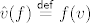 . .
Neka su 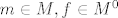 proizvoljni. proizvoljni.
Tada vrijedi 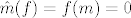 , pa , pa 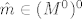 . .
 je izomorfan s je izomorfan s 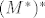 , prema [*]. , prema [*].
S druge strane, 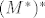 je iste dimenzije kao i je iste dimenzije kao i 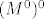 , pa gornji paragraf u biti opisuje izomorfizam , pa gornji paragraf u biti opisuje izomorfizam  i i 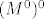 . .
|
|
| [Vrh] |
|
ß
Forumaš(ica)

Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
 Postano: 20:42 čet, 17. 5. 2007 Naslov: Postano: 20:42 čet, 17. 5. 2007 Naslov: |
    |
|
|
[quote="venovako"]Mozda ova skica... neka je cijela prica konacnodimenzionalna (...)[/quote]
Ako je V konacne dimenzije:
Vrijedi [latex]dim(M^0) = dim(V) - dim(M)[/latex], pa onda i
[latex]dim(M^0)^0 = dim(V) - dim(M^0)=[/latex][latex] dim(V)-(dim(V)-dim(M))=dim(M)[/latex]
Dakle prostori [latex]M[/latex] i [latex](M^0)^0[/latex] su iste dimenzije, pa su prema tome i izomorfni...
Medjutim to jos nista ne govori o i jednakosti tih vektorskih prostora...
@venovako: da li to znaci da bi "jednakost u smislu konvencije o identifikaciji" trebala biti samo postojanje izomorfizma, a ne "prava" jednakost, u smislu skupovne jednakosti?
Jer, da me ubijes, ne mogu dokazat ni [latex](M^0)^0\subset M[/latex] niti obrnutu inkluziju... :?
A i intuicija mi govori da jednakost ne vrijedi..
:P
| venovako (napisa): | | Mozda ova skica... neka je cijela prica konacnodimenzionalna (...) |
Ako je V konacne dimenzije:
Vrijedi 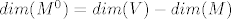 , pa onda i , pa onda i
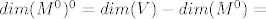 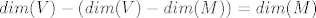
Dakle prostori  i i 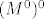 su iste dimenzije, pa su prema tome i izomorfni... su iste dimenzije, pa su prema tome i izomorfni...
Medjutim to jos nista ne govori o i jednakosti tih vektorskih prostora...
@venovako: da li to znaci da bi "jednakost u smislu konvencije o identifikaciji" trebala biti samo postojanje izomorfizma, a ne "prava" jednakost, u smislu skupovne jednakosti?
Jer, da me ubijes, ne mogu dokazat ni 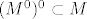 niti obrnutu inkluziju... niti obrnutu inkluziju... 
A i intuicija mi govori da jednakost ne vrijedi..

_________________
Devious movements in your eyes moved me from relief
Breath comes out white clouds with your lies
and filters through me
Zadnja promjena: ß; 11:04 pet, 18. 5. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Gost
|
 Postano: 23:01 čet, 17. 5. 2007 Naslov: Postano: 23:01 čet, 17. 5. 2007 Naslov: |
    |
|
|
Doista ne vrijedi "doslovna" jednakost, ali vrijedi izomorfizam i to
posebne vrste, kanonski izomorfizam, koji se odlikuje time da se
može definirati bez posredstva baze (na način kako je objasnio
venovako). Dakle, kanonski ili prirodni izomorfizam, i onda je
uobičajeno identificirati vektore s elementima biduala.
Doista ne vrijedi "doslovna" jednakost, ali vrijedi izomorfizam i to
posebne vrste, kanonski izomorfizam, koji se odlikuje time da se
može definirati bez posredstva baze (na način kako je objasnio
venovako). Dakle, kanonski ili prirodni izomorfizam, i onda je
uobičajeno identificirati vektore s elementima biduala.
|
|
| [Vrh] |
|
ß
Forumaš(ica)

Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
 Postano: 11:12 pet, 18. 5. 2007 Naslov: Postano: 11:12 pet, 18. 5. 2007 Naslov: |
    |
|
|
[quote="Anonymous"]Doista ne vrijedi "doslovna" jednakost, ali vrijedi izomorfizam i to
posebne vrste, kanonski izomorfizam, koji se odlikuje time da se
može definirati bez posredstva baze (na način kako je objasnio
venovako). Dakle, kanonski ili prirodni izomorfizam, i onda je
uobičajeno identificirati vektore s elementima biduala.[/quote]
Ok sad shvaćam! Neka vrsta jednakosti dakle ipak postoji, ali nije "prava"... :lol:
Hvala venovako & gostu! 8)
| Anonymous (napisa): | Doista ne vrijedi "doslovna" jednakost, ali vrijedi izomorfizam i to
posebne vrste, kanonski izomorfizam, koji se odlikuje time da se
može definirati bez posredstva baze (na način kako je objasnio
venovako). Dakle, kanonski ili prirodni izomorfizam, i onda je
uobičajeno identificirati vektore s elementima biduala. |
Ok sad shvaćam! Neka vrsta jednakosti dakle ipak postoji, ali nije "prava"... 
Hvala venovako & gostu! 
_________________
Devious movements in your eyes moved me from relief
Breath comes out white clouds with your lies
and filters through me
|
|
| [Vrh] |
|
|







