|
Treba pokazati da ako [latex]||x_n||_1\rightarrow 0 \Leftrightarrow ||x_n||_2\rightarrow 0[/latex] gdje su to proizvoljen norme na [latex]\mathbb{R}^k[/latex]. Pretpostavimo da [latex]||\sum a_i ^{(n)}e_i||_\infty \rightarrow 0[/latex] , tj. [latex]a_i ^{(n)}\rightarrow 0 ,\forall i=1,\dots ,n[/latex], dakle uzeli smo da je jedna norma -beskonacno norma. Dakle imam [latex]||\sum a_i ^{(n)}e_i||_2 \leq \sum |a_i ^{(n)} ||e_i||_2 \rightarrow 0 [/latex] ,buduci da [latex]a_i ^{(n)}\rightarrow 0[/latex] (iskoristili smo nejednakost trokuta i homogenost norme) ,tj. pokazali smo jedan smjer. Pretpostavimo da vrijedi [latex]||\sum a_i ^{(n)} e_i ||_2\rightarrow 0[/latex]. Ako je beskonacno mnogo vektora u tom nizu koji su udaljeni od [latex]0[/latex] u [latex]|| \cdot ||_1[/latex] , mozemo slobodno (bmo) pretpostaviti da [latex]|a_1 ^{(n)}|=1\geq |a_i ^{(n)}|,\forall n \forall i[/latex] , dakle iz niza [latex](a_1 ^{(n)},\dots ,a_k ^{(n)})_n[/latex], mozemo naci podniz koji konvergira ka nekome [latex](a_1,\dots,a_k),|a_1|=1[/latex]. Pretpostavimo da citav niz konvegira ka tom limesu pa onda dobivamo [latex]||\sum (a_i ^{(n)}-a_i)e_i||_1\rightarrow 0[/latex], dok sa druge strane [latex] ||\sum (a_i ^{(n)}-a_i)e_i)||_2 \rightarrow 0[/latex] ,sto implicira da [latex]|a_i|=0,\forall i[/latex] ,sto je u suprotnosti da [latex]|a_1|=1[/latex].
Ima jos neki dokaz gdje se za jednu normu uzme eukliska norma i onda iz C-S-B nejednakosti dobi trazena konstanta, no koristi se Leb-Borel teorem i tvrdi se kompaktnost nekih prostora no to je prekomplicirano, i ne bih ulazio u dokazivanje tih tvrdnja.
Za drugo pitanje:da :D
[size=7]znam da je kasno, ali prije kolokvija si rekao da si to uspio dokazati, pa onda slobodno stavi svoj dokaz.[/size]
Treba pokazati da ako  gdje su to proizvoljen norme na gdje su to proizvoljen norme na 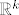 . Pretpostavimo da . Pretpostavimo da 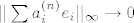 , tj. , tj. 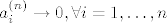 , dakle uzeli smo da je jedna norma -beskonacno norma. Dakle imam , dakle uzeli smo da je jedna norma -beskonacno norma. Dakle imam 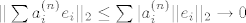 ,buduci da ,buduci da 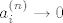 (iskoristili smo nejednakost trokuta i homogenost norme) ,tj. pokazali smo jedan smjer. Pretpostavimo da vrijedi (iskoristili smo nejednakost trokuta i homogenost norme) ,tj. pokazali smo jedan smjer. Pretpostavimo da vrijedi 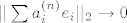 . Ako je beskonacno mnogo vektora u tom nizu koji su udaljeni od . Ako je beskonacno mnogo vektora u tom nizu koji su udaljeni od  u u 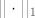 , mozemo slobodno (bmo) pretpostaviti da , mozemo slobodno (bmo) pretpostaviti da 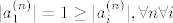 , dakle iz niza , dakle iz niza 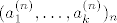 , mozemo naci podniz koji konvergira ka nekome , mozemo naci podniz koji konvergira ka nekome 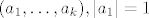 . Pretpostavimo da citav niz konvegira ka tom limesu pa onda dobivamo . Pretpostavimo da citav niz konvegira ka tom limesu pa onda dobivamo 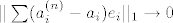 , dok sa druge strane , dok sa druge strane 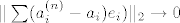 ,sto implicira da ,sto implicira da 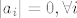 ,sto je u suprotnosti da ,sto je u suprotnosti da 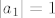 . .
Ima jos neki dokaz gdje se za jednu normu uzme eukliska norma i onda iz C-S-B nejednakosti dobi trazena konstanta, no koristi se Leb-Borel teorem i tvrdi se kompaktnost nekih prostora no to je prekomplicirano, i ne bih ulazio u dokazivanje tih tvrdnja.
Za drugo pitanje:da 
znam da je kasno, ali prije kolokvija si rekao da si to uspio dokazati, pa onda slobodno stavi svoj dokaz.
|







