| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
 Postano: 13:23 sub, 2. 6. 2007 Naslov: Postano: 13:23 sub, 2. 6. 2007 Naslov: |
    |
|
|
Hvala Luuka!!
To rješenje mi je riješilo još jedan problem!
Imam još jedno pitanje ako mi netko može pomoći:
Zadatak je odrediti na kojem je intervalu funkcija [latex]\displaystyle f(x)=\frac{1}{1+x^2} [/latex] konveksna?
Po definiciji funkcija f sa <a,b> u R je konveksna na intervalu <a,b> ako vrijedi za svake x_1,x_2 iz <a,b> da je
[latex]\displaystyle f(\frac{x_1+x_2}{2})\leq\frac{f(x_1)+f(x_2)}{2} [/latex]
E, kad sam ja sve uvrstio i izračunao (tko zna jesam li dobro) dobio sam da mora vrijediti
[latex] (x_1+x_2)^2+2(x_1x_2-1)\geq0 [/latex]
I kako sada odrediti interval??
Hvala Luuka!!
To rješenje mi je riješilo još jedan problem!
Imam još jedno pitanje ako mi netko može pomoći:
Zadatak je odrediti na kojem je intervalu funkcija 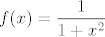 konveksna? konveksna?
Po definiciji funkcija f sa <a,b> u R je konveksna na intervalu <a,b> ako vrijedi za svake x_1,x_2 iz <a,b> da je
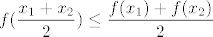
E, kad sam ja sve uvrstio i izračunao (tko zna jesam li dobro) dobio sam da mora vrijediti
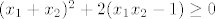
I kako sada odrediti interval??
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:37 sub, 2. 6. 2007 Naslov: Postano: 17:37 sub, 2. 6. 2007 Naslov: |
    |
|
|
Možda se može iz te tvoje jednadžbe nešt zaključit. Npr onaj kvadrat na početku je uvijek >=0 pa gledaš onaj drugi.
Sad kaže x1*x2>=1. Fja je uvijek pozitivna, domena je cijeli R pa ima dva slučaja.
Prvi je da su oba neg, drugi da su oba poz. Kad su pozitivni onda je x2>=1/x1, pošto je x1>0 (pozitivan) onda je x2 iz <0,1>. Dakle <x1,x2> je <0, +beskonačno>
Drugi slučaj analogno pa se dobije <-beskonačno,0>. U nuli je vrijednost fje 1, to je lok maximum pa je fja konvexna na cijelom R.
Valjda mi je dobra logika....
Možda se može iz te tvoje jednadžbe nešt zaključit. Npr onaj kvadrat na početku je uvijek >=0 pa gledaš onaj drugi.
Sad kaže x1*x2>=1. Fja je uvijek pozitivna, domena je cijeli R pa ima dva slučaja.
Prvi je da su oba neg, drugi da su oba poz. Kad su pozitivni onda je x2>=1/x1, pošto je x1>0 (pozitivan) onda je x2 iz <0,1>. Dakle <x1,x2> je <0, +beskonačno>
Drugi slučaj analogno pa se dobije <-beskonačno,0>. U nuli je vrijednost fje 1, to je lok maximum pa je fja konvexna na cijelom R.
Valjda mi je dobra logika....
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:18 sub, 2. 6. 2007 Naslov: Postano: 18:18 sub, 2. 6. 2007 Naslov: |
    |
|
|
Da, imaš pravo...vjerojatno ima neka logika iz one formule, al je derivacijom to najlakše provjerit...
Da, imaš pravo...vjerojatno ima neka logika iz one formule, al je derivacijom to najlakše provjerit...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:51 sub, 2. 6. 2007 Naslov: Postano: 18:51 sub, 2. 6. 2007 Naslov: |
    |
|
|
Btw račun je dobar, samo je obrnuti znak nejednakosti...bar meni....onda bi išla malo drugačija priča...možda i točna...neki zaključci na x1x2<=1, pa pošto x1<x2 iz definicije konvexnosti...možda...
Btw račun je dobar, samo je obrnuti znak nejednakosti...bar meni....onda bi išla malo drugačija priča...možda i točna...neki zaključci na x1x2<=1, pa pošto x1<x2 iz definicije konvexnosti...možda...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 20:01 sub, 2. 6. 2007 Naslov: Postano: 20:01 sub, 2. 6. 2007 Naslov: |
    |
|
|
[quote="Luuka"]Btw račun je dobar, samo je obrnuti znak nejednakosti...bar meni....onda bi išla malo drugačija priča...možda i točna...neki zaključci na x1x2<=1, pa pošto x1<x2 iz definicije konvexnosti...možda...[/quote]
ja sam se u tom računu zapetljao, pa ga neću komentirat. :roll:
ali nešto mi ne štima ipak. uzmi interval <0, 1/2> npr.
:rarrow: tu, po tvojoj nejednakosti, ispada da je funkcija konveksna, a ja sam dobio da je tu konkavna. ak ti se da, probaj 2put derivirat pa vidjet jel moj račun točan. ne kažem da je. ali iz grafa se puno vidi... :prodike:
| Luuka (napisa): | | Btw račun je dobar, samo je obrnuti znak nejednakosti...bar meni....onda bi išla malo drugačija priča...možda i točna...neki zaključci na x1x2⇐1, pa pošto x1<x2 iz definicije konvexnosti...možda... |
ja sam se u tom računu zapetljao, pa ga neću komentirat. 
ali nešto mi ne štima ipak. uzmi interval <0, 1/2> npr.
 tu, po tvojoj nejednakosti, ispada da je funkcija konveksna, a ja sam dobio da je tu konkavna. ak ti se da, probaj 2put derivirat pa vidjet jel moj račun točan. ne kažem da je. ali iz grafa se puno vidi... tu, po tvojoj nejednakosti, ispada da je funkcija konveksna, a ja sam dobio da je tu konkavna. ak ti se da, probaj 2put derivirat pa vidjet jel moj račun točan. ne kažem da je. ali iz grafa se puno vidi... 
_________________
ima let u finish
|
|
| [Vrh] |
|
dvičak
Forumaš(ica)


Pridružen/a: 02. 11. 2006. (17:55:13)
Postovi: (60)16
Spol: 
Lokacija: dj-zg
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
|


















