Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

Pomoć oko integrala (zadatak)
WWW:
Idite na Prethodno  1, 2, 3  Sljedeće
Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
rafaelm
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: muško
Sarma = la pohva - posuda
76 = 86 - 10
Lokacija: Zagreb
PostPostano: 17:16 pet, 8. 6. 2007    Naslov: Citirajte i odgovorite
sin(arccos x)=korjen(1-cos^2(arccos x))=korjen(1-x^2)

ja mislim...

ctg(arccos x)=cos(arccos x)/sin(arccos x)=x/korjen(1-x^2)
sin(arccos x)=korjen(1-cos^2(arccos x))=korjen(1-x^2)

ja mislim...

ctg(arccos x)=cos(arccos x)/sin(arccos x)=x/korjen(1-x^2)



_________________
Rafael Mrđen
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 18:12 pet, 8. 6. 2007    Naslov: Citirajte i odgovorite
@rafaelm Tnx, tak je...

A jel netko riješio 30. za weba a da je dobio onih 200sqrt(2)?? Meni ispada 0, i nikak ne kužim kak bi moglo ispast tolko...
@rafaelm Tnx, tak je...

A jel netko riješio 30. za weba a da je dobio onih 200sqrt(2)?? Meni ispada 0, i nikak ne kužim kak bi moglo ispast tolko...



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 18:31 pet, 8. 6. 2007    Naslov: Citirajte i odgovorite
Zad 30... fulao si ovo:
[latex]\sqrt{x^2} \not= x[/latex] :!:
Vrijedi:
[latex]\sqrt{x^2} = |x|[/latex] ;)

Dakle:
[latex]\int_0^{100\pi} \sqrt2 |\sin x| dx = 100 \int_0^\pi \sqrt2 \sin x dx = -100\sqrt2 \cos x|_0^\pi = 200\sqrt2[/latex]

8)
Zad 30... fulao si ovo:
Exclamation
Vrijedi:
Wink

Dakle:


Cool



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 18:49 pet, 8. 6. 2007    Naslov: Citirajte i odgovorite
ah da :!: :idea:
sad me sram... :oops:
al na greškama se uči, sad znam da je kod određenog integrala modul, a da se ne uzima +...:roll:

hvala vsego... :lol:
ah da Exclamation Idea
sad me sram... Embarassed
al na greškama se uči, sad znam da je kod određenog integrala modul, a da se ne uzima +...Rolling Eyes

hvala vsego... Laughing



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 19:04 pet, 8. 6. 2007    Naslov: Citirajte i odgovorite
Nije to do odredjenog integrala, nego do korijena koji, koristen kao funkcija, uvijek vraca nenegativnu vrijednost, pa ga ne mozes samo "pokratiti" s kvadratom. :)
Nije to do odredjenog integrala, nego do korijena koji, koristen kao funkcija, uvijek vraca nenegativnu vrijednost, pa ga ne mozes samo "pokratiti" s kvadratom. Smile



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
rhiannon
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 06. 2007. (20:34:03)
Postovi: (D)16
Sarma = la pohva - posuda
2 = 2 - 0
PostPostano: 20:49 pon, 11. 6. 2007    Naslov: Citirajte i odgovorite
je li netko može riješiti 39,40 i 31 zadatak
je li netko može riješiti 39,40 i 31 zadatak


[Vrh]
Korisnički profil Pošaljite privatnu poruku
matmih
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: muško
Sarma = la pohva - posuda
36 = 51 - 15
Lokacija: {Zg, De , Ri}
PostPostano: 21:19 pon, 11. 6. 2007    Naslov: Citirajte i odgovorite
31) [latex] \int_{-1}^{1}\frac{dx}{x^2-2xcos\alpha+1} (0<\alpha<\pi)[/latex]
[latex]=\int_{-1}^{1}\frac{dx}{(x-cos\alpha)^2+1-(cos\alpha)^2}=[/latex]
[latex]\int_{-1}^{1}\frac{dx}{(x-cos\alpha)^2+(sin\alpha)^2}=\frac{1}{sin\alpha}arctg\frac{x-cos\alpha}{sin\alpha}\left|\right._{-1}^{1}[/latex]
[latex]=\frac{1}{sin\alpha}[arctg\frac{1-cos\alpha}{sin\alpha}-arctg\frac{-1-cos\alpha}{sin\alpha}][/latex]
[latex]=\frac{1}{sin\alpha}[arctg(tg\frac{\alpha}{2})-arctg(-ctg\frac{\alpha}{2}]=\frac{1}{sin\alpha}[\frac{\alpha}{2}+arctg(tg(\frac{\pi}{2}-\frac{\alpha}{2})][/latex]
[latex]=\frac{1}{sin\alpha}[\frac{\alpha}{2}+\frac{\pi}{2}-\frac{\alpha}{2}]=\frac{1}{sin\alpha}\cdot\frac{\pi}{2}=\frac{\pi}{2sin\alpha} [/latex]

39. i 40. su ogromna gnjavaža sa parcijalnim razlomcima. Tako da ih još nisam rješio. :wink:
31)






39. i 40. su ogromna gnjavaža sa parcijalnim razlomcima. Tako da ih još nisam rješio. Wink




Zadnja promjena: matmih; 21:28 pon, 11. 6. 2007; ukupno mijenjano 1 put.
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
matmih
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: muško
Sarma = la pohva - posuda
36 = 51 - 15
Lokacija: {Zg, De , Ri}
PostPostano: 21:25 pon, 11. 6. 2007    Naslov: Citirajte i odgovorite
Dali zna tko kako dokazati da
[latex] \int_{0}^{+\infty}\frac{dx}{shx}[/latex] divergira :?:
Muče me malo ti nepravi integrali. :oops:
Dali zna tko kako dokazati da
divergira Question
Muče me malo ti nepravi integrali. Embarassed


[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
nana
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: žensko
Sarma = la pohva - posuda
95 = 158 - 63
PostPostano: 21:38 pon, 11. 6. 2007    Naslov: Citirajte i odgovorite
prvo se pravis kao da nemas nepravi integral, dakle trazis primitivnu fju
shx raspisi po definiciji dakle preko e^x

zatim imas suspstituciju t=e^x (ne zaboravi pomaknut rub)

te dobis nepravi integral od 1/(t^2-1)

e sad dolazi u igru limes... treba dalje? ugl trebas dobit da je taj limes inf
prvo se pravis kao da nemas nepravi integral, dakle trazis primitivnu fju
shx raspisi po definiciji dakle preko e^x

zatim imas suspstituciju t=e^x (ne zaboravi pomaknut rub)

te dobis nepravi integral od 1/(t^2-1)

e sad dolazi u igru limes... treba dalje? ugl trebas dobit da je taj limes inf



_________________
Kad sam bila mala htjela sam biti statističarka Very Happy
[tex]\omega \in \Omega[/tex] Srce
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
matmih
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: muško
Sarma = la pohva - posuda
36 = 51 - 15
Lokacija: {Zg, De , Ri}
PostPostano: 22:03 pon, 11. 6. 2007    Naslov: Citirajte i odgovorite
Hvala kolegice, mislim da ću znat dalje... :D
Hvala kolegice, mislim da ću znat dalje... Very Happy


[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 17:29 uto, 12. 6. 2007    Naslov: Citirajte i odgovorite
Može li se 50.zad riješit onak rekurzivno, kao što je matmih riješio ranije na ovom topicu u sklopu neodređenog integrala
x^2 dx / (x^2+1)^2 ? U raspisu toga se pojavljuje int dx/(1+x^2)^2 a baš taj je u ovom nepravom obliku...

Ta rekurzivna ideja je jedina za taj zadatak...traže se nove ili modifikacija iste...
Može li se 50.zad riješit onak rekurzivno, kao što je matmih riješio ranije na ovom topicu u sklopu neodređenog integrala
x^2 dx / (x^2+1)^2 ? U raspisu toga se pojavljuje int dx/(1+x^2)^2 a baš taj je u ovom nepravom obliku...

Ta rekurzivna ideja je jedina za taj zadatak...traže se nove ili modifikacija iste...



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
matmih
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: muško
Sarma = la pohva - posuda
36 = 51 - 15
Lokacija: {Zg, De , Ri}
PostPostano: 18:33 uto, 12. 6. 2007    Naslov: Citirajte i odgovorite
Ono rekurzivno je bilo baš za [latex] \int\frac{dx}{(1+x^2)^2}[/latex] kada uzmemo n=1. Uzmeš za primitivnu funkciju ono šta se dobije i samo dodaš granice integracije.
Znači: [latex] \lim_{r\to+\infty}(\frac{1}{2}\cdot(arctgx+\frac{x}{1+x^2})\left|\right._{0}^{r})=\frac{1}{2}\frac{\pi}{2}=\frac{\pi}{4}[/latex]. Mislim da je to jedini način. Ako neko zna drugi neka napiše.
Ono rekurzivno je bilo baš za kada uzmemo n=1. Uzmeš za primitivnu funkciju ono šta se dobije i samo dodaš granice integracije.
Znači: . Mislim da je to jedini način. Ako neko zna drugi neka napiše.


[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
Mr.Doe
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
Sarma = la pohva - posuda
20 = 50 - 30
PostPostano: 10:03 sri, 13. 6. 2007    Naslov: Citirajte i odgovorite
Ima.

[latex]\displaystlyle \int_{0}^{\infty}\frac{dx}{(x^2+1)^2}=\{t=x^2+1, dx=\frac{1}{2}(t-1)^{-1/2}dt \}=[/latex]
[latex]\int_{1}^{\infty}\frac{1 t^{-2}}{2}(t-1)^{-1/2}dt=\{ t=\frac{1}{u} ,dt=\frac{-1}{u^2}du \} =[/latex]
[latex]\frac{1}{2}\int_{0}^{1} u^2(\frac{1}{u}-1)^{-1/2}\frac{1}{u^2}du=
\frac{1}{2}\int_{0}^{1}(\frac{1}{u}-1)^{-1/2}du=[/latex]
[latex]
\frac{1}{2}\int_{0}^{1}(1-u)^{-1/2}u^{1/2}du=
\frac{1}{2}\int_{0}^{1} (1-u)^{1/2-1}u^{3/2-1}du=[/latex]
[latex]\frac{1}{2}B(\frac{3}{2},\frac{1}{2})=
\frac{1}{2}\frac{\Gamma (\frac{3}{2})\Gamma(\frac{1}{2})}{\Gamma(2)}=
\frac{1}{4} (\Gamma(\frac{1}{2}))^2[/latex] , a ovog zadnjeg se najvjerojatnije sjecate sa UVISA, i [latex]\displaystyle=\frac{\pi}{4}[/latex]

Ako sam negdje pogrjesio sam recite.

(znam da sam ponovno preskocio puno stvari,no mislim da to ne bi trebao biti problem za vas 8) )
Ima.





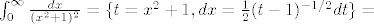
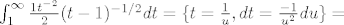
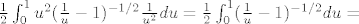
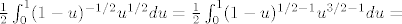
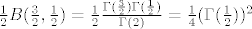, a ovog zadnjeg se najvjerojatnije sjecate sa UVISA, i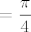

Ako sam negdje pogrjesio sam recite.

(znam da sam ponovno preskocio puno stvari,no mislim da to ne bi trebao biti problem za vas Cool )


[Vrh]
Korisnički profil Pošaljite privatnu poruku
nana
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: žensko
Sarma = la pohva - posuda
95 = 158 - 63
PostPostano: 10:53 čet, 14. 6. 2007    Naslov: Citirajte i odgovorite
@Mr.Doe : UVIS tj UV i US su na 2. tj 3. godini.

postoji jos jedan nacin:

[latex]\int_{0}^{\infty}\frac{dx}{(x^2+1)^2} =...[/latex]


[latex]\frac{1}{(x^2+1)^2}=\frac{x^2+1-x^2}{(x^2+1)^2}=\frac{1}{x^2+1} -\frac{x^2}{(x^2+1)^2}=\frac{1}{(x^2+1)} - x*\frac{x}{(x^2+1)^2} [/latex]

[latex] du=\frac{x}{(x^2+1)^2} [/latex]


[latex] v=x[/latex]
@Mr.Doe : UVIS tj UV i US su na 2. tj 3. godini.

postoji jos jedan nacin:












_________________
Kad sam bila mala htjela sam biti statističarka Very Happy
[tex]\omega \in \Omega[/tex] Srce
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 16:30 čet, 14. 6. 2007    Naslov: Citirajte i odgovorite
Hvala nana, tak nešto sam tražio :idea: !!!
To je ta mala ideja koja čini ovaj svijet ljepšim mjestom za život...hehe
Hvala nana, tak nešto sam tražio Idea !!!
To je ta mala ideja koja čini ovaj svijet ljepšim mjestom za život...hehe



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
ivanzub
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
Sarma = la pohva - posuda
3 = 6 - 3
PostPostano: 11:22 ned, 17. 6. 2007    Naslov: Citirajte i odgovorite
moze mala pomoc za 17. zadatak: integral (x^5)e^x^3dx ?
nikako mi ne ispada dobro! :(
moze mala pomoc za 17. zadatak: integral (x^5)e^x^3dx ?
nikako mi ne ispada dobro! Sad


[Vrh]
Korisnički profil Pošaljite privatnu poruku
dvičak
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 02. 11. 2006. (17:55:13)
Postovi: (60)16
Spol: muško
Sarma = la pohva - posuda
18 = 19 - 1
Lokacija: dj-zg
PostPostano: 12:04 ned, 17. 6. 2007    Naslov: Citirajte i odgovorite
napraviš supstituciju t= x^3, pa dobiješ 1/3 t e^t dt , dalje parc. integracijom
napraviš supstituciju t= x^3, pa dobiješ 1/3 t e^t dt , dalje parc. integracijom



_________________
potpis
[Vrh]
Korisnički profil Pošaljite privatnu poruku
napraviculom
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: muško
Sarma = la pohva - posuda
14 = 16 - 2
Lokacija: Scranton
PostPostano: 9:13 sri, 20. 6. 2007    Naslov: Citirajte i odgovorite
moze netko dat ideju za:
int 1/(x * (lnx)^4/3) dx
(to je nepravi integral iz kolokvija od prosle godine)
granice: 0,1/3

editirano(nisam siguran sta sam prije napisao)
moze netko dat ideju za:
int 1/(x * (lnx)^4/3) dx
(to je nepravi integral iz kolokvija od prosle godine)
granice: 0,1/3

editirano(nisam siguran sta sam prije napisao)




Zadnja promjena: napraviculom; 9:47 sri, 20. 6. 2007; ukupno mijenjano 5 put/a.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
dvičak
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 02. 11. 2006. (17:55:13)
Postovi: (60)16
Spol: muško
Sarma = la pohva - posuda
18 = 19 - 1
Lokacija: dj-zg
PostPostano: 9:19 sri, 20. 6. 2007    Naslov: Citirajte i odgovorite
uzmi supstituciju x=2sint
uzmi supstituciju x=2sint



_________________
potpis
[Vrh]
Korisnički profil Pošaljite privatnu poruku
napraviculom
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: muško
Sarma = la pohva - posuda
14 = 16 - 2
Lokacija: Scranton
PostPostano: 10:29 sri, 20. 6. 2007    Naslov: Citirajte i odgovorite
hvala, ali dao si uputu za zadatak koji sam slucajno prije copy/paste-ao. Ovaj me zanima
int 1/(x * (lnx)^4/3) dx granice: 0,1/3
hvala, ali dao si uputu za zadatak koji sam slucajno prije copy/paste-ao. Ovaj me zanima
int 1/(x * (lnx)^4/3) dx granice: 0,1/3


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2 Vremenska zona: GMT + 01:00.
Idite na Prethodno  1, 2, 3  Sljedeće
Stranica 2 / 3.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan