| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
shimija
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
 Postano: 17:10 ned, 24. 6. 2007 Naslov: Postano: 17:10 ned, 24. 6. 2007 Naslov: |
    |
|
|
[quote="herman"]Još jedno pitanje iz kolokvija 10.6.2005(http://web.math.hr/nastava/la/kolokviji/04-05/la2/kol2a.pdf) - dal je neko rješavao 3. zadatak, i kolko mu je ispalo? Riješih ga, ali iz nepoznatog razloga imam osjećaj da je krivo...Ispao mi opći član niza [latex]a_{n} = \frac{2\cdot 9^n}{4^n}[/latex]. Hvala unaprijed! :wink:[/quote]
evo san ga ja riješia i ispa mi je [latex]a_{n}=\frac{9^{n-1}+2\cdot4^{n-1}}{2\cdot9^{n-1}-4^{n-1}}[/latex] ,
al dug je postupak pa nije čudno ako se falije, samo da se ne desi u kolokviju... :wink:
| herman (napisa): | Još jedno pitanje iz kolokvija 10.6.2005(http://web.math.hr/nastava/la/kolokviji/04-05/la2/kol2a.pdf) - dal je neko rješavao 3. zadatak, i kolko mu je ispalo? Riješih ga, ali iz nepoznatog razloga imam osjećaj da je krivo...Ispao mi opći član niza 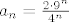 . Hvala unaprijed! . Hvala unaprijed!  |
evo san ga ja riješia i ispa mi je 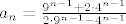 , ,
al dug je postupak pa nije čudno ako se falije, samo da se ne desi u kolokviju... 
Zadnja promjena: shimija; 2:33 pon, 25. 6. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
 Postano: 18:05 ned, 24. 6. 2007 Naslov: Postano: 18:05 ned, 24. 6. 2007 Naslov: |
    |
|
|
moze pitanje? ovak, zadaci tipa odredite ONB u kojoj se matrica A dijagonalizira?
e sad, prvo izracunam svojstvene vektore potprostora. dobijem neki skup {v1,v2,v3},koji razapinju potprostore tih nekih odredenih sv.vrijednosti.
sad moram provjerit da li su ti vektori okomiti tj gledam
(v1|v2)=0,
(v1|v3)=0,
(v1|v2)=0,
ukoliko neki od ovih kombinacija ispadne 0 npr. da to bude skup {v1,v3} tada moram taj skup ortonormirat(GS) i jos na kraju ovog treceg, u ovom slucaju v2 samo normirat. i tada je taj novonastali skup {v1',v2',v3'} ONB baza u kojoj se A dijagonalizira?
da li to ide tak ili sam negdje nesto fulao? 8)
moze pitanje? ovak, zadaci tipa odredite ONB u kojoj se matrica A dijagonalizira?
e sad, prvo izracunam svojstvene vektore potprostora. dobijem neki skup {v1,v2,v3},koji razapinju potprostore tih nekih odredenih sv.vrijednosti.
sad moram provjerit da li su ti vektori okomiti tj gledam
(v1|v2)=0,
(v1|v3)=0,
(v1|v2)=0,
ukoliko neki od ovih kombinacija ispadne 0 npr. da to bude skup {v1,v3} tada moram taj skup ortonormirat(GS) i jos na kraju ovog treceg, u ovom slucaju v2 samo normirat. i tada je taj novonastali skup {v1',v2',v3'} ONB baza u kojoj se A dijagonalizira?
da li to ide tak ili sam negdje nesto fulao? 
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 18:38 ned, 24. 6. 2007 Naslov: Postano: 18:38 ned, 24. 6. 2007 Naslov: |
    |
|
|
[quote="shimija"][quote="herman"]Još jedno pitanje iz kolokvija 10.6.2005(http://web.math.hr/nastava/la/kolokviji/04-05/la2/kol2a.pdf) - dal je neko rješavao 3. zadatak, i kolko mu je ispalo? Riješih ga, ali iz nepoznatog razloga imam osjećaj da je krivo...Ispao mi opći član niza [latex]a_{n} = \frac{2\cdot 9^n}{4^n}[/latex]. Hvala unaprijed! :wink:[/quote]
evo san ga ja riješia i ispa mi je [latex]a_{n}=\frac{9^{n-1}+2\cdot4^{n-1}}{2\cdot9^{n-1}-4^n}[/latex] ,
al dug je postupak pa nije čudno ako se falije, samo da se ne desi u kolokviju... :wink:[/quote]
Ovo mi se čini točno, ajd please napiši ukratko postupak.
| shimija (napisa): | | herman (napisa): | Još jedno pitanje iz kolokvija 10.6.2005(http://web.math.hr/nastava/la/kolokviji/04-05/la2/kol2a.pdf) - dal je neko rješavao 3. zadatak, i kolko mu je ispalo? Riješih ga, ali iz nepoznatog razloga imam osjećaj da je krivo...Ispao mi opći član niza 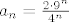 . Hvala unaprijed! . Hvala unaprijed!  |
evo san ga ja riješia i ispa mi je 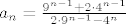 , ,
al dug je postupak pa nije čudno ako se falije, samo da se ne desi u kolokviju...  |
Ovo mi se čini točno, ajd please napiši ukratko postupak.
|
|
| [Vrh] |
|
shimija
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
|
| [Vrh] |
|
shimija
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
shimija
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 11:07 pon, 25. 6. 2007 Naslov: Postano: 11:07 pon, 25. 6. 2007 Naslov: |
    |
|
|
@ivanzub Mislim da si fulao. Jer ako ispadne da je (v1|v3)=0 onda su ti vektori okomiti (ortogonalni) i onda njih trebaš normirat, a za v2 napravit GS. Nek me netko ispravi ak krivo mislim...
@ivanzub Mislim da si fulao. Jer ako ispadne da je (v1|v3)=0 onda su ti vektori okomiti (ortogonalni) i onda njih trebaš normirat, a za v2 napravit GS. Nek me netko ispravi ak krivo mislim...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 11:22 pon, 25. 6. 2007 Naslov: Postano: 11:22 pon, 25. 6. 2007 Naslov: |
    |
|
|
evo. sad pogledah. ovako: da bi se matrica operatora u nekoj onb mogla dijagonalizirati, taj operator mora biti normalan, tj. mora vrijediti A*A=AA* (odnosno njegov matrični zapis mora biti normalan). znači prvo to provjeriš. ako ne vrijedi ne moraš ni pokušavati. inače, nađeš svojstvene potprostore. vektori iz različitih svojstvenih potprostora su međusobno okomiti (što je vjerojatno posljedica normalnosti operatora :? - neka netko potvrdi ako zna), ali vektori baze istog svojstvenog potprostora ne moraju biti ortonormirani. u tom ih slučaju gspiraš, a ove ostale samo normiraš (ako treba).
čestitam, dobili ste ortonormiranu bazu u kojoj se dana matrica dijagonalizira. 8)
:pile:
evo. sad pogledah. ovako: da bi se matrica operatora u nekoj onb mogla dijagonalizirati, taj operator mora biti normalan, tj. mora vrijediti A*A=AA* (odnosno njegov matrični zapis mora biti normalan). znači prvo to provjeriš. ako ne vrijedi ne moraš ni pokušavati. inače, nađeš svojstvene potprostore. vektori iz različitih svojstvenih potprostora su međusobno okomiti (što je vjerojatno posljedica normalnosti operatora  - neka netko potvrdi ako zna), ali vektori baze istog svojstvenog potprostora ne moraju biti ortonormirani. u tom ih slučaju gspiraš, a ove ostale samo normiraš (ako treba). - neka netko potvrdi ako zna), ali vektori baze istog svojstvenog potprostora ne moraju biti ortonormirani. u tom ih slučaju gspiraš, a ove ostale samo normiraš (ako treba).
čestitam, dobili ste ortonormiranu bazu u kojoj se dana matrica dijagonalizira. 

_________________
ima let u finish
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
|

















