| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
amihic
Forumaš(ica)

Pridružen/a: 12. 06. 2005. (14:05:58)
Postovi: (24)16
|
 Postano: 23:38 sri, 20. 6. 2007 Naslov: razni dokazi Postano: 23:38 sri, 20. 6. 2007 Naslov: razni dokazi |
    |
|
|
imam nekoliko pitanja..
1.kada funkciju f:D(podskup od Rn)->R prosirimo na citav Rn(tada se funkcija zove f*.teotem kaze:f konveksna akko f* konveksna.kako to dokazati??
2.Lema:neka x iz Cl C,x* iz ri C.Tada je poluotvoreni segment<x,x*] cijeli sadrzan u ri C.
pitanja:prvo,meni ovdje ne pise da je C konveksan.Da li je to jedan od preduvjeta tvrdnje?
postoje posljedice ove leme; 1)da je ri C konveksan
2)skupovi C,ri C i Cl C imaju isti relativni interior,zatvarac i granicu
Kako dokazati te dvije tvrdnje?
3.Dokaz jedinstvenosti projekcije od x na C???
4.propozicija:x"=Pk(x) (x" je projekcija od x na k-zatvoren konveksan konus) akko x" iz K,x-x" iz K*,<x-x",x">=o
<= smjer ne razumijem
5.propozicija:Tangencijalni konus je zatvoren
Imam jako lose fotokopije pa bi bilo odlicno da netko napise cijeli dokaz
Unaprijed hvala na odgovorima!!
imam nekoliko pitanja..
1.kada funkciju f (podskup od Rn)->R prosirimo na citav Rn(tada se funkcija zove f*.teotem kaze:f konveksna akko f* konveksna.kako to dokazati?? (podskup od Rn)->R prosirimo na citav Rn(tada se funkcija zove f*.teotem kaze:f konveksna akko f* konveksna.kako to dokazati??
2.Lema:neka x iz Cl C,x* iz ri C.Tada je poluotvoreni segment<x,x*] cijeli sadrzan u ri C.
pitanja:prvo,meni ovdje ne pise da je C konveksan.Da li je to jedan od preduvjeta tvrdnje?
postoje posljedice ove leme; 1)da je ri C konveksan
2)skupovi C,ri C i Cl C imaju isti relativni interior,zatvarac i granicu
Kako dokazati te dvije tvrdnje?
3.Dokaz jedinstvenosti projekcije od x na C???
4.propozicija:x"=Pk(x) (x" je projekcija od x na k-zatvoren konveksan konus) akko x" iz K,x-x" iz K*,<x-x",x">=o
<= smjer ne razumijem
5.propozicija:Tangencijalni konus je zatvoren
Imam jako lose fotokopije pa bi bilo odlicno da netko napise cijeli dokaz
Unaprijed hvala na odgovorima!!
_________________
ana
|
|
| [Vrh] |
|
markov
Forumaš(ica)

Pridružen/a: 04. 01. 2006. (01:24:33)
Postovi: (121)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
 Postano: 18:13 uto, 26. 6. 2007 Naslov: Postano: 18:13 uto, 26. 6. 2007 Naslov: |
    |
|
|
[quote="Anonymous"]Kako se pokaze f sublinearna <= njen epigraf neprazan konveksan konus?
i moze li netko napisati dokaz tm-a o Lipschitzavosti?
hvala![/quote]
Treba pokazati: epi f konus => f je poz.hom.st 1
(x, f(x)) je iz epi f, pa je t (x, f(x)) iz efi f, pa je tf(x) >= f (tx), sto je ekvivalentno tome da je f poz.hom.st 1
| Anonymous (napisa): | Kako se pokaze f sublinearna ⇐ njen epigraf neprazan konveksan konus?
i moze li netko napisati dokaz tm-a o Lipschitzavosti?
hvala! |
Treba pokazati: epi f konus ⇒ f je poz.hom.st 1
(x, f(x)) je iz epi f, pa je t (x, f(x)) iz efi f, pa je tf(x) >= f (tx), sto je ekvivalentno tome da je f poz.hom.st 1
|
|
| [Vrh] |
|
Gost
|
 Postano: 17:46 sri, 27. 6. 2007 Naslov: Re: razni dokazi Postano: 17:46 sri, 27. 6. 2007 Naslov: Re: razni dokazi |
    |
|
|
[quote="amihic"]
3.Dokaz jedinstvenosti projekcije od x na C???
[/quote]
Neka su x1 i x2 projekcije od x. Spoji x, x1, x2 u trokut. Povuci visinu na stranicu x1 i x2, ona je kraca od obje hipotenuze, pa je i projekcija po toj visini kraca od obje hipotenuze, sto je kontradicija s time da su x1, x2 tocke skupa C najblize tocki x, nasli smo jednu bližu.
| amihic (napisa): |
3.Dokaz jedinstvenosti projekcije od x na C???
|
Neka su x1 i x2 projekcije od x. Spoji x, x1, x2 u trokut. Povuci visinu na stranicu x1 i x2, ona je kraca od obje hipotenuze, pa je i projekcija po toj visini kraca od obje hipotenuze, sto je kontradicija s time da su x1, x2 tocke skupa C najblize tocki x, nasli smo jednu bližu.
|
|
| [Vrh] |
|
Gost
|
 Postano: 21:10 sri, 27. 6. 2007 Naslov: Postano: 21:10 sri, 27. 6. 2007 Naslov: |
    |
|
|
Kod dokaza teorema: Ako C nije prazan skup => riC nije prazan skup i dim(riC)=dim C, kako dokazemo specijalan slucaj, tj.kad pretpostavimo da je C=conv{x1,...xk}, gdje su x1,...xk u opcem polozaju?
Kod dokaza teorema: Ako C nije prazan skup => riC nije prazan skup i dim(riC)=dim C, kako dokazemo specijalan slucaj, tj.kad pretpostavimo da je C=conv{x1,...xk}, gdje su x1,...xk u opcem polozaju?
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 17:00 čet, 5. 7. 2007 Naslov: Postano: 17:00 čet, 5. 7. 2007 Naslov: |
    |
|
|
Da aktualiziram :
[latex]\overline{x}[/latex] je projekcija od [latex]x[/latex] na [latex]C[/latex] akko [latex]\overline{x}\in C , x-\overline{x}\in C^* , <x-\overline{x},\overline{x}>=0[/latex].
Nije mi uopce jasno kako smo dobili [latex]<x-\overline{x},\overline{x}>=0[/latex] . Mi smo koristili [latex]<x-\overline{x},y-\overline{x}>\leq 0,\forall y\in C[/latex], zatim smo uzeli [latex]y:=\alpha \overline{x},\alpha \geq 0[/latex], i onda dokazivali trazenu jednakost. No , mi ne mozemo tvrditi da [latex]\alpha x\in C, \alpha \geq 0 [/latex], to bi vrijedilo kada bi [latex]C[/latex] bio konus no mi to ne mozemo pretpostaviti , te znamo jedino za [latex]\alpha=1,\alpha x\in C[/latex]. Uzemo kontraprimjer, npr jedinicni krug sa sredistem u [latex](1,1)[/latex], i projeciramo [latex]x=(1,-1)[/latex] , projekcija na [latex] C[/latex] je [latex](1,0)[/latex] , no [latex]\alpha x \notin C , \alpha \geq 0, \alpha \neq 1[/latex]. Pomozite!
Da aktualiziram :
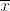 je projekcija od je projekcija od  na na  akko akko 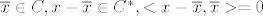 . .
Nije mi uopce jasno kako smo dobili 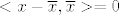 . Mi smo koristili . Mi smo koristili 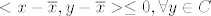 , zatim smo uzeli , zatim smo uzeli 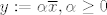 , i onda dokazivali trazenu jednakost. No , mi ne mozemo tvrditi da , i onda dokazivali trazenu jednakost. No , mi ne mozemo tvrditi da 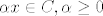 , to bi vrijedilo kada bi , to bi vrijedilo kada bi  bio konus no mi to ne mozemo pretpostaviti , te znamo jedino za bio konus no mi to ne mozemo pretpostaviti , te znamo jedino za 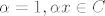 . Uzemo kontraprimjer, npr jedinicni krug sa sredistem u . Uzemo kontraprimjer, npr jedinicni krug sa sredistem u 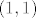 , i projeciramo , i projeciramo 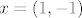 , projekcija na , projekcija na 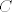 je je 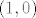 , no , no 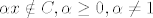 . Pomozite! . Pomozite!
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|





