| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
shoki
Forumaš(ica)

Pridružen/a: 06. 04. 2004. (13:05:09)
Postovi: (50)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:32 sri, 11. 7. 2007 Naslov: Postano: 22:32 sri, 11. 7. 2007 Naslov: |
    |
|
|
Sutra počinje u 8.30 u 108...al ima više grupa, najviše ljudi je u 12.30...
Sutra počinje u 8.30 u 108...al ima više grupa, najviše ljudi je u 12.30...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Nori
Forumaš(ica)
Pridružen/a: 01. 10. 2006. (18:41:07)
Postovi: (E5)16
Spol: 
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
Nori
Forumaš(ica)
Pridružen/a: 01. 10. 2006. (18:41:07)
Postovi: (E5)16
Spol: 
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
shoki
Forumaš(ica)

Pridružen/a: 06. 04. 2004. (13:05:09)
Postovi: (50)16
|
 Postano: 9:23 čet, 12. 7. 2007 Naslov: Postano: 9:23 čet, 12. 7. 2007 Naslov: |
    |
|
|
[quote="sunny"]A zasto shoki ne bi jednostavno dosao danas prvo na pismeni dio usmenog (18:30) pa onda sutra na usmeni dio usmenog!? Mislim da samo na usmeni dio nema svrhe dolaziti osim ako Shoki nema neki dobar izgovor zasto ne moze na pismeni dio izaci. A koliko sam skuzila (po sinocnjem stanju) prof. bi ga trebao pusititi da danas pise pismeni dio unatoc tome sto nije upisan na onaj popis, al' Shoki nemoj me drzat za rijec. Ajd drzim ti fige da uspijes!!
...i sretno svima danas!!!!!!!![/quote]
hvala, hvala, hvala, imaš cugu od mene, hvala bogu netko sa konkretnom informacijom....
šteta što nema adekvatnog smajlića da te njime zaspamam...
hvala još jednom
| sunny (napisa): | A zasto shoki ne bi jednostavno dosao danas prvo na pismeni dio usmenog (18:30) pa onda sutra na usmeni dio usmenog!? Mislim da samo na usmeni dio nema svrhe dolaziti osim ako Shoki nema neki dobar izgovor zasto ne moze na pismeni dio izaci. A koliko sam skuzila (po sinocnjem stanju) prof. bi ga trebao pusititi da danas pise pismeni dio unatoc tome sto nije upisan na onaj popis, al' Shoki nemoj me drzat za rijec. Ajd drzim ti fige da uspijes!!
...i sretno svima danas!!!!!!!! |
hvala, hvala, hvala, imaš cugu od mene, hvala bogu netko sa konkretnom informacijom....
šteta što nema adekvatnog smajlića da te njime zaspamam...
hvala još jednom
|
|
| [Vrh] |
|
shoki
Forumaš(ica)

Pridružen/a: 06. 04. 2004. (13:05:09)
Postovi: (50)16
|
|
| [Vrh] |
|
the maja
Forumaš(ica)

Pridružen/a: 26. 11. 2006. (09:35:27)
Postovi: (5D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
shoki
Forumaš(ica)

Pridružen/a: 06. 04. 2004. (13:05:09)
Postovi: (50)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
dosed_girl
Forumaš(ica)

Pridružen/a: 04. 12. 2006. (21:01:46)
Postovi: (6F)16
Spol: 
Lokacija: -zG-
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
the maja
Forumaš(ica)

Pridružen/a: 26. 11. 2006. (09:35:27)
Postovi: (5D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 9:09 pet, 13. 7. 2007 Naslov: Postano: 9:09 pet, 13. 7. 2007 Naslov: |
    |
|
|
[quote="the maja"]trebam pomoć...
kako bi dokazali da je red (-1)1/n=ln2...trebamo tu kao koristiti abelov teorem i svašta nešto, a meni to stvarno nije jasno pa pomagajte...
i da, sorrite na ružnom zapisu :)[/quote]
Pogledaj Taylorov red oko 0 za funkciju [latex]f :t \mapsto \frac{1}{1+t}[/latex] (geom. red)
[latex]f(t)=\frac{1}{1+t}=\sum_{n=0}^\infty (-1)^{n}t^n.[/latex]
Njegov radijus konvergencije je [latex]1[/latex].
Budući da se redovi potencija mogu integrirati član po član na području konvergencije (tj. tako dobiveni red će konvergirati prema odgovarajućoj primitivnoj funkciji od [latex]f[/latex]), za [latex]x \in \langle -1,1 \rangle [/latex] imamo
[latex]\ln(1+x)=\int_{0}^x\frac{1}{1+t} dt=\sum_{n=0}^\infty [(-1)^{n} \int_0 ^x t^n dx]= [/latex][latex]\sum_{n=0}^\infty (-1)^{n}\frac{x^{n+1}}{n+1}= \sum_{n=1}^\infty (-1)^{n-1}\frac{x^n}{n}[/latex].
Također znamo da je radijus konvergencije gornjeg reda jednak 1, jer se radijus konvergencije reda potencija ne mijenja pri deriviranju/integriranju član po član.
No gornji red prema Leibnizovom kriteriju konvergira i u točki [latex] x=1 [/latex] (riječ je o redu [latex]\sum_{n=1}^\infty (-1)^{n-1}\frac{1}{n}[/latex], a to je alternirajuć red, čiji članovi strogo padaju i teže prema 0).
Stoga je sa [latex]g : x \mapsto\sum_{n=1}^\infty (-1)^{n-1}\frac{x^n}{n} [/latex] dobro definirana funkcija na [latex]\langle -1,1][/latex], koja se na [latex]\langle -1, 1\rangle [/latex] podudara sa funkcijom [latex] x \mapsto \ln(1+x)[/latex].
I sada možeš iskoristiti (drugi) Abelov teorem, koji u ovom slučaju kaže da je funkcija [latex]g : x \mapsto \sum_{n=1}^\infty (-1)^{n-1}\frac{x^n}{n}[/latex] neprekidna slijeva u točki 1.
Dakle,
[latex]\sum_{n=1}^\infty (-1)^{n-1}\frac{1}{n}=g(1)=\lim_ {x \rightarrow 1^-}g(x)=[/latex][latex] \lim_ {x \rightarrow 1^-}\sum_{n=1}^\infty (-1)^{n-1}\frac{x^n}{n}=\lim_{x \rightarrow 1^-}\ln(1+x)=\ln2[/latex].
| the maja (napisa): | trebam pomoć...
kako bi dokazali da je red (-1)1/n=ln2...trebamo tu kao koristiti abelov teorem i svašta nešto, a meni to stvarno nije jasno pa pomagajte...
i da, sorrite na ružnom zapisu  |
Pogledaj Taylorov red oko 0 za funkciju 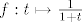 (geom. red) (geom. red)
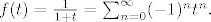
Njegov radijus konvergencije je  . .
Budući da se redovi potencija mogu integrirati član po član na području konvergencije (tj. tako dobiveni red će konvergirati prema odgovarajućoj primitivnoj funkciji od  ), za ), za 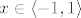 imamo imamo
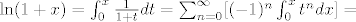 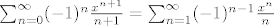 . .
Također znamo da je radijus konvergencije gornjeg reda jednak 1, jer se radijus konvergencije reda potencija ne mijenja pri deriviranju/integriranju član po član.
No gornji red prema Leibnizovom kriteriju konvergira i u točki  (riječ je o redu (riječ je o redu 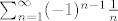 , a to je alternirajuć red, čiji članovi strogo padaju i teže prema 0). , a to je alternirajuć red, čiji članovi strogo padaju i teže prema 0).
Stoga je sa 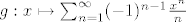 dobro definirana funkcija na dobro definirana funkcija na 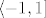 , koja se na , koja se na 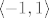 podudara sa funkcijom podudara sa funkcijom 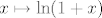 . .
I sada možeš iskoristiti (drugi) Abelov teorem, koji u ovom slučaju kaže da je funkcija 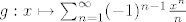 neprekidna slijeva u točki 1. neprekidna slijeva u točki 1.
Dakle,
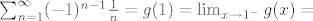 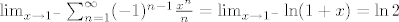 . .
|
|
| [Vrh] |
|
fireball
Forumaš(ica)


Pridružen/a: 07. 10. 2005. (18:49:17)
Postovi: (4AB)16
Spol: 
Lokacija: s rukom u vatri i nogom u grobu
|
|
| [Vrh] |
|
Chvarak
Forumaš(ica)


Pridružen/a: 06. 12. 2006. (14:12:04)
Postovi: (12)16
Spol: 
|
|
| [Vrh] |
|
|
















