| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 15:03 uto, 18. 9. 2007 Naslov: Postano: 15:03 uto, 18. 9. 2007 Naslov: |
    |
|
|
[quote="LSSD"]
Znam da je zbroj dvije nezavisne binomne binomna, ali me zanima kako ide ova obratna konstrukcija:)[/quote]
To ti je to jer ako [latex]n\geq 2[/latex] uvijek mozes uzeti [latex]m_1=1[/latex] i [latex]m_2=n-1[/latex], no puno zanimljivije jest to sto je asistent stavio [latex]n\in\mathbb{N}[/latex], pa ne znam sta bi napravili ako [latex]n=1[/latex]. Sta da uzmemo [latex]m_1=1,m_2=0[/latex], no kakva bi to bila binomna sa parametrima [latex]B(0,p)[/latex]?
Edit: imas pravo Gauss.
| LSSD (napisa): |
Znam da je zbroj dvije nezavisne binomne binomna, ali me zanima kako ide ova obratna konstrukcija:) |
To ti je to jer ako 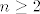 uvijek mozes uzeti uvijek mozes uzeti 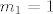 i i 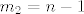 , no puno zanimljivije jest to sto je asistent stavio , no puno zanimljivije jest to sto je asistent stavio 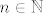 , pa ne znam sta bi napravili ako , pa ne znam sta bi napravili ako 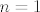 . Sta da uzmemo . Sta da uzmemo 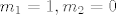 , no kakva bi to bila binomna sa parametrima , no kakva bi to bila binomna sa parametrima 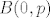 ? ?
Edit: imas pravo Gauss.
Zadnja promjena: Mr.Doe; 15:22 uto, 18. 9. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 15:09 uto, 18. 9. 2007 Naslov: Postano: 15:09 uto, 18. 9. 2007 Naslov: |
    |
|
|
[quote="Mr.Doe"][quote="LSSD"]
Znam da je zbroj dvije nezavisne binomne binomna, ali me zanima kako ide ova obratna konstrukcija:)[/quote]
To ti je to jer ako [latex]n\geq 2[/latex] uvijek mozes uzeti [latex]m_1=1[/latex] i [latex]m_2=n-1[/latex], no puno zanimljivije jest to sto je asistent stavio [latex]n\in\mathbb{N}[/latex], pa ne znam sta bi napravili ako [latex]n=1[/latex]. Sta da uzmemo [latex]m_1=1,m_2=0[/latex], no kakva bi to bila binomna sa parametrima [latex]B(0,p)[/latex]?[/quote]
ti ovdje nisi pokazao da su X i Y binomne vec samo da postoje F~B(m1,p) i G~B(m2,p) t.d. je F+G~B(n,p)~X+Y.
a za ovo s n<=2 nije ni meni jasno
| Mr.Doe (napisa): | | LSSD (napisa): |
Znam da je zbroj dvije nezavisne binomne binomna, ali me zanima kako ide ova obratna konstrukcija:) |
To ti je to jer ako 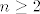 uvijek mozes uzeti uvijek mozes uzeti 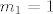 i i 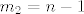 , no puno zanimljivije jest to sto je asistent stavio , no puno zanimljivije jest to sto je asistent stavio 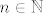 , pa ne znam sta bi napravili ako , pa ne znam sta bi napravili ako 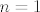 . Sta da uzmemo . Sta da uzmemo 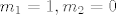 , no kakva bi to bila binomna sa parametrima , no kakva bi to bila binomna sa parametrima 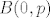 ? ? |
ti ovdje nisi pokazao da su X i Y binomne vec samo da postoje F~B(m1,p) i G~B(m2,p) t.d. je F+G~B(n,p)~X+Y.
a za ovo s n⇐2 nije ni meni jasno
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 15:21 uto, 18. 9. 2007 Naslov: Postano: 15:21 uto, 18. 9. 2007 Naslov: |
    |
|
|
[quote="LSSD"]Znas li rijesenje slijedeceg:
Neka su X i Y nezavisne cjelobrojne nenegativne slucajne varijable takve da je X+Y binomna sa parametrima (n,p). Dokazite da postoje m1,m2 takvi da je m1+m2=n, X je binomna s parametrima (m1,p), a Y binomna s parametrima (m2,p).
Znam da je zbroj dvije nezavisne binomne binomna, ali me zanima kako ide ova obratna konstrukcija:)[/quote]
Počneš od X~B(m1,p), Y~B(m2,p). Tada X+Y prima vrijednosti od 0 do m1+m2.
Sada je neki [latex]k \in \{0,1,\dots,m_1+m_2\}[/latex],
pa je
[latex]P(X+Y=k)=P(X+Y=k, \cup_{l=0}^{m_1}\{X=l\})=\sum_{l=0}^{m_1}P(X+Y=k,X=l)=[/latex]
[latex]\sum_{l=0}^{m_1}P(Y=k-l,X=l)[/latex]
Sada iskoristiš nezavisnost od X i Y pa je
[latex]\sum_{l=0}^{m_1}P(Y=k-l)P(X=l)[/latex]
Taj izraz je 0 za l>k pa dalje imaš
[latex]\sum_{l=0}^{k}P(Y=k-l)P(X=l)=\sum_{l=0}^{k}{m_2 \choose k-l}p^{k-l}q^{m_2-k+l} {m_1 \choose l}p^l q^{m_1-l}=[/latex]
[latex]p^k q^{m_2+m_1-k}\sum_{l=0}^k {m_2 \choose k-l}{m_1 \choose l}[/latex]
pa upotrijebiš Vandermondeovu konvoluciju
[latex]{m_1+m_2 \choose k}p^k q^{(m_1+m_2)-k}[/latex]
što znači da je
X+Y~B(m1+m2,p)
Sada čitaš odozada prema naprijed i mislim da bi to trebalo biti to.
| LSSD (napisa): | Znas li rijesenje slijedeceg:
Neka su X i Y nezavisne cjelobrojne nenegativne slucajne varijable takve da je X+Y binomna sa parametrima (n,p). Dokazite da postoje m1,m2 takvi da je m1+m2=n, X je binomna s parametrima (m1,p), a Y binomna s parametrima (m2,p).
Znam da je zbroj dvije nezavisne binomne binomna, ali me zanima kako ide ova obratna konstrukcija:) |
Počneš od X~B(m1,p), Y~B(m2,p). Tada X+Y prima vrijednosti od 0 do m1+m2.
Sada je neki 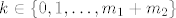 , ,
pa je
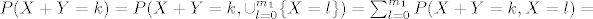
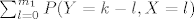
Sada iskoristiš nezavisnost od X i Y pa je
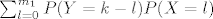
Taj izraz je 0 za l>k pa dalje imaš
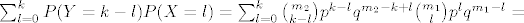
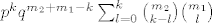
pa upotrijebiš Vandermondeovu konvoluciju
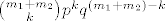
što znači da je
X+Y~B(m1+m2,p)
Sada čitaš odozada prema naprijed i mislim da bi to trebalo biti to.
_________________
The Dude Abides
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 15:35 uto, 18. 9. 2007 Naslov: Postano: 15:35 uto, 18. 9. 2007 Naslov: |
    |
|
|
@goranm: ako mozes raspisati taj slucaj unatrag
unaprijed hvala
@goranm: ako mozes raspisati taj slucaj unatrag
unaprijed hvala
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
Kobra
Forumaš(ica)

Pridružen/a: 03. 02. 2005. (10:23:52)
Postovi: (48)16
Spol: 
Lokacija: Ferenščica/Podstrana
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 16:18 uto, 18. 9. 2007 Naslov: Postano: 16:18 uto, 18. 9. 2007 Naslov: |
    |
|
|
Neka X+Y=Z~B(n=m1+m2,p). Tada je
[latex]P(Z=k)={n \choose k}p^k q^{n-k}={m_1 + m_2 \choose k}p^k q^{(m_1+m_2) - k}.[/latex]
Na ovaj zadnji binomni koeficijent primjenimo Vandermondeovu konvoluciju pa je
[latex]{m_1 + m_2 \choose k}p^k q^{(m_1+m_2) - k}=\sum_{l=0}^{k}{m_1 \choose k-l}{m_2 \choose l}p^k q^{m_1+m_2-k}.[/latex]
Sada taj izraz pomnožimo s [latex]1=p^lp^{-l}, 1=q^lq^{-l}[/latex] i malo sredimo i dobijemo da je
[latex]p^kq^{m_1+m_2-k}=p^{k-l}q^{m_2-k+l}p^lq^{m_1-l}[/latex]
i ako jednom pridružimo binomni koeficijent [latex]{m_2 \choose k-l}[/latex], a drugom [latex]{m_1 \choose l}[/latex], onda izrazi
[latex]{m_2 \choose k-l}p^{k-l}q^{m_2-k+l}[/latex] i [latex]{m_1 \choose l}p^lq^{m_1-l}[/latex] odgovaraju razdiobama binomnih slučajnih varijabli koje nazovemo X i Y, gdje X ima parametre m1 i p, a Y m2 i p.
Sada je
[latex]{m_2 \choose k-l}p^{k-l}q^{m_2-k+l}=P(Y=k-l)[/latex], a [latex]{m_1 \choose l}p^lq^{m_1-l}=P(X=l).[/latex]
pa kada to vratimo nazad u onu sumu, vrijedi
[latex]\sum_{l=0}^{m_1}P(Y=k-l)P(X=l)[/latex], a to je
[latex]\sum_{l=0}^{m_1}P(Y=k-l,X=l)[/latex] ako i samo ako su X i Y nezavisne, što znamo iz pretpostavke zadatka.
Sada tu sumu pretvorimo u uniju po X pa je
[latex]\sum_{l=0}^{m_1}P(Y=k-l,X=l)=P(Y=k-X,\cup_{l=0}^{m_1}\{X=l\})=\\P(X+Y=k)=P(Z=k)[/latex]
što znači da postoje X~B(m1,p) i Y~B(m2,p) tako da je Z=X+Y~B(m1+m2,p).
Btw. ja nisam slušao slučajne procese, ovakvi zadaci su se na UVISu radili i na vježbama se rješio točno takav, samo obratni slučaj (X,Y binomne s param. k i l,p -> X+Y binomna s par. k+l,p).
@Kobra: Sigurno bi se moglo i s funkcijama izvodnicama, ali mislim da bi se opet sve svelo na računanje s nekim sumama što je skoro pa analogno ovome gore. :)
Neka X+Y=Z~B(n=m1+m2,p). Tada je

Na ovaj zadnji binomni koeficijent primjenimo Vandermondeovu konvoluciju pa je
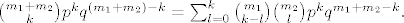
Sada taj izraz pomnožimo s 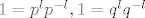 i malo sredimo i dobijemo da je i malo sredimo i dobijemo da je
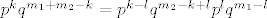
i ako jednom pridružimo binomni koeficijent 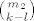 , a drugom , a drugom 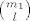 , onda izrazi , onda izrazi
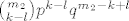 i i 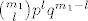 odgovaraju razdiobama binomnih slučajnih varijabli koje nazovemo X i Y, gdje X ima parametre m1 i p, a Y m2 i p. odgovaraju razdiobama binomnih slučajnih varijabli koje nazovemo X i Y, gdje X ima parametre m1 i p, a Y m2 i p.
Sada je
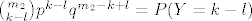 , a , a 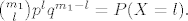
pa kada to vratimo nazad u onu sumu, vrijedi
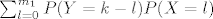 , a to je , a to je
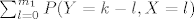 ako i samo ako su X i Y nezavisne, što znamo iz pretpostavke zadatka. ako i samo ako su X i Y nezavisne, što znamo iz pretpostavke zadatka.
Sada tu sumu pretvorimo u uniju po X pa je
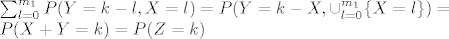
što znači da postoje X~B(m1,p) i Y~B(m2,p) tako da je Z=X+Y~B(m1+m2,p).
Btw. ja nisam slušao slučajne procese, ovakvi zadaci su se na UVISu radili i na vježbama se rješio točno takav, samo obratni slučaj (X,Y binomne s param. k i l,p → X+Y binomna s par. k+l,p).
@Kobra: Sigurno bi se moglo i s funkcijama izvodnicama, ali mislim da bi se opet sve svelo na računanje s nekim sumama što je skoro pa analogno ovome gore. 
_________________
The Dude Abides
|
|
| [Vrh] |
|
Kobra
Forumaš(ica)

Pridružen/a: 03. 02. 2005. (10:23:52)
Postovi: (48)16
Spol: 
Lokacija: Ferenščica/Podstrana
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 17:15 uto, 18. 9. 2007 Naslov: Postano: 17:15 uto, 18. 9. 2007 Naslov: |
    |
|
|
[quote="Anonymous"]Samo da provjerim: ako su X i Y nezavisne slucajne varijable, tada su max{X,Y} i min{X,Y} takodjer nezavisne?
Ovo nije vezano za diskusiju gore:)[/quote]
Zapiši max{X,Y} kao [latex]\frac{X+Y}{2}+\frac{|X-Y|}{2}[/latex]
i min{X,Y} kao [latex]\frac{X+Y}{2}-\frac{|X-Y|}{2}[/latex] pa probaj provjeriti nezavisnost. :)
| Anonymous (napisa): | Samo da provjerim: ako su X i Y nezavisne slucajne varijable, tada su max{X,Y} i min{X,Y} takodjer nezavisne?
Ovo nije vezano za diskusiju gore:) |
Zapiši max{X,Y} kao 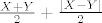
i min{X,Y} kao 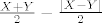 pa probaj provjeriti nezavisnost. pa probaj provjeriti nezavisnost. 
_________________
The Dude Abides
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 18:21 uto, 18. 9. 2007 Naslov: Postano: 18:21 uto, 18. 9. 2007 Naslov: |
    |
|
|
Niste dobro procitali zadatak, on ne trazi da se dokaze da ako je Z binomna sa parametrima n,p, da tada ako Z=X+Y, onda Y,X nuzno binomne, nego on trazi da se dokaze da postoje binomne sa parametrima m_1,m_2, td n=m_1+m_2. To je puno jednostavnije.
Ipak ne mogu skuziti slucaj za n=1. Mislim da na tome "pada", stoga bi odgovor bio ne. No, pola zadataka je cudno zadano, pa nikad ne znas, treba pitati asistenta,
Niste dobro procitali zadatak, on ne trazi da se dokaze da ako je Z binomna sa parametrima n,p, da tada ako Z=X+Y, onda Y,X nuzno binomne, nego on trazi da se dokaze da postoje binomne sa parametrima m_1,m_2, td n=m_1+m_2. To je puno jednostavnije.
Ipak ne mogu skuziti slucaj za n=1. Mislim da na tome "pada", stoga bi odgovor bio ne. No, pola zadataka je cudno zadano, pa nikad ne znas, treba pitati asistenta,
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:47 uto, 18. 9. 2007 Naslov: Postano: 19:47 uto, 18. 9. 2007 Naslov: |
    |
|
|
Možda je asistent zaboravio napomenuti da je n e N\{1}.
Za slučaj n=1, binomna prelazi u Bernoullievu, pa je X+Y Bernoullieva, a onda je, [u]nagađam[/u], varijabla X Bernoullieva, a Y konstanta (jednaka nuli) s vjerojatnošću 1, tj. P(Y=0)=1 pa se umjesto Y može pisati 0 (tako nešto slično je napravljeno u dokazu teorema da ako je koef korelacije između X i Y=+/ - 1, onda je Y afina fja. od X) što bi značilo da Y nije binomna pa tvrdnja ne vrijedi.
Možda je asistent zaboravio napomenuti da je n e N\{1}.
Za slučaj n=1, binomna prelazi u Bernoullievu, pa je X+Y Bernoullieva, a onda je, nagađam, varijabla X Bernoullieva, a Y konstanta (jednaka nuli) s vjerojatnošću 1, tj. P(Y=0)=1 pa se umjesto Y može pisati 0 (tako nešto slično je napravljeno u dokazu teorema da ako je koef korelacije između X i Y=+/ - 1, onda je Y afina fja. od X) što bi značilo da Y nije binomna pa tvrdnja ne vrijedi.
_________________
The Dude Abides
|
|
| [Vrh] |
|
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 21:38 uto, 18. 9. 2007 Naslov: Postano: 21:38 uto, 18. 9. 2007 Naslov: |
    |
|
|
[quote="Mr.Doe"]... To je puno jednostavnije. ...[/quote]
ako je jednostavnije objasni nam.
mi tvrdimo (malo modificirao Kobrinu izjavu):
[quote="Kobra&GauSs_"] Ako je zbroj dviju nezavisnih nenegativnih cjelobrojnih sl. varijabli X i Y binomna sl- varijabla s parametrima (n,p) , tada su nužno i X i Y binomne sl. varijable s parametrima (m1,p) odnosno (m2,p) t.d. m1+m2=n. [/quote]
a zadatak kaze:
[quote="Zadatak"] Neka su X i Y nezavisne cjelobrojne nenegativne slucajne varijable takve da je X+Y binomna sa parametrima (n,p). Dokazite da postoje m1,m2 takvi da je m1+m2=n, X je binomna s parametrima (m1,p), a Y binomna s parametrima (m2,p). [/quote]
gdje tocno grijesimo?
| Mr.Doe (napisa): | | ... To je puno jednostavnije. ... |
ako je jednostavnije objasni nam.
mi tvrdimo (malo modificirao Kobrinu izjavu):
| Kobra&GauSs_ (napisa): | | Ako je zbroj dviju nezavisnih nenegativnih cjelobrojnih sl. varijabli X i Y binomna sl- varijabla s parametrima (n,p) , tada su nužno i X i Y binomne sl. varijable s parametrima (m1,p) odnosno (m2,p) t.d. m1+m2=n. |
a zadatak kaze:
| Zadatak (napisa): | | Neka su X i Y nezavisne cjelobrojne nenegativne slucajne varijable takve da je X+Y binomna sa parametrima (n,p). Dokazite da postoje m1,m2 takvi da je m1+m2=n, X je binomna s parametrima (m1,p), a Y binomna s parametrima (m2,p). |
gdje tocno grijesimo?
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 20:22 pon, 24. 9. 2007 Naslov: Postano: 20:22 pon, 24. 9. 2007 Naslov: |
    |
|
|
[quote="Anonymous"]Da li netko zna definiciju stohastickog procesa?[/quote]
To je familija slucajnih varijabli definiranih na istom vjerojatnosnom prostoru indeksiranih po nekom skupu. Najcesce |N ili |R
| Anonymous (napisa): | | Da li netko zna definiciju stohastickog procesa? |
To je familija slucajnih varijabli definiranih na istom vjerojatnosnom prostoru indeksiranih po nekom skupu. Najcesce |N ili |R
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 15:21 sub, 24. 11. 2007 Naslov: Postano: 15:21 sub, 24. 11. 2007 Naslov: |
    |
|
|
[quote="Rok 19.9.2007."]
Zad [b]2[/b]:
Pretpostavimo da vjerojatnost da danas kisi iznosi 0.3 ako je jucer bilo
suncano i prekjucer bilo suncano, odnosno 0.6 ako je ili jucer ili prekjucer
kisilo. Neka V_{n} oznacava vrijeme u danu n te neka K oznacava stanje
za kisu, S za sunce. (V_{n}; n>=0) nije Markovljev lanac,
ali X_{n}=(V_{n}, V_{n-1}) jest Markovljev lanac s prostorom stanja
{KK, KS, SK, SS}.
a) Nadji matricu prijelaza Markovljevog lanca (X_{n}; n>=0).
b) Izracunaj vjerojatnost da ce kisiti u srijedu ako nije kisilo ni u nedjelju
ni u ponedjeljak.
[/quote]
E sada, sto mene mori?
Ne mogu nikako ispuniti Matricu prijelaza. Smatram da mi nedostaje podataka.
ovo je ono sto sam uspio ispuniti:
[code:1]
KK KS SK SS
KK 0 0
KS 0 0 0.6 0.4
SK 0.6 0.4 0 0
SS 0 0 0.3 0.7
[/code:1]
kako pronaci ostale vrijednosti?
| Rok 19.9.2007. (napisa): |
Zad 2:
Pretpostavimo da vjerojatnost da danas kisi iznosi 0.3 ako je jucer bilo
suncano i prekjucer bilo suncano, odnosno 0.6 ako je ili jucer ili prekjucer
kisilo. Neka V_{n} oznacava vrijeme u danu n te neka K oznacava stanje
za kisu, S za sunce. (V_{n}; n>=0) nije Markovljev lanac,
ali X_{n}=(V_{n}, V_{n-1}) jest Markovljev lanac s prostorom stanja
{KK, KS, SK, SS}.
a) Nadji matricu prijelaza Markovljevog lanca (X_{n}; n>=0).
b) Izracunaj vjerojatnost da ce kisiti u srijedu ako nije kisilo ni u nedjelju
ni u ponedjeljak.
|
E sada, sto mene mori?
Ne mogu nikako ispuniti Matricu prijelaza. Smatram da mi nedostaje podataka.
ovo je ono sto sam uspio ispuniti:
| Kod: |
KK KS SK SS
KK 0 0
KS 0 0 0.6 0.4
SK 0.6 0.4 0 0
SS 0 0 0.3 0.7
|
kako pronaci ostale vrijednosti?
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
|
















