| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
mali skup
Gost
|
 Postano: 14:33 sri, 10. 10. 2007 Naslov: Re: Jedinstvenost praznog skupa Postano: 14:33 sri, 10. 10. 2007 Naslov: Re: Jedinstvenost praznog skupa |
    |
|
|
[quote="Silver Surfer"]Nešto mi nije jasno. Kod dokaza jedinstvenosti praznog skupa uzmu se dva prazna skupa. Tada se pretpostavi da su različiti, a to znači da postoji element u jednom koji nije u drugom a to je kontradikcija jer prazan skup. Dobro. E, a ako pretpostavimo da su jednaki tada znači da je [b]svaki[/b] element iz prvog i u drugom skupu, pa ne vodi li onda i to do kontradikcije jer u praznom skupu nema elemenata?
[/quote]
pa i je svaki element iz prvog ujedno u drugom, jer kad tako ne bi bilo ...
naravno, ovo "svaki" ni po čemu ne implicira da "postoji neki" :wink:
| Silver Surfer (napisa): | Nešto mi nije jasno. Kod dokaza jedinstvenosti praznog skupa uzmu se dva prazna skupa. Tada se pretpostavi da su različiti, a to znači da postoji element u jednom koji nije u drugom a to je kontradikcija jer prazan skup. Dobro. E, a ako pretpostavimo da su jednaki tada znači da je svaki element iz prvog i u drugom skupu, pa ne vodi li onda i to do kontradikcije jer u praznom skupu nema elemenata?
|
pa i je svaki element iz prvog ujedno u drugom, jer kad tako ne bi bilo ...
naravno, ovo "svaki" ni po čemu ne implicira da "postoji neki" 
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 14:36 sri, 10. 10. 2007 Naslov: Re: Jedinstvenost praznog skupa Postano: 14:36 sri, 10. 10. 2007 Naslov: Re: Jedinstvenost praznog skupa |
    |
|
|
[quote="Silver Surfer"]Nešto mi nije jasno. Kod dokaza jedinstvenosti praznog skupa uzmu se dva prazna skupa. Tada se pretpostavi da su različiti, a to znači da postoji element u jednom koji nije u drugom a to je kontradikcija jer prazan skup. Dobro. E, a ako pretpostavimo da su jednaki tada znači da je svaki element iz prvog i u drugom skupu, pa ne vodi li onda i to do kontradikcije jer u praznom skupu nema elemenata?
Još me zanima, kad bi recimo oba slučaja stvarno vodila do kontradikcije što bi to onda značilo? Da ne možemo pretpostaviti da postoje dva prazna skupa? Ili nešto drugo?
Hvala[/quote]
Formula [latex]\forall x (x \in \emptyset \rightarrow P(x))[/latex] je uvijek istinita, neovisno o forumli [latex]P(x)[/latex] (po definiciji implikacije), budući je formula [latex]x \in \emptyset[/latex] lažna po definiciji praznog skupa (a "laž povlači sve").
Sada pretpostavimo da su [latex]\emptyset[/latex] i [latex]\emptyset'[/latex] prazni skupovi (tj. zadovoljavaju [latex]\forall x (x \not \in \emptyset) [/latex] i [latex]\forall x (x \not \in \emptyset') [/latex]. Želimo dokazati da je [latex]\emptyset=\emptyset'[/latex]. Po aksiomu ekstenzionalnosti trebamo pokazati [latex]\forall x (x \in \emptyset \leftrightarrow x \in \emptyset')[/latex]. Budući je za svako [latex]x[/latex] svaka od formula u ekvivalenciji lažna, to je ekvivalencija istinita, pa je formula [latex]\forall x (x \in \emptyset \leftrightarrow x \in \emptyset')[/latex] istinita, te je [latex]\emptyset=\emptyset'[/latex]
| Silver Surfer (napisa): | Nešto mi nije jasno. Kod dokaza jedinstvenosti praznog skupa uzmu se dva prazna skupa. Tada se pretpostavi da su različiti, a to znači da postoji element u jednom koji nije u drugom a to je kontradikcija jer prazan skup. Dobro. E, a ako pretpostavimo da su jednaki tada znači da je svaki element iz prvog i u drugom skupu, pa ne vodi li onda i to do kontradikcije jer u praznom skupu nema elemenata?
Još me zanima, kad bi recimo oba slučaja stvarno vodila do kontradikcije što bi to onda značilo? Da ne možemo pretpostaviti da postoje dva prazna skupa? Ili nešto drugo?
Hvala |
Formula 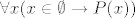 je uvijek istinita, neovisno o forumli je uvijek istinita, neovisno o forumli 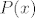 (po definiciji implikacije), budući je formula (po definiciji implikacije), budući je formula 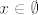 lažna po definiciji praznog skupa (a "laž povlači sve"). lažna po definiciji praznog skupa (a "laž povlači sve").
Sada pretpostavimo da su  i i 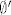 prazni skupovi (tj. zadovoljavaju prazni skupovi (tj. zadovoljavaju 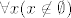 i i 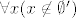 . Želimo dokazati da je . Želimo dokazati da je 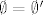 . Po aksiomu ekstenzionalnosti trebamo pokazati . Po aksiomu ekstenzionalnosti trebamo pokazati 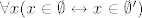 . Budući je za svako . Budući je za svako  svaka od formula u ekvivalenciji lažna, to je ekvivalencija istinita, pa je formula svaka od formula u ekvivalenciji lažna, to je ekvivalencija istinita, pa je formula 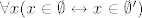 istinita, te je istinita, te je 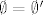
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
 Postano: 8:50 sub, 13. 10. 2007 Naslov: Postano: 8:50 sub, 13. 10. 2007 Naslov: |
    |
|
|
Samo jedno malo pitanje, može li se pisati tako samo [latex]\forall x[/latex], ne treba biti od kuda su ti x-evi?
Što se tiče mog drugog pitanja, ovo o konveksnosti. Ovako:
Neka je U ravnina i a,b iz U. Segment [a,b] jest skup svih točaka pravca koji ide kroz točke a i b (različite), koje se nalaze između a i b, uključivši i točke a, b.
Skup K podskup od U je konveksan, ako zajedno sa bilo koje dvije točke a, b iz K u K leži i njihova spojnica, tj. a, b iz K povlači [a,b] podskup od K.
I ja nikako ne znam kako iz ovoga zaključiti koji uvjeti trebaju vrijediti da bi unija dvaju konveksnih skupova bila konveksan skup ili recimo da bi komplement konveksnog skupa bio konveksan skup???
Samo jedno malo pitanje, može li se pisati tako samo 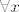 , ne treba biti od kuda su ti x-evi? , ne treba biti od kuda su ti x-evi?
Što se tiče mog drugog pitanja, ovo o konveksnosti. Ovako:
Neka je U ravnina i a,b iz U. Segment [a,b] jest skup svih točaka pravca koji ide kroz točke a i b (različite), koje se nalaze između a i b, uključivši i točke a, b.
Skup K podskup od U je konveksan, ako zajedno sa bilo koje dvije točke a, b iz K u K leži i njihova spojnica, tj. a, b iz K povlači [a,b] podskup od K.
I ja nikako ne znam kako iz ovoga zaključiti koji uvjeti trebaju vrijediti da bi unija dvaju konveksnih skupova bila konveksan skup ili recimo da bi komplement konveksnog skupa bio konveksan skup???
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 10:11 sub, 13. 10. 2007 Naslov: Postano: 10:11 sub, 13. 10. 2007 Naslov: |
    |
|
|
[quote="Silver Surfer"]Samo jedno malo pitanje, može li se pisati tako samo [latex]\forall x[/latex], ne treba biti od kuda su ti x-evi?[/quote]
Ti si programer, je l' da? :D
Ne treba ti, jer imas izraz [latex]x \in \emptyset \rightarrow \dots[/latex] sto znaci "ako je [i]x[/i] iz praznog skupa, onda...", pa te ne zanimaju ostali [i]x[/i]-evi (za njih je tvrdnja uvijek istinita jer je lijeva strana implikacije lazna, pa oni ne utjecu na istinitost cijele tvrdnje). ;)
[quote="Silver Surfer"]I ja nikako ne znam kako iz ovoga zaključiti koji uvjeti trebaju vrijediti da bi unija dvaju konveksnih skupova bila konveksan skup ili recimo da bi komplement konveksnog skupa bio konveksan skup???[/quote]
Hint za uniju: pogledaj zatvorenje konveksnih skupova. Sto znas o njihovom presjeku (ako unija (ni)je konveksna)? :-k A sto znas o odnosu spojnice [[i]a[/i], [i]b[/i]] i presjeka tih konveksnih skupova ako [i]a[/i] i [i]b[/i] nisu u istom od njih dva? :-k
| Silver Surfer (napisa): | Samo jedno malo pitanje, može li se pisati tako samo 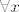 , ne treba biti od kuda su ti x-evi? , ne treba biti od kuda su ti x-evi? |
Ti si programer, je l' da? 
Ne treba ti, jer imas izraz 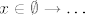 sto znaci "ako je x iz praznog skupa, onda...", pa te ne zanimaju ostali x-evi (za njih je tvrdnja uvijek istinita jer je lijeva strana implikacije lazna, pa oni ne utjecu na istinitost cijele tvrdnje). sto znaci "ako je x iz praznog skupa, onda...", pa te ne zanimaju ostali x-evi (za njih je tvrdnja uvijek istinita jer je lijeva strana implikacije lazna, pa oni ne utjecu na istinitost cijele tvrdnje). 
| Silver Surfer (napisa): | | I ja nikako ne znam kako iz ovoga zaključiti koji uvjeti trebaju vrijediti da bi unija dvaju konveksnih skupova bila konveksan skup ili recimo da bi komplement konveksnog skupa bio konveksan skup??? |
Hint za uniju: pogledaj zatvorenje konveksnih skupova. Sto znas o njihovom presjeku (ako unija (ni)je konveksna)?  A sto znas o odnosu spojnice [a, b] i presjeka tih konveksnih skupova ako a i b nisu u istom od njih dva? A sto znas o odnosu spojnice [a, b] i presjeka tih konveksnih skupova ako a i b nisu u istom od njih dva? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
 Postano: 12:58 sub, 13. 10. 2007 Naslov: Postano: 12:58 sub, 13. 10. 2007 Naslov: |
    |
|
|
Nisam programer, ali volio bih biti :D
Kuzim za tu implikaciju, ali sto je s ovim [latex]\forall x (x \not \in \emptyset)[/latex]? Jel se to smije tako napisati?
Ma znam jedino da je presjek dvaju konveksnih skupova konveksni skup. Koji god uvjet pokušam, uvijek nađem protuprimjer. Mogu bit neomeđeni, mogu bit disjunktni, svašta... A opet unija definitivno nije uvijek konveksna. Očito mi fali nekog većeg znanja :(
E, i hvala vsego 8)
Nisam programer, ali volio bih biti 
Kuzim za tu implikaciju, ali sto je s ovim 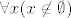 ? Jel se to smije tako napisati? ? Jel se to smije tako napisati?
Ma znam jedino da je presjek dvaju konveksnih skupova konveksni skup. Koji god uvjet pokušam, uvijek nađem protuprimjer. Mogu bit neomeđeni, mogu bit disjunktni, svašta... A opet unija definitivno nije uvijek konveksna. Očito mi fali nekog većeg znanja 
E, i hvala vsego 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 15:41 sub, 13. 10. 2007 Naslov: Postano: 15:41 sub, 13. 10. 2007 Naslov: |
    |
|
|
[quote="Silver Surfer"]Kuzim za tu implikaciju, ali sto je s ovim [latex]\forall x (x \not \in \emptyset)[/latex]? Jel se to smije tako napisati?[/quote]
Smije. :) Nije nesto sto mozes "opisati programerski" (aka "protrci po skupu iz kojeg je x i provjeri tvrdnju"); zato sam mislio da si programer. :)
[quote="Silver Surfer"]Ma znam jedino da je presjek dvaju konveksnih skupova konveksni skup. Koji god uvjet pokušam, uvijek nađem protuprimjer. Mogu bit neomeđeni, mogu bit disjunktni, svašta... A opet unija definitivno nije uvijek konveksna. Očito mi fali nekog većeg znanja :([/quote]
Pazi, naglasih: [b]zatvorenja[/b] skupova. :) Zatvorenja skupova (pricamo o realnoj ravnini) se ili sijeku ili je izmedju rupa (dakle, ne dodiruju se). 8) Ako imas izmedju rupu, onda ti unija nije zatvorena. 8) Ostaje slucaj ako nigdje nema "rupe", tj. ako svaki [[i]a[/i], [i]b[/i]] (gdje su [i]a[/i] i [i]b[/i] iz razlicitih skupova) prolazi presjekom tih zatvorenja. :) Tada je unija zatvorenja konveksna. 8) Na zalost, moguce je da sama unija skupova nije zatvorena, pa ti treba jos malo promisljanja. :( Primjer (na pravcu, da bude lakse): [0,5> i <5,7]. :) Ostavljam tebi da se igras s tim. ;)
A mozda je onaj tko vam je to zadao mislio na neki skroz drugi kriterij, pa ja zapravo krivo hintiram... :neznam:
| Silver Surfer (napisa): | Kuzim za tu implikaciju, ali sto je s ovim 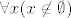 ? Jel se to smije tako napisati? ? Jel se to smije tako napisati? |
Smije.  Nije nesto sto mozes "opisati programerski" (aka "protrci po skupu iz kojeg je x i provjeri tvrdnju"); zato sam mislio da si programer. Nije nesto sto mozes "opisati programerski" (aka "protrci po skupu iz kojeg je x i provjeri tvrdnju"); zato sam mislio da si programer. 
| Silver Surfer (napisa): | Ma znam jedino da je presjek dvaju konveksnih skupova konveksni skup. Koji god uvjet pokušam, uvijek nađem protuprimjer. Mogu bit neomeđeni, mogu bit disjunktni, svašta... A opet unija definitivno nije uvijek konveksna. Očito mi fali nekog većeg znanja  |
Pazi, naglasih: zatvorenja skupova.  Zatvorenja skupova (pricamo o realnoj ravnini) se ili sijeku ili je izmedju rupa (dakle, ne dodiruju se). Zatvorenja skupova (pricamo o realnoj ravnini) se ili sijeku ili je izmedju rupa (dakle, ne dodiruju se).  Ako imas izmedju rupu, onda ti unija nije zatvorena. Ako imas izmedju rupu, onda ti unija nije zatvorena.  Ostaje slucaj ako nigdje nema "rupe", tj. ako svaki [a, b] (gdje su a i b iz razlicitih skupova) prolazi presjekom tih zatvorenja. Ostaje slucaj ako nigdje nema "rupe", tj. ako svaki [a, b] (gdje su a i b iz razlicitih skupova) prolazi presjekom tih zatvorenja.  Tada je unija zatvorenja konveksna. Tada je unija zatvorenja konveksna.  Na zalost, moguce je da sama unija skupova nije zatvorena, pa ti treba jos malo promisljanja. Na zalost, moguce je da sama unija skupova nije zatvorena, pa ti treba jos malo promisljanja.  Primjer (na pravcu, da bude lakse): [0,5> i <5,7]. Primjer (na pravcu, da bude lakse): [0,5> i <5,7].  Ostavljam tebi da se igras s tim. Ostavljam tebi da se igras s tim. 
A mozda je onaj tko vam je to zadao mislio na neki skroz drugi kriterij, pa ja zapravo krivo hintiram... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
 Postano: 9:57 pon, 15. 10. 2007 Naslov: Postano: 9:57 pon, 15. 10. 2007 Naslov: |
    |
|
|
Prihvaćam da se smije, ali mi se i dalje nekako čini malo neprecizno.
Što se tiče konveksnosti, ja sam isto dok sam razmišljao dolazio do toga da ne smije biti rupa, ali nisam znao kako to objasniti matematički, i onda sam isto došao do takvog primjera, recimo [0,5> i [5,7]. I onda sam odustao.
Inače, zadatak je zadao profesor Kurepa u knjizi "Uvod u matematiku", zato me i ne brine što ne znam riješiti zadatak.:D Jednog dana ću možda doći od rješenja.
Prihvaćam da se smije, ali mi se i dalje nekako čini malo neprecizno.
Što se tiče konveksnosti, ja sam isto dok sam razmišljao dolazio do toga da ne smije biti rupa, ali nisam znao kako to objasniti matematički, i onda sam isto došao do takvog primjera, recimo [0,5> i [5,7]. I onda sam odustao.
Inače, zadatak je zadao profesor Kurepa u knjizi "Uvod u matematiku", zato me i ne brine što ne znam riješiti zadatak. Jednog dana ću možda doći od rješenja. Jednog dana ću možda doći od rješenja.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
 Postano: 17:14 pon, 29. 10. 2007 Naslov: Postano: 17:14 pon, 29. 10. 2007 Naslov: |
    |
|
|
Kad sam tu već počeo o konveksnosti, imam još jedno pitanje, nikako ne mogu dokazati da je skup U[a,b] za a,b iz A konveksan, gdje je A neki skup (ne mora biti konveksan). Može li mi netko pomoći? Probao sam dokazati i direktno i tako da pretpostavim da nije konveksan, ali nikako ne ide. :?
Kad sam tu već počeo o konveksnosti, imam još jedno pitanje, nikako ne mogu dokazati da je skup U[a,b] za a,b iz A konveksan, gdje je A neki skup (ne mora biti konveksan). Može li mi netko pomoći? Probao sam dokazati i direktno i tako da pretpostavim da nije konveksan, ali nikako ne ide. 
|
|
| [Vrh] |
|
|









