| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 15:51 uto, 30. 10. 2007 Naslov: Postano: 15:51 uto, 30. 10. 2007 Naslov: |
    |
|
|
Sto se [i]k-[/i]-kombinacija tice, u "Kombinatornoj i diskretnoj matematici" prof. Veljana (izdanje Algoritma), na strani 61, pise da je [latex]\textstyle r \geq 0[/latex] (njemu je [i]r[/i] ovo sto je vama [i]k[/i]). :) Besides, zasto 0-kombinacija ne bi bila validan pojam? :-k
Mozda ne bi bilo lose da upozoris asistenta. :? Ne toliko da je sad nesto jako krivo ili tocno (stvar je dogovora hoces li uzeti nulu ili ne), nego da se asistenti usklade, jer ce sve grupe (valjda) imati zajednicki kolokvij. :)
Sto se k--kombinacija tice, u "Kombinatornoj i diskretnoj matematici" prof. Veljana (izdanje Algoritma), na strani 61, pise da je 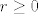 (njemu je r ovo sto je vama k). (njemu je r ovo sto je vama k).  Besides, zasto 0-kombinacija ne bi bila validan pojam? Besides, zasto 0-kombinacija ne bi bila validan pojam? 
Mozda ne bi bilo lose da upozoris asistenta.  Ne toliko da je sad nesto jako krivo ili tocno (stvar je dogovora hoces li uzeti nulu ili ne), nego da se asistenti usklade, jer ce sve grupe (valjda) imati zajednicki kolokvij. Ne toliko da je sad nesto jako krivo ili tocno (stvar je dogovora hoces li uzeti nulu ili ne), nego da se asistenti usklade, jer ce sve grupe (valjda) imati zajednicki kolokvij. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 18:29 uto, 30. 10. 2007 Naslov: Postano: 18:29 uto, 30. 10. 2007 Naslov: |
    |
|
|
[quote="ma"]hm :-k
zašto bi netko morao imati svih 30 zadataka. jedina bitna stvar je da svaki zadatak daš jednom studentu. prvi zadatak možeš podijeliti na 10 načina, drugi na 10, treći na 10, ... , trideseti na 10. ukupno načina: [latex]10^{30}[/latex]. :)[/quote]
Krivo sam skužio zadatak, onaj dio "svaki od 30 zadataka mora dobiti točno jedan student", sada je OK.
| ma (napisa): | hm 
zašto bi netko morao imati svih 30 zadataka. jedina bitna stvar je da svaki zadatak daš jednom studentu. prvi zadatak možeš podijeliti na 10 načina, drugi na 10, treći na 10, ... , trideseti na 10. ukupno načina: 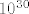 . .  |
Krivo sam skužio zadatak, onaj dio "svaki od 30 zadataka mora dobiti točno jedan student", sada je OK.
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
Nori
Forumaš(ica)
Pridružen/a: 01. 10. 2006. (18:41:07)
Postovi: (E5)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
 Postano: 22:14 uto, 30. 10. 2007 Naslov: Postano: 22:14 uto, 30. 10. 2007 Naslov: |
    |
|
|
[quote="Nori"][quote="arya"]
11.(n povrh 3)*((n-3) povrh 2)*( (r-(n-3)*k+n-5-1) povrh (r-(n-3)*k))
[/quote]
može pliz objašnjenje, meni je ispalo slično, samo u ovom zadnjem (r-(n-3)*k)-1)...[/quote]
ovo ne valja...
ukratko, vidio sam kod puno ljudi da su maknuli tri prazne, onda
napunili sve preostale s k, onda
odabrali dvije u kojima ce ostati tocno k i onda
napunili ostale s preostalim kuglicama...
to ne valja jer neke slucajeve brojite previse puta
primjer: odabrali smo da ce u kutijama A i B ostati tocno k kuglica i ostale kuglice rasporedimo na neki nacin. recimo da se desilo da ce i kutija C ostati sa samo k kuglica( sto je vrlo realno i moguce)
drugi put odaberemo da ce u kutijama A i C ostati tocno k kuglica i ostale rasporedimo na neki nacin i bas se desi da u kutiji B ostane tocno k kuglica a u ostalim kutijama je isti raspored ko i prije. onda ste ovaj slucaj brojali dvaput i tu nesto ne valja...
rjesenje koje smo mi uspjeli danas smisliti je koristeci komplement( bar u ovom dijelu s k kuglica i te finte)
RJESENJE:
(a,b) je a povrh b
prvo odaberemo (n,3) kutije koje ce bit prazne i to je ok jer nam se to ne mijesa s nicim...
onda u sve ostale kutije stavimo k kuglica. nek je r=(n-3)k+l gdje je l>=0
sad cemo imati 3 slucaja...
1. l<=n-5.
sad kako god rasporedili preostale kuglice se ne moze desiti da u barem dvije kutije nema tocno k kuglica pa nam svaki raspored pase.
rjesenje ovdje je (n,3)(l+n-3-1,l) tj. (n,3)(n+l-4,l)
2. l=n-4
sad jedini slucajevi koji nam ne pasu je ako se u jednoj kutiji nalazi k kuglica, a u ostalih n-4 se nalazi k+1 kuglica. takvih slucajeva ima n-3(jer tu jednu posebnu kutiju mozemo ocito odabrati na n-3 nacina)
broj svih slucajeva je (l+n-3-1,l) pa je rjesenje (n,3)((2n-8,n-4)-(n-3)) jer ovdje tocno znamo koliki je l pa smo ga uvrstili u rjesenje...
3. l>=n-3
svih slucajeva ima (l+n-3-1,l), a nepovoljni slucajevi su kad
3.a) u svakoj kutiji ima bar k+1 kuglica
sto znaci da baratamo s jos l-(n-3) kuglice koje mozemo na bilo koji nacin rasporediti u n-3 kutije a takvih nacina je
(l-(n-3)+n-3-1,l-(n-3)) tj. (l-1,l-n+3).
3.b)u jednoj kutiji je tocno k a u ostalima barem k+1. posebnu kutiju s k elemenata biramo na (n-3) nacina a u ostale stavljamo u svaku bar po jednu kuglicu sto nam ostavlja l-(n-4) kuglica koje moramo smjestili u n-4 kutije(jer u onu s tocno k elemenata ne stavljamo nista) a takvih nacina ima (l-(n-4)+n-4-1,l-(n-4)) tj (l-1,l-n+4) sto mnozeno s (n-3) daje
(n-3)(l-1,l-n+4).
odavdje imamo da je ukupan broj nepovoljnih slucajeva
(l-1,l-n+3) + (n-3)(l-1,l-n+4) sto kad oduzmemo od ukupnog broja slucajeva daje rjesenje u trecem slucaju
(n,3)[(l+n-4,l)-(l-1,l-n+3)-(n-3)(l-1,l-n+4)]
greske su lako moguce pa ispravke odmah uvazavam ako ce se kom dat citati :D, al mislim da je cijela ideja ok...
| Nori (napisa): | | arya (napisa): |
11.(n povrh 3)*((n-3) povrh 2)*( (r-(n-3)*k+n-5-1) povrh (r-(n-3)*k))
|
može pliz objašnjenje, meni je ispalo slično, samo u ovom zadnjem (r-(n-3)*k)-1)... |
ovo ne valja...
ukratko, vidio sam kod puno ljudi da su maknuli tri prazne, onda
napunili sve preostale s k, onda
odabrali dvije u kojima ce ostati tocno k i onda
napunili ostale s preostalim kuglicama...
to ne valja jer neke slucajeve brojite previse puta
primjer: odabrali smo da ce u kutijama A i B ostati tocno k kuglica i ostale kuglice rasporedimo na neki nacin. recimo da se desilo da ce i kutija C ostati sa samo k kuglica( sto je vrlo realno i moguce)
drugi put odaberemo da ce u kutijama A i C ostati tocno k kuglica i ostale rasporedimo na neki nacin i bas se desi da u kutiji B ostane tocno k kuglica a u ostalim kutijama je isti raspored ko i prije. onda ste ovaj slucaj brojali dvaput i tu nesto ne valja...
rjesenje koje smo mi uspjeli danas smisliti je koristeci komplement( bar u ovom dijelu s k kuglica i te finte)
RJESENJE:
(a,b) je a povrh b
prvo odaberemo (n,3) kutije koje ce bit prazne i to je ok jer nam se to ne mijesa s nicim...
onda u sve ostale kutije stavimo k kuglica. nek je r=(n-3)k+l gdje je l>=0
sad cemo imati 3 slucaja...
1. l⇐n-5.
sad kako god rasporedili preostale kuglice se ne moze desiti da u barem dvije kutije nema tocno k kuglica pa nam svaki raspored pase.
rjesenje ovdje je (n,3)(l+n-3-1,l) tj. (n,3)(n+l-4,l)
2. l=n-4
sad jedini slucajevi koji nam ne pasu je ako se u jednoj kutiji nalazi k kuglica, a u ostalih n-4 se nalazi k+1 kuglica. takvih slucajeva ima n-3(jer tu jednu posebnu kutiju mozemo ocito odabrati na n-3 nacina)
broj svih slucajeva je (l+n-3-1,l) pa je rjesenje (n,3)((2n-8,n-4)-(n-3)) jer ovdje tocno znamo koliki je l pa smo ga uvrstili u rjesenje...
3. l>=n-3
svih slucajeva ima (l+n-3-1,l), a nepovoljni slucajevi su kad
3.a) u svakoj kutiji ima bar k+1 kuglica
sto znaci da baratamo s jos l-(n-3) kuglice koje mozemo na bilo koji nacin rasporediti u n-3 kutije a takvih nacina je
(l-(n-3)+n-3-1,l-(n-3)) tj. (l-1,l-n+3).
3.b)u jednoj kutiji je tocno k a u ostalima barem k+1. posebnu kutiju s k elemenata biramo na (n-3) nacina a u ostale stavljamo u svaku bar po jednu kuglicu sto nam ostavlja l-(n-4) kuglica koje moramo smjestili u n-4 kutije(jer u onu s tocno k elemenata ne stavljamo nista) a takvih nacina ima (l-(n-4)+n-4-1,l-(n-4)) tj (l-1,l-n+4) sto mnozeno s (n-3) daje
(n-3)(l-1,l-n+4).
odavdje imamo da je ukupan broj nepovoljnih slucajeva
(l-1,l-n+3) + (n-3)(l-1,l-n+4) sto kad oduzmemo od ukupnog broja slucajeva daje rjesenje u trecem slucaju
(n,3)[(l+n-4,l)-(l-1,l-n+3)-(n-3)(l-1,l-n+4)]
greske su lako moguce pa ispravke odmah uvazavam ako ce se kom dat citati  , al mislim da je cijela ideja ok... , al mislim da je cijela ideja ok...
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
Fisher
Forumaš(ica)

Pridružen/a: 09. 02. 2007. (23:38:24)
Postovi: (41)16
Lokacija: split
|
 Postano: 0:22 sri, 31. 10. 2007 Naslov: Postano: 0:22 sri, 31. 10. 2007 Naslov: |
    |
|
|
može netko dati rješenje 12.?
ja sam to shvatio kao broj permutacija multiskupa {a1^k, a2^k, ... , an^k} gdje a-ove međusobno ne razlikujemo (odatle onaj n! u nazivniku koji me zbunjuje).. al malo mi je nejasno to rješenje, s tim ponavljanjem i neponavljanjem.. ima neki drugi način?
može netko dati rješenje 12.?
ja sam to shvatio kao broj permutacija multiskupa {a1^k, a2^k, ... , an^k} gdje a-ove međusobno ne razlikujemo (odatle onaj n! u nazivniku koji me zbunjuje).. al malo mi je nejasno to rješenje, s tim ponavljanjem i neponavljanjem.. ima neki drugi način?
_________________
.. sve bi seke ljubile mornare, ali mame, mame brane to ..
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
 Postano: 0:59 sri, 31. 10. 2007 Naslov: Postano: 0:59 sri, 31. 10. 2007 Naslov: |
    |
|
|
da, 11. očito ne valja, sad vidim :? rješenje mi se baš nije dalo čitat, ali, goc, svejedno karma++ :)
što se tiče dvanaestog... ja to gledah kao podjelu k*n različitih zadataka u n grupa s k zadataka ( različitih, naravno)... prvu grupu biraš na (kn povrh k) načina, drugu na ((kn-k) povrh k), itd. do zadnje koju biraš na (k povrh k) načina... poredak grupa nam nije bitan, pa to sve moramo podijeliti sa n!... i sad kad se to malo raspiše, dobije se točno onaj izraz u zadatku...
ajd nek mi sad netko kaže da ni to ne valja :lol:
i na kraju, jel ima netko osim mene da je u def. zapisao da se prazan skup ne računa kao kombinacija? fisher, kak tebi ide ta definicija? :)
da, 11. očito ne valja, sad vidim  rješenje mi se baš nije dalo čitat, ali, goc, svejedno karma++ rješenje mi se baš nije dalo čitat, ali, goc, svejedno karma++ 
što se tiče dvanaestog... ja to gledah kao podjelu k*n različitih zadataka u n grupa s k zadataka ( različitih, naravno)... prvu grupu biraš na (kn povrh k) načina, drugu na ((kn-k) povrh k), itd. do zadnje koju biraš na (k povrh k) načina... poredak grupa nam nije bitan, pa to sve moramo podijeliti sa n!... i sad kad se to malo raspiše, dobije se točno onaj izraz u zadatku...
ajd nek mi sad netko kaže da ni to ne valja 
i na kraju, jel ima netko osim mene da je u def. zapisao da se prazan skup ne računa kao kombinacija? fisher, kak tebi ide ta definicija? 
_________________ kalendar 
  |
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
mala
Forumaš(ica)


Pridružen/a: 10. 10. 2006. (16:13:20)
Postovi: (2A)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
j.b.i.n.s.h.
Forumaš(ica)

Pridružen/a: 24. 06. 2007. (10:28:11)
Postovi: (1B)16
|
 Postano: 11:45 sri, 31. 10. 2007 Naslov: Postano: 11:45 sri, 31. 10. 2007 Naslov: |
    |
|
|
A i ja se sjetim pisat zadaću u 5 do 12 (doslovno),
ali ako netko ima još energije...
Zadatak 11.
klasika, odaberemo 3 kutije koje ćemo ostaviti prazne
rasporedimo u svaku od preostalih n-3 po k kuglica
sada nam je na raspolaganju ostalo r-k*(n-3) što je nenegativno iz uvijeta
imamo n-3 kutije, zamislimo da su prazne (jer sve imaju isto elemenata pa nam nije ni bitno) i želimo u njih rasporediti ovih r-k*(n-3) kuglica t.d. da nam barem 2 ostanu prazne pa gledamo komplement:
samo jedna je prazna
niti jedna nije prazna
rješenje bi tako bilo:
SVI RASPOREDI-KAD JE 1 PRAZNA-KAD NITI JEDNA NIJE PRAZNA
broj svih rasporeda je broj rješenja jednadžbe od n-3 nepoznanice koje su sve nenegativne
kad je jedna prazna odaberemo tu jednu od n-3 pa rješavamo jedn. od n-4 nep od kojih svaka veća ili jednaka 1
kada niti jedna nije prazna n-3 nepoznanice, svaka veća ili jednaka 1
i to sad, kao, štima za svaki broj kuglica
upitno bi možda bilo kada nam ne bi više ostalo kuglica, ali je tada broj svih rasporeda 1 (0+0+0.....=0), a ostale jedn nemaju rj
analogno i za sve "male brojeve"
nisam uspjela naći grešku, poželjno je da me netko ispravi
A i ja se sjetim pisat zadaću u 5 do 12 (doslovno),
ali ako netko ima još energije...
Zadatak 11.
klasika, odaberemo 3 kutije koje ćemo ostaviti prazne
rasporedimo u svaku od preostalih n-3 po k kuglica
sada nam je na raspolaganju ostalo r-k*(n-3) što je nenegativno iz uvijeta
imamo n-3 kutije, zamislimo da su prazne (jer sve imaju isto elemenata pa nam nije ni bitno) i želimo u njih rasporediti ovih r-k*(n-3) kuglica t.d. da nam barem 2 ostanu prazne pa gledamo komplement:
samo jedna je prazna
niti jedna nije prazna
rješenje bi tako bilo:
SVI RASPOREDI-KAD JE 1 PRAZNA-KAD NITI JEDNA NIJE PRAZNA
broj svih rasporeda je broj rješenja jednadžbe od n-3 nepoznanice koje su sve nenegativne
kad je jedna prazna odaberemo tu jednu od n-3 pa rješavamo jedn. od n-4 nep od kojih svaka veća ili jednaka 1
kada niti jedna nije prazna n-3 nepoznanice, svaka veća ili jednaka 1
i to sad, kao, štima za svaki broj kuglica
upitno bi možda bilo kada nam ne bi više ostalo kuglica, ali je tada broj svih rasporeda 1 (0+0+0.....=0), a ostale jedn nemaju rj
analogno i za sve "male brojeve"
nisam uspjela naći grešku, poželjno je da me netko ispravi
_________________
...joined because i needed some help...
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
|



















