| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:08 čet, 8. 11. 2007 Naslov: Postano: 17:08 čet, 8. 11. 2007 Naslov: |
    |
|
|
Ovo je čisto po sjećanju... (nek me netko ispravi ak je krivo)
Skup izvodnica nekog prostora bi bio neki skup vektora koji razapinje cijeli prostor (može biti i linearno zavisan skup; ako je nezavisan, onda je taj skup i baza prostora)...pa se onda uzme bilo koji vektor (proizvoljan) iz nekog prostora i pokuša prikazati kao lin kombinacija vektora iz tog skupa za koji tvrdimo da je skup izvodnica...ako se svaki vektor (dakle taj proizvoljni) može prikazati kao lin komb tih vektora onda je taj skup skup izvodnica za taj prostor.
Ovo je čisto po sjećanju... (nek me netko ispravi ak je krivo)
Skup izvodnica nekog prostora bi bio neki skup vektora koji razapinje cijeli prostor (može biti i linearno zavisan skup; ako je nezavisan, onda je taj skup i baza prostora)...pa se onda uzme bilo koji vektor (proizvoljan) iz nekog prostora i pokuša prikazati kao lin kombinacija vektora iz tog skupa za koji tvrdimo da je skup izvodnica...ako se svaki vektor (dakle taj proizvoljni) može prikazati kao lin komb tih vektora onda je taj skup skup izvodnica za taj prostor.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
 Postano: 17:27 čet, 8. 11. 2007 Naslov: Postano: 17:27 čet, 8. 11. 2007 Naslov: |
    |
|
|
evo ti skup vektora ( (1,0,0), (0,1,0), (0,0,1) ), haj ti tu sad provjeri dal je ovo skup izvodnica za neki vektorski prostor
evo ti skup vektora ( (1,0,0), (0,1,0), (0,0,1) ), haj ti tu sad provjeri dal je ovo skup izvodnica za neki vektorski prostor
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:44 čet, 8. 11. 2007 Naslov: Postano: 17:44 čet, 8. 11. 2007 Naslov: |
    |
|
|
Ovisi za koji prostor...ako je za R3 onda je jer je (x,y,z)=x(1,0,0)+y(0,1,0)+z(0,0,1), al ak je za R4 recimo onda nije...i ne znam kak je za komplexne prostore...mislim da ni za njih nije, al nisam siguran...
Ovisi za koji prostor...ako je za R3 onda je jer je (x,y,z)=x(1,0,0)+y(0,1,0)+z(0,0,1), al ak je za R4 recimo onda nije...i ne znam kak je za komplexne prostore...mislim da ni za njih nije, al nisam siguran...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 17:47 čet, 8. 11. 2007 Naslov: Postano: 17:47 čet, 8. 11. 2007 Naslov: |
    |
|
|
Recimo, za [latex]\mathbb{R}^3[/latex] nad poljem [latex]\mathbb{R}[/latex], uzmeš neki [latex]v \in \mathbb{R}^3[/latex], [latex]v = \left( {a_1 ,a_2 ,a_3 } \right) = a_1 \left( {1,0,0} \right) + a_2 \left( {0,1,0} \right) + a_3 \left( {0,0,1} \right)[/latex], pa se on može prikazat kao linearna kombinacija vektora iz tog skupa. Kako je [latex]v[/latex] bio proizvoljan iz [latex]\mathbb{R}^3[/latex], zaključujemo da se svaki vektor iz tog prostora može prikazati kao linearna kombinacija vekotra iz tog skupa, pa je on skup izvodnica za taj vektorski prostor. Nad poljem [latex]\mathbb{C}[/latex] to isto vrijedi (iako sam prije napiso glupost), ali recimo nad [latex]\mathbb{Q}[/latex] ne vrijedi (za vektor [latex]\left( {\sqrt 2 ,0,0} \right)[/latex] ne postoje takvi koefcijenti [latex]\alpha ,\beta ,\gamma \in \mathbb{Q}[/latex] da vrijedi [latex]\left( {\sqrt 2 ,0,0} \right) = \alpha \left( {1,0,0} \right) + \beta \left( {0,1,0} \right) + \gamma \left( {0,0,1} \right)[/latex]).
Eto
Recimo, za 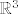 nad poljem nad poljem  , uzmeš neki , uzmeš neki  , , 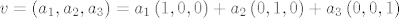 , pa se on može prikazat kao linearna kombinacija vektora iz tog skupa. Kako je , pa se on može prikazat kao linearna kombinacija vektora iz tog skupa. Kako je  bio proizvoljan iz bio proizvoljan iz 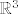 , zaključujemo da se svaki vektor iz tog prostora može prikazati kao linearna kombinacija vekotra iz tog skupa, pa je on skup izvodnica za taj vektorski prostor. Nad poljem , zaključujemo da se svaki vektor iz tog prostora može prikazati kao linearna kombinacija vekotra iz tog skupa, pa je on skup izvodnica za taj vektorski prostor. Nad poljem  to isto vrijedi (iako sam prije napiso glupost), ali recimo nad to isto vrijedi (iako sam prije napiso glupost), ali recimo nad  ne vrijedi (za vektor ne vrijedi (za vektor 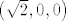 ne postoje takvi koefcijenti ne postoje takvi koefcijenti 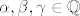 da vrijedi da vrijedi 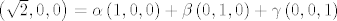 ). ).
Eto
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 17:54 čet, 8. 11. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:57 čet, 8. 11. 2007 Naslov: Postano: 17:57 čet, 8. 11. 2007 Naslov: |
    |
|
|
Isto...samo onda imaš prostor matrica...taj prostor je dimenzije 4 pa ti trebaju najmanje 4 vektora u skupu (2^2) da bi taj skup uopće bio kandidat za skup izvodnica...pa uzmeš proizvoljnu matricu i probaš je napisati kao lin komb vektora iz tog skupa...ako uspiješ - bingo.
Isto...samo onda imaš prostor matrica...taj prostor je dimenzije 4 pa ti trebaju najmanje 4 vektora u skupu (2^2) da bi taj skup uopće bio kandidat za skup izvodnica...pa uzmeš proizvoljnu matricu i probaš je napisati kao lin komb vektora iz tog skupa...ako uspiješ - bingo.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 18:01 čet, 8. 11. 2007 Naslov: Postano: 18:01 čet, 8. 11. 2007 Naslov: |
    |
|
|
Prostor [latex]M_n \left( F \right)[/latex] nad recimo istim poljem [latex]F[/latex] se može identificirati sa [latex]F^{n^2 }[/latex] nad istim poljem.
Recimo, [latex]M_2 \left( \mathbb{R} \right)[/latex] nad [latex]\mathbb{R}[/latex] se može shvatiti kao [latex]\mathbb{R}^4[/latex] nad [latex]\mathbb{R}[/latex] na sljedeći način:
[latex]f:M_2 \left( \mathbb{R} \right) \to \mathbb{R}^4[/latex], [latex]f\left( {\left[ {\begin{array}{*{20}c}
a & b \\
c & d \\
\end{array} } \right]} \right) = \left( {a,b,c,d} \right)[/latex], je izomorfizam vektorskih prostora, čuva strukturu.
Dakle, kad radiš s matricama, prepišeš prvi redak, drugi odma desno od njega i tak dalje, dobiješ nešt iz [latex]\mathbb{R}^n[/latex] i onda si na domaćem terenu.
Prostor 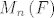 nad recimo istim poljem nad recimo istim poljem 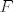 se može identificirati sa se može identificirati sa 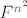 nad istim poljem. nad istim poljem.
Recimo, 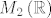 nad nad  se može shvatiti kao se može shvatiti kao 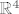 nad nad  na sljedeći način: na sljedeći način:
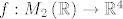 , , 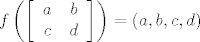 , je izomorfizam vektorskih prostora, čuva strukturu. , je izomorfizam vektorskih prostora, čuva strukturu.
Dakle, kad radiš s matricama, prepišeš prvi redak, drugi odma desno od njega i tak dalje, dobiješ nešt iz  i onda si na domaćem terenu. i onda si na domaćem terenu.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 18:05 čet, 8. 11. 2007 Naslov: Postano: 18:05 čet, 8. 11. 2007 Naslov: |
    |
|
|
Opa, sry, onda sam se zaletio.
Skup [latex]
\left\{ {\left[ {\begin{array}{*{20}c}
1 & 2 \\
1 & 1 \\
\end{array} } \right],\left[ {\begin{array}{*{20}c}
0 & 0 \\
0 & 0 \\
\end{array} } \right]} \right\}[/latex] nije skup izvodnica za [latex]M_2 \left( \mathbb{R} \right)[/latex] jer [latex]\left[ {\begin{array}{*{20}c}
a & b \\
c & d \\
\end{array} } \right] = \alpha \left[ {\begin{array}{*{20}c}
1 & 2 \\
1 & 1 \\
\end{array} } \right] + \beta \left[ {\begin{array}{*{20}c}
0 & 0 \\
0 & 0 \\
\end{array} } \right] = \left[ {\begin{array}{*{20}c}
\alpha & {2\alpha } \\
\alpha & \alpha \\
\end{array} } \right][/latex] se navedena jednakost nemože postići za proizvoljne [latex]a,b,c,d \in \mathbb{R}[/latex], recimo za [latex]a = b = c = 0,d = 1[/latex] mora istovremeno vrijediti [latex]\alpha = a = \frac{b}
{2} = c = 0[/latex] i [latex]\alpha = d = 1[/latex]
Opa, sry, onda sam se zaletio.
Skup 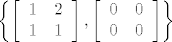 nije skup izvodnica za nije skup izvodnica za 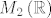 jer jer 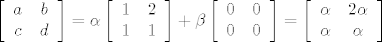 se navedena jednakost nemože postići za proizvoljne se navedena jednakost nemože postići za proizvoljne 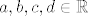 , recimo za , recimo za 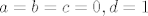 mora istovremeno vrijediti mora istovremeno vrijediti 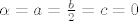 i i 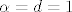
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 18:13 čet, 8. 11. 2007; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Markec
Forumaš(ica)

Pridružen/a: 20. 02. 2003. (14:49:45)
Postovi: (134)16
Spol: 
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
Markec
Forumaš(ica)

Pridružen/a: 20. 02. 2003. (14:49:45)
Postovi: (134)16
Spol: 
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 18:42 čet, 8. 11. 2007 Naslov: Postano: 18:42 čet, 8. 11. 2007 Naslov: |
    |
|
|
[quote="anam"]ok mislim da sam čak dobila da mi ovaj moj skup je skup izvodnica, a hoćeš mi još samo reći koliko je dim Mmxn, treba mi za zad, a to trebamo također dokazat a budući da to ne znam ne mogu riješit niš[/quote]
[latex]E_{ij} : = \begin{array}{*{20}c}
1 \\
\vdots \\
i \\
\vdots \\
m \\
\end{array} \mathop {\left[ {\begin{array}{*{20}c}
0 & \cdots & 0 & \cdots & 0 \\
\vdots & \ddots & \vdots & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu
\raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} & \vdots \\
0 & \cdots & 1 & \cdots & 0 \\
\vdots & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu
\raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} & \vdots & \ddots & \vdots \\
0 & \cdots & 0 & \cdots & 0 \\
\end{array} } \right]}\limits^{\begin{array}{*{20}c}
1 & \cdots & j & \cdots & n \\
\end{array} }[/latex]. Sada je [latex]\left\{ {E_{ij} :i \in \left\{ {1,...,m} \right\},j \in \left\{ {1,...,n} \right\}} \right\}[/latex] baza za taj prostor, ima [latex]m \cdot n[/latex] elemenata pa se vidi dimenzija.
| anam (napisa): | | ok mislim da sam čak dobila da mi ovaj moj skup je skup izvodnica, a hoćeš mi još samo reći koliko je dim Mmxn, treba mi za zad, a to trebamo također dokazat a budući da to ne znam ne mogu riješit niš |
 . Sada je . Sada je 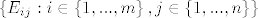 baza za taj prostor, ima baza za taj prostor, ima 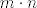 elemenata pa se vidi dimenzija. elemenata pa se vidi dimenzija.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
|











