| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:48 čet, 8. 11. 2007 Naslov: Postano: 18:48 čet, 8. 11. 2007 Naslov: |
    |
|
|
Ajme koji crtež... :shock:
Uglavnom, kanonska baza za prostor M(m,n) je skup matrica E(i,j) (matrice koje imaju 1 na mjestu (i,j), a ostalo nule, i ide od 1 do m , j od 1 do n) pa pošto tih matrica ima m*n to ti je dimenzija. Za prostor kvadratnih matrica reda n je dimenzija n^2 (pošto je m=n).
Ajme koji crtež... 
Uglavnom, kanonska baza za prostor M(m,n) je skup matrica E(i,j) (matrice koje imaju 1 na mjestu (i,j), a ostalo nule, i ide od 1 do m , j od 1 do n) pa pošto tih matrica ima m*n to ti je dimenzija. Za prostor kvadratnih matrica reda n je dimenzija n^2 (pošto je m=n).
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 20:15 čet, 8. 11. 2007 Naslov: Postano: 20:15 čet, 8. 11. 2007 Naslov: |
    |
|
|
baza - linearno nezavisan [b]skup[/b] vektora koji razapinje prostor
dimenzija - [b]broj[/b] elemenata vektora baze, tj kardinalni broj lin nez skupa koji razapinje prostor
baza - linearno nezavisan skup vektora koji razapinje prostor
dimenzija - broj elemenata vektora baze, tj kardinalni broj lin nez skupa koji razapinje prostor
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:22 čet, 8. 11. 2007 Naslov: Postano: 22:22 čet, 8. 11. 2007 Naslov: |
    |
|
|
[quote="anam"]Ma mene ti samo zanima koliko ce sada ova moja baza imati elemenata jer imam zad nadopuni tam nekakav skup do baze a ne znam koliko trebam elemenata dopunit al ok sad sam valjda skužila, bar neš[/quote]
Ako se radi o onom zadatku s matricama koje si ranije spomenula, trebalo bi ti 2 vektora (tj matrice) jer je dimenzija tog prostora 4. Pošto ti je jedna od matrica u skupu nul-matrica, ipak moraš dodat 3 vektora (matrice). Pa onda probaš neke matrice ubacit u taj skup i provjeravaš dal je taj skup lin nezavisan...kad dobiješ skup od 4 elementa koji je lin nezavisan, to je to. A dodaješ najjednostavnije moguće, matrice kanonske baze, one E(i,j)...možeš 1 po 1 ili odmah neke 3...I svaki put kad dodaš provjeriš lin nez...puno ima pisanja,al tak ti je to... :lol:
| anam (napisa): | | Ma mene ti samo zanima koliko ce sada ova moja baza imati elemenata jer imam zad nadopuni tam nekakav skup do baze a ne znam koliko trebam elemenata dopunit al ok sad sam valjda skužila, bar neš |
Ako se radi o onom zadatku s matricama koje si ranije spomenula, trebalo bi ti 2 vektora (tj matrice) jer je dimenzija tog prostora 4. Pošto ti je jedna od matrica u skupu nul-matrica, ipak moraš dodat 3 vektora (matrice). Pa onda probaš neke matrice ubacit u taj skup i provjeravaš dal je taj skup lin nezavisan...kad dobiješ skup od 4 elementa koji je lin nezavisan, to je to. A dodaješ najjednostavnije moguće, matrice kanonske baze, one E(i,j)...možeš 1 po 1 ili odmah neke 3...I svaki put kad dodaš provjeriš lin nez...puno ima pisanja,al tak ti je to... 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 23:12 čet, 8. 11. 2007 Naslov: Postano: 23:12 čet, 8. 11. 2007 Naslov: |
    |
|
|
A tako, jedan rutiniziran način rješavanja je sljedeći:
Želiš skup [latex]\left\{ {\left[ {\begin{array}{*{20}c}
1 & 2 \\
1 & 1 \\
\end{array} } \right],\left[ {\begin{array}{*{20}c}
0 & 0 \\
0 & 0 \\
\end{array} } \right]} \right\}[/latex] dopunit do baze. Da bi se to desilo odma znaš da nul-matrica tu nema šta radit.
Gledaš skup [latex]\left\{ {\left[ {\begin{array}{*{20}c}
1 & 2 \\
1 & 1 \\
\end{array} } \right]} \right\} \cup \left\{ {E_{11} ,E_{12} ,E_{21} ,E_{22} } \right\}[/latex]. To je skup izvodnica za dani prostor jer sadrži bazu u sebi (namjerno nadopuniš kanonskom bazom).
Želiš ga reducirat do baze, s tim da znaš da moraš zadržat sve elemente iz ovog prvog skupa.
Sad radiš onu identifikaciju sa [latex]\mathbb{R}^4[/latex] što sam prije pričo pa dobiješ skup [latex]\left\{ {\left( {1,1,2,1} \right),\left( {1,0,0,0} \right),\left( {0,1,0,0} \right),\left( {0,0,1,0} \right),\left( {0,0,0,1} \right)} \right\}[/latex]. Staviš ih sad lijepo sve u matricu, jedan na drugi:
[latex]\begin{array}{*{20}c}
{1.} \\
{2.} \\
{3.} \\
{4.} \\
{5.} \\
\end{array} \left[ {\begin{array}{*{20}c}
1 & 2 & 1 & 1 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array} } \right] \sim \begin{array}{*{20}c}
{1.} \\
{2.} \\
{3.} \\
{4.} \\
{5.} \\
\end{array} \left[ {\begin{array}{*{20}c}
1 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array} } \right][/latex][latex] \sim \begin{array}{*{20}c}
{1.} \\
{2.} \\
{3.} \\
{4.} \\
{5.} \\
\end{array} \left[ {\begin{array}{*{20}c}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array} } \right] \sim \begin{array}{*{20}c}
{1.} \\
{3.} \\
{4.} \\
{5.} \\
{2.} \\
\end{array} \left[ {\begin{array}{*{20}c}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 \\
\end{array} } \right][/latex]. Cilj ti je dobit blok jedinične matrice ko ova na kraju, a sa strane "pamtiš" o kojoj se matrici radi (s tim da imaš na umu da 1. redak, onaj koji predstavlja matricu [latex]{\left[ {\begin{array}{*{20}c}
1 & 2 \\
1 & 1 \\
\end{array} } \right]}[/latex], mora ostat unutra). Sad mirno možeš zaključit da 1., 3., 4. i 5. matrica čine bazu, dakle [latex]\left\{ {\left[ {\begin{array}{*{20}c}
1 & 2 \\
1 & 1 \\
\end{array} } \right]} \right\} \cup \left\{ {E_{12} ,E_{21} ,E_{22} } \right\}[/latex] je baza za dani prostor.
A tako, jedan rutiniziran način rješavanja je sljedeći:
Želiš skup 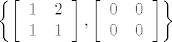 dopunit do baze. Da bi se to desilo odma znaš da nul-matrica tu nema šta radit. dopunit do baze. Da bi se to desilo odma znaš da nul-matrica tu nema šta radit.
Gledaš skup 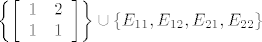 . To je skup izvodnica za dani prostor jer sadrži bazu u sebi (namjerno nadopuniš kanonskom bazom). . To je skup izvodnica za dani prostor jer sadrži bazu u sebi (namjerno nadopuniš kanonskom bazom).
Želiš ga reducirat do baze, s tim da znaš da moraš zadržat sve elemente iz ovog prvog skupa.
Sad radiš onu identifikaciju sa 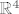 što sam prije pričo pa dobiješ skup što sam prije pričo pa dobiješ skup 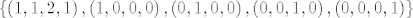 . Staviš ih sad lijepo sve u matricu, jedan na drugi: . Staviš ih sad lijepo sve u matricu, jedan na drugi:
  . Cilj ti je dobit blok jedinične matrice ko ova na kraju, a sa strane "pamtiš" o kojoj se matrici radi (s tim da imaš na umu da 1. redak, onaj koji predstavlja matricu . Cilj ti je dobit blok jedinične matrice ko ova na kraju, a sa strane "pamtiš" o kojoj se matrici radi (s tim da imaš na umu da 1. redak, onaj koji predstavlja matricu 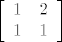 , mora ostat unutra). Sad mirno možeš zaključit da 1., 3., 4. i 5. matrica čine bazu, dakle , mora ostat unutra). Sad mirno možeš zaključit da 1., 3., 4. i 5. matrica čine bazu, dakle 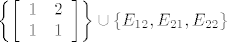 je baza za dani prostor. je baza za dani prostor.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 23:16 čet, 8. 11. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 23:16 čet, 8. 11. 2007 Naslov: Postano: 23:16 čet, 8. 11. 2007 Naslov: |
    |
|
|
Nisam siguran, al ne znam ni dal još znaju kaj su Gaussove eliminacije...sjećam se da smo mi to baš onak ružno ručno morali radit...nadopunjavat, izbacivat itd...
Nisam siguran, al ne znam ni dal još znaju kaj su Gaussove eliminacije...sjećam se da smo mi to baš onak ružno ručno morali radit...nadopunjavat, izbacivat itd...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 1:30 pet, 9. 11. 2007 Naslov: Postano: 1:30 pet, 9. 11. 2007 Naslov: |
    |
|
|
Evo još jedan koristan način, malo kad se uhodaš.
Da ne nadopunjavaš i izbacuješ....
Vidiš da ti se [latex]
{\left[ {\begin{array}{*{20}c}
1 & 2 \\
1 & 1 \\
\end{array} } \right]}
[/latex]
nemože nikako prikazati kao linearna kombinacija bilo koje tri kanonske matrice, pa jednostavno uzmeš recimo
[latex]
{\left[ {\begin{array}{*{20}c}
1 & 0 \\
0 & 0 \\
\end{array} } \right]} [/latex],[latex]\ {\left[ {\begin{array}{*{20}c}
0 & 1 \\
0 & 0 \\
\end{array} } \right]} [/latex] i [latex]{\left[ {\begin{array}{*{20}c}
0 & 0 \\
1 & 0 \\
\end{array} } \right]} [/latex] i sad tvrdiš da je to baza za prostor [latex] M_2(R) [/latex]. Pokažeš da su te 4 matrice linearno nezavisne, pošto je prostor dimnezije 4, bilo koji linearno nezavisan skup sa 4 elementa čini bazu toga prostora. Uoči da postupak nadopunjavanja do baze nije jedinstven jer možeš nadopuniti i s:
[latex]
{\left[ {\begin{array}{*{20}c}
1 & 0 \\
0 & 0 \\
\end{array} } \right]} [/latex],[latex]\ {\left[ {\begin{array}{*{20}c}
0 & 1 \\
0 & 0 \\
\end{array} } \right]} [/latex] i [latex]{\left[ {\begin{array}{*{20}c}
0 & 0 \\
0 & 1 \\
\end{array} } \right]} [/latex] ili u ovom slučaju bilo kojom drugom kombinacijom 3 od 4 kanonske matrice.
Međutim kada bi imala matricu [latex]
{\left[ {\begin{array}{*{20}c}
1 & 2 \\
1 & 0 \\
\end{array} } \right]}
[/latex], tada znaš da vrijedi:
[latex]
{\left[ {\begin{array}{*{20}c}
1 & 2 \\
1 & 0 \\
\end{array} } \right]} =1\cdot {\left[ {\begin{array}{*{20}c}
1 & 0 \\
0 & 0 \\
\end{array} } \right]} + 2\cdot {\left[ {\begin{array}{*{20}c}
0 & 1 \\
0 & 0 \\
\end{array} } \right]}+ 1\cdot {\left[ {\begin{array}{*{20}c}
0 & 0 \\
1 & 0 \\
\end{array} } \right]}
[/latex], zbog toga u ovome primjeru nesmiješ nadopuniti sa [latex] E_{11},E_{12},E_{21} [/latex].
Nadam se da će pomoči. :)
Evo još jedan koristan način, malo kad se uhodaš.
Da ne nadopunjavaš i izbacuješ....
Vidiš da ti se 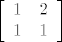
nemože nikako prikazati kao linearna kombinacija bilo koje tri kanonske matrice, pa jednostavno uzmeš recimo
 , ,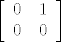 i i  i sad tvrdiš da je to baza za prostor i sad tvrdiš da je to baza za prostor 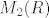 . Pokažeš da su te 4 matrice linearno nezavisne, pošto je prostor dimnezije 4, bilo koji linearno nezavisan skup sa 4 elementa čini bazu toga prostora. Uoči da postupak nadopunjavanja do baze nije jedinstven jer možeš nadopuniti i s: . Pokažeš da su te 4 matrice linearno nezavisne, pošto je prostor dimnezije 4, bilo koji linearno nezavisan skup sa 4 elementa čini bazu toga prostora. Uoči da postupak nadopunjavanja do baze nije jedinstven jer možeš nadopuniti i s:
 , ,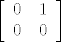 i i 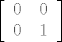 ili u ovom slučaju bilo kojom drugom kombinacijom 3 od 4 kanonske matrice. ili u ovom slučaju bilo kojom drugom kombinacijom 3 od 4 kanonske matrice.
Međutim kada bi imala matricu 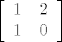 , tada znaš da vrijedi: , tada znaš da vrijedi:
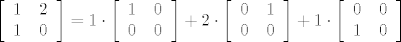 , zbog toga u ovome primjeru nesmiješ nadopuniti sa , zbog toga u ovome primjeru nesmiješ nadopuniti sa 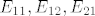 . .
Nadam se da će pomoči. 
|
|
| [Vrh] |
|
|












