u skripti imas definiciju nezavisnosti pa nema smisla prepisivati, nego evo primjer za 3 matrice 2x2
[latex]A_1= \left[ {\begin{array}{*{20}c} 1 & 2 \\ { 0} & { 1} \\ \end{array}} \right],A_2=\left[ {\begin{array}{*{20}c} 0 & 0 \\ { -1} & { 1} \\ \end{array}} \right], A_3= \left[ {\begin{array}{*{20}c} 0 & 2 \\ { 1} & { 1} \\ \end{array}} \right][/latex].
prvo postavis jednadbu [latex]aA_1+bA_2+cA_3=0[/latex] (nula je nul-matrica), tj.
[latex]a \left[ {\begin{array}{*{20}c} 1 & 2 \\ { 0} & { 1} \\ \end{array}} \right] + b \left[ {\begin{array}{*{20}c} 0 & 0 \\ { -1} & { 1} \\ \end{array}} \right] + c \left[ {\begin{array}{*{20}c} 0 & 2 \\ { 1} & { 1} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}c} 0 & 0 \\ { 0} & { 0} \\ \end{array}} \right][/latex]
[latex]\Rightarrow \left[ {\begin{array}{*{20}c} a & 2a \\ { 0} & { a} \\ \end{array}} \right] + \left[ {\begin{array}{*{20}c} 0 & 0 \\ { -b} & { b} \\ \end{array}} \right] + \left[ {\begin{array}{*{20}c} 0 & 2c \\ { c} & { c} \\ \end{array}} \right]=\left[ {\begin{array}{*{20}c} 0 & 0 \\ { 0} & { 0} \\ \end{array}} \right][/latex]
[latex]\Rightarrow \left[ {\begin{array}{*{20}c} a & {2a+2c} \\ {-b+c} & { a+b+c} \\ \end{array}} \right]=\left[ {\begin{array}{*{20}c} 0 & 0 \\ { 0} & { 0} \\ \end{array}} \right][/latex] a iz togo dobijes sustav linearnih jednadzbi:
[latex]a=0[/latex]
[latex]2a+2c=0[/latex]
[latex]-b+c=0[/latex]
[latex]a+b+c=0[/latex] , a rijesenje tog sustava je ocito jedino [latex]a=b=c=0[/latex], pa je skup [latex]\{ A_1,A_2,A_3 \} [/latex] po definiciji linearno nezavisan.
imas jos razne cake koje mozes koristiti za brze rjesavanje nekih posebnih slucajeva, al to ces pokupiti vjezbajuci
u skripti imas definiciju nezavisnosti pa nema smisla prepisivati, nego evo primjer za 3 matrice 2x2
.
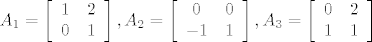prvo postavis jednadbu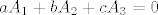 
(nula je nul-matrica), tj.
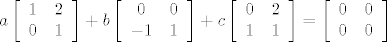
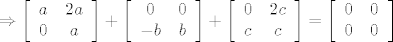
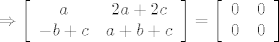a iz togo dobijes sustav linearnih jednadzbi:
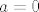
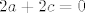
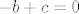
, a rijesenje tog sustava je ocito jedino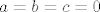 
, pa je skup 
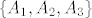po definiciji linearno nezavisan.
imas jos razne cake koje mozes koristiti za brze rjesavanje nekih posebnih slucajeva, al to ces pokupiti vjezbajuci
_________________
Rafael Mrđen
