| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 13:53 sub, 17. 11. 2007 Naslov: Postano: 13:53 sub, 17. 11. 2007 Naslov: |
    |
|
|
Što misliš pod matematički precizno? Ono traženje gdje je fja bijektivna itd?
Što misliš pod matematički precizno? Ono traženje gdje je fja bijektivna itd?
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:18 sub, 17. 11. 2007 Naslov: Postano: 14:18 sub, 17. 11. 2007 Naslov: |
    |
|
|
Pretpostavljam da pitaš za sliku i prasliku...
f:A->B , A,B podskupovi od R; A1 podskup od A; B1 podskup od B
f(A1)(slika) := { y iz B, t.d. y=f(x), x iz A1 }
f-1(B1)(praslika) := { x iz A t.d. y=f(x), y iz B1 }
To je sve po definiciji, evo riječima:
Slika nekog skupa (od A1) je skup svih funkcijskih vrijednosti tog skupa, a praslika je skup svih onih elemenata domene koji se preslikaju u tvoj skup (B1).
Nadam se da pomaže...
Pretpostavljam da pitaš za sliku i prasliku...
f:A->B , A,B podskupovi od R; A1 podskup od A; B1 podskup od B
f(A1)(slika) := { y iz B, t.d. y=f(x), x iz A1 }
f-1(B1)(praslika) := { x iz A t.d. y=f(x), y iz B1 }
To je sve po definiciji, evo riječima:
Slika nekog skupa (od A1) je skup svih funkcijskih vrijednosti tog skupa, a praslika je skup svih onih elemenata domene koji se preslikaju u tvoj skup (B1).
Nadam se da pomaže...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
 Postano: 14:45 sub, 17. 11. 2007 Naslov: Postano: 14:45 sub, 17. 11. 2007 Naslov: |
    |
|
|
[quote="Luuka"]'
Nadam se da pomaže...[/quote]
Pa, u svakom slučaju hvala na trudu... :)
Ali mislim baš na inverznu funkciju.
Npr. ovaj dio u rješenju jednog zadatka...
Uzmemo y element [4,9> i tražimo jedinstveni x element [2,3> td. y = f1|[2,3> (x) akko y = x^2. x1,2 = +- y ... x1,2 = y jer je x element [2,3>.
x = korijen iz y.
(f1|[2,3>)^-1 (y) = korijen iz y
| Luuka (napisa): | '
Nadam se da pomaže... |
Pa, u svakom slučaju hvala na trudu... 
Ali mislim baš na inverznu funkciju.
Npr. ovaj dio u rješenju jednog zadatka...
Uzmemo y element [4,9> i tražimo jedinstveni x element [2,3> td. y = f1|[2,3> (x) akko y = x^2. x1,2 = +- y ... x1,2 = y jer je x element [2,3>.
x = korijen iz y.
(f1|[2,3>)^-1 (y) = korijen iz y
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:55 sub, 17. 11. 2007 Naslov: Postano: 14:55 sub, 17. 11. 2007 Naslov: |
    |
|
|
Dakle imaš ovo:
f:[2,3> -> [4,9>
f(x)=x^2.
Sad je inverz
f{-1} : [4,9> -> [2,3>
f{-1}(y)=sqrt(x).
Pošto je ta fja bijektivna onda za svaki element kodomene postoji jedinstven element domene koji se u njega preslika.
Uzmeš neki y iz [4,9> i tražiš kamo se on preslika po inverznoj fji (f{-1}), ili uzmeš y iz [4,9> i gledaš koji x se u njega preslika po 'glavnoj' fji (f)...
@anam: Sin je pozitivan na <0,pi> pa taviš da je 0<pi/x<pi pa imaš dvije nejednadžbe...( oprez, sa x ne smiješ množit jer ne znaš kojeg je predznaka)
Dakle imaš ovo:
f:[2,3> -> [4,9>
f(x)=x^2.
Sad je inverz
f{-1} : [4,9> -> [2,3>
f{-1}(y)=sqrt(x).
Pošto je ta fja bijektivna onda za svaki element kodomene postoji jedinstven element domene koji se u njega preslika.
Uzmeš neki y iz [4,9> i tražiš kamo se on preslika po inverznoj fji (f{-1}), ili uzmeš y iz [4,9> i gledaš koji x se u njega preslika po 'glavnoj' fji (f)...
@anam: Sin je pozitivan na <0,pi> pa taviš da je 0<pi/x<pi pa imaš dvije nejednadžbe...( oprez, sa x ne smiješ množit jer ne znaš kojeg je predznaka)
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
 Postano: 15:00 sub, 17. 11. 2007 Naslov: Postano: 15:00 sub, 17. 11. 2007 Naslov: |
    |
|
|
[quote="Luuka"]Dakle imaš ovo:
f:[2,3> -> [4,9>
f(x)=x^2.
Sad je inverz
f{-1} : [4,9> -> [2,3>
f{-1}(y)=sqrt(x).
Pošto je ta fja bijektivna onda za svaki element kodomene postoji jedinstven element domene koji se u njega preslika.
Uzmeš neki y iz [4,9> i tražiš kamo se on preslika po inverznoj fji (f{-1}), ili uzmeš y iz [4,9> i gledaš koji x se u njega preslika po 'glavnoj' fji (f)...
[/quote]
Ok, hvala. :)
| Luuka (napisa): | Dakle imaš ovo:
f:[2,3> → [4,9>
f(x)=x^2.
Sad je inverz
f{-1} : [4,9> → [2,3>
f{-1}(y)=sqrt(x).
Pošto je ta fja bijektivna onda za svaki element kodomene postoji jedinstven element domene koji se u njega preslika.
Uzmeš neki y iz [4,9> i tražiš kamo se on preslika po inverznoj fji (f{-1}), ili uzmeš y iz [4,9> i gledaš koji x se u njega preslika po 'glavnoj' fji (f)...
|
Ok, hvala. 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 15:00 sub, 17. 11. 2007 Naslov: Postano: 15:00 sub, 17. 11. 2007 Naslov: |
    |
|
|
[quote="anam"]sin pi/x>0[/quote]
[latex]$\begin{align*}
\sin \frac\pi{x} > 0 &\Leftrightarrow \frac\pi{x} \in \langle2k\pi, (2k+1)\pi\rangle \Leftrightarrow x^{-1} \in \langle2k, 2k+1\rangle \\
&\Leftrightarrow x \in \langle(2k+1)^{-1}, (2k)^{-1}\rangle,\quad k\in\mathbb{Z}\end{align*}$[/latex]
@Luuka: Kako ne zna?! 0<pi/x<pi... [b]moze li[/b] x biti negativan? :grebgreb: No, fale ti ostale vrijednosti za koje je sinus (kao periodicka funkcija) pozitivan... :)
| anam (napisa): | | sin pi/x>0 |
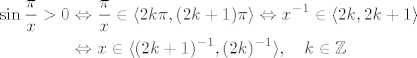
@Luuka: Kako ne zna?! 0<pi/x<pi... moze li x biti negativan?  No, fale ti ostale vrijednosti za koje je sinus (kao periodicka funkcija) pozitivan... No, fale ti ostale vrijednosti za koje je sinus (kao periodicka funkcija) pozitivan... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 15:17 sub, 17. 11. 2007 Naslov: Postano: 15:17 sub, 17. 11. 2007 Naslov: |
    |
|
|
[quote="Luuka"]To je rješenje one moje nejednadžbe, gdje sam izostavio periodičnost sinusa...pogledaj vsegino rješenje ;)[/quote]
vsegino nije dovrseno. ;) Ako uvrstis k=0, dobijes upravo <0,+oo>, tako da je djelomicno tocno. 8)
Naravno, treba jos i za negativne [i]k[/i]. :)
| Luuka (napisa): | To je rješenje one moje nejednadžbe, gdje sam izostavio periodičnost sinusa...pogledaj vsegino rješenje  |
vsegino nije dovrseno.  Ako uvrstis k=0, dobijes upravo <0,+oo>, tako da je djelomicno tocno. Ako uvrstis k=0, dobijes upravo <0,+oo>, tako da je djelomicno tocno. 
Naravno, treba jos i za negativne k. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 15:22 sub, 17. 11. 2007 Naslov: Postano: 15:22 sub, 17. 11. 2007 Naslov: |
    |
|
|
[quote="vsego"]Ako uvrstis k=0, dobijes upravo <0,+oo>, tako da je djelomicno tocno. 8)[/quote]
za k=0 dobije se <1,+oo> :wink:
I ak ćemo baš cjepidlačit trebalo bi se razdvojit kad je sinus rastuć, kad padajuć pa napisat to sve ko veliku uniju intervala... 8)
| vsego (napisa): | Ako uvrstis k=0, dobijes upravo <0,+oo>, tako da je djelomicno tocno.  |
za k=0 dobije se <1,+oo> 
I ak ćemo baš cjepidlačit trebalo bi se razdvojit kad je sinus rastuć, kad padajuć pa napisat to sve ko veliku uniju intervala... 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
|













