|
[quote="matmih"]Zadatak je :
Jeli skup [latex] \left\{(x,y)\in \mathbb{R}^2: x^2+y^2<5 \right\} [/latex]otvoren ili zatvoren?
Zanimalo me dali se to može kako dokazati pomoću neprekidne funkcije (kika je pogodila).
I ako dobijemo onakav interval u slici šta možemo zaključiti za prasliku?
Dakle funkciju sami definiramo (vjerojatno sam tu nešto zeznuo :oops: )
Uf, valjda je jasnije šta me zanima.[/quote]
probat cu ti objasniti,ne znam koliko cu uspjeti,ali pokusat cu najjednostavnije moguce:-)
ovaj tvoj skup oznaci recimo sa A.
f(x,y) definiras tako da uzmes ove x-ove i y-one sa lijeve strane nejednakosti,a ovu 5 ne diras.(znaci f(x,y)=x^2+y^2)
(a recimo i da ti je ta 5 s lijeve strane nekednaksoti bila,slobodno si ju
prebacis na desnu stranu,tako da na lijevoj imas samo nepoznanice,a na desnoj brojeve)
po tom gore intervalu,f(x,y)e (<-bes.,5>).
sad sam gledala u rjesenja od prosle god. slicnog zadatka,kojeg je prof.rijesavao( [latex] \left\{(x,y)\in \mathbb{R}^2: 2x^2+6y^2<3 \right\} [/latex]) i on je uzeo da je f(x,y)e(<-besk.,3>))
znaci,ne uzimas u obzir uvjet dal ce biti manja od nule ili ne,uzimas samo onaj koji ti je postavljen u skupu,za ostalo se nemoj zamarati :)
interval (<-bes.,5>) je otvoren.mozes zakljuciti da je
i praslika otv.intervala f-1(<-bes,5>) otvorena.
(i da si dobio da je f(x,y) element zatvorenog intervala,mozes zakljuciti da praslika zatv.intervala bi bila zatvorena)
a ta praslika je upravo onaj gornji skup A,pa zaklj.da je i A otvoren.
mozda ti ovo pomogne:napomena sa predavanja: funkcija f je neprekidna akko je za svaki otvoren podskup UcRk ,skup f-1(U) otvoren u A.
(vrijedi i za zatv.)
| matmih (napisa): | Zadatak je :
Jeli skup 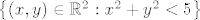 otvoren ili zatvoren? otvoren ili zatvoren?
Zanimalo me dali se to može kako dokazati pomoću neprekidne funkcije (kika je pogodila).
I ako dobijemo onakav interval u slici šta možemo zaključiti za prasliku?
Dakle funkciju sami definiramo (vjerojatno sam tu nešto zeznuo  ) )
Uf, valjda je jasnije šta me zanima. |
probat cu ti objasniti,ne znam koliko cu uspjeti,ali pokusat cu najjednostavnije moguce:-)
ovaj tvoj skup oznaci recimo sa A.
f(x,y) definiras tako da uzmes ove x-ove i y-one sa lijeve strane nejednakosti,a ovu 5 ne diras.(znaci f(x,y)=x^2+y^2)
(a recimo i da ti je ta 5 s lijeve strane nekednaksoti bila,slobodno si ju
prebacis na desnu stranu,tako da na lijevoj imas samo nepoznanice,a na desnoj brojeve)
po tom gore intervalu,f(x,y)e (←bes.,5>).
sad sam gledala u rjesenja od prosle god. slicnog zadatka,kojeg je prof.rijesavao( 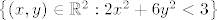 ) i on je uzeo da je f(x,y)e(←besk.,3>)) ) i on je uzeo da je f(x,y)e(←besk.,3>))
znaci,ne uzimas u obzir uvjet dal ce biti manja od nule ili ne,uzimas samo onaj koji ti je postavljen u skupu,za ostalo se nemoj zamarati 
interval (←bes.,5>) je otvoren.mozes zakljuciti da je
i praslika otv.intervala f-1(←bes,5>) otvorena.
(i da si dobio da je f(x,y) element zatvorenog intervala,mozes zakljuciti da praslika zatv.intervala bi bila zatvorena)
a ta praslika je upravo onaj gornji skup A,pa zaklj.da je i A otvoren.
mozda ti ovo pomogne:napomena sa predavanja: funkcija f je neprekidna akko je za svaki otvoren podskup UcRk ,skup f-1(U) otvoren u A.
(vrijedi i za zatv.)
|






