| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 10:18 pon, 26. 11. 2007 Naslov: Postano: 10:18 pon, 26. 11. 2007 Naslov: |
    |
|
|
[quote="LSSD"]Nedostaju ti vjerojatnosti 0.6 i 0.4. Imas dovoljno podataka jer uvjet da danas kisi ako je [b]ili jucer ili prekjucer[/b] kisilo pokriva i cinjenicu da je oba (prethodna dva ) dana kisilo.[/quote]
hmmm. meni se pak cini da tu stoji ekskluzivno ili a ne ukljucivo ili.
| LSSD (napisa): | | Nedostaju ti vjerojatnosti 0.6 i 0.4. Imas dovoljno podataka jer uvjet da danas kisi ako je ili jucer ili prekjucer kisilo pokriva i cinjenicu da je oba (prethodna dva ) dana kisilo. |
hmmm. meni se pak cini da tu stoji ekskluzivno ili a ne ukljucivo ili.
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 15:58 pon, 26. 11. 2007 Naslov: Postano: 15:58 pon, 26. 11. 2007 Naslov: |
    |
|
|
[quote="Anonymous"]Evo još jednog zadačića...
Brod ima tri navigacijska uređaja, te može ploviti ako barem dva uređaja rade. Pretpostavimo da su vremena kvarova uređaja eksponencijalno distribuirana s 1, 2/3 i 1/3. Koje je očekivano vrijeme koje brod može provesti na moru?
Hvala[/quote]
Ocekivano vrijeme prvog kvara je E[Exp(1+2/3+1/3)]=1/2 jer ustvari trazis E[min{Exp(1),Exp(2/3),Exp(1/3)}]
Ocekivano vrijeme od prvog do drugog kvara (T) razbijes na par slucajeva:
ako je prvi kvar vezan uz PRVI/DRUGI/TRECI navigavijski uredjaj
E[T]=E[min{Exp(2/3),Exp(1/3)}]*P(Exp(1)<min{Exp(2/3),Exp(1/3)}] +
E[min{Exp(1),Exp(1/3)}]*P(Exp(2/3)<min{Exp(1),Exp(1/3)}] +
E[min{Exp(1),Exp(2/3)}]*P(Exp(1/3)<min{Exp(1,Exp(2/3)}]
i sada to sve izracunas te zbrojs 1/2+E[T] ;)
| Anonymous (napisa): | Evo još jednog zadačića...
Brod ima tri navigacijska uređaja, te može ploviti ako barem dva uređaja rade. Pretpostavimo da su vremena kvarova uređaja eksponencijalno distribuirana s 1, 2/3 i 1/3. Koje je očekivano vrijeme koje brod može provesti na moru?
Hvala |
Ocekivano vrijeme prvog kvara je E[Exp(1+2/3+1/3)]=1/2 jer ustvari trazis E[min{Exp(1),Exp(2/3),Exp(1/3)}]
Ocekivano vrijeme od prvog do drugog kvara (T) razbijes na par slucajeva:
ako je prvi kvar vezan uz PRVI/DRUGI/TRECI navigavijski uredjaj
E[T]=E[min{Exp(2/3),Exp(1/3)}]*P(Exp(1)<min{Exp(2/3),Exp(1/3)}] +
E[min{Exp(1),Exp(1/3)}]*P(Exp(2/3)<min{Exp(1),Exp(1/3)}] +
E[min{Exp(1),Exp(2/3)}]*P(Exp(1/3)<min{Exp(1,Exp(2/3)}]
i sada to sve izracunas te zbrojs 1/2+E[T] 
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 19:42 uto, 27. 11. 2007 Naslov: Postano: 19:42 uto, 27. 11. 2007 Naslov: |
    |
|
|
Jos jedan:
Neka [latex](Z_n,n\geq 0)[/latex] proces grananja za koji [latex]Z_0=1,\mathbb{P}(Z_1=k)=pg^k,~k\geq 0,~p+g=1[/latex]. Neka [latex] T=\min\{n:Z_n=0\}[/latex].
(a) Izracunajte [latex]p_n=\mathbb{P}(T=n)[/latex]
(b) Za koje vrijednosti od p je [latex]\mathbb{E}[T]<+\infty[/latex]
Uspio sam naci da je (u (a)) [latex]\displaystyle p_n=\sum_{k=1}^{\infty}pg^k p_{n-1}^k,~n\geq 2[/latex], ali dalje od toga nisam, dosao, te mi ovo ne izgleda obecavajuce.
off-topic: to vsego: jer mozes staviti da za pisanje u LaTex-u koristimo $ - $ switch, jer ove sadasnje switchove je dosta naporno stalno pisati?
Jos jedan:
Neka 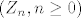 proces grananja za koji proces grananja za koji 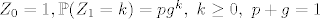 . Neka . Neka 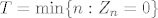 . .
(a) Izracunajte 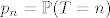
(b) Za koje vrijednosti od p je 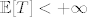
Uspio sam naci da je (u (a)) 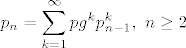 , ali dalje od toga nisam, dosao, te mi ovo ne izgleda obecavajuce. , ali dalje od toga nisam, dosao, te mi ovo ne izgleda obecavajuce.
off-topic: to vsego: jer mozes staviti da za pisanje u LaTex-u koristimo $ - $ switch, jer ove sadasnje switchove je dosta naporno stalno pisati?
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 10:14 sri, 28. 11. 2007 Naslov: Postano: 10:14 sri, 28. 11. 2007 Naslov: |
    |
|
|
[quote="Anonymous"]Brod ima tri navigacijska uređaja i dva mehaničara. Svaki od uređaja radi eksponencijalno distribuirano vrijeme s očekivanjem 30 dana, dok svaki kvar zahtijeva popravak mehaničara koji traje eksponencijalno vrijeme s očekivanim trajanjem od dva dana. Koliko postotak vremena, dugoročno, niti jedan ne radi?
Mooolim pomoc!!![/quote]
S=broj ispravnih uredjaja={0,1,2,3}
Ako imas 0 ispravnih mozes doci samo u 1 ispravni
Cekanje u stanju 0 je min{Exp{1/2},Exp{1/2}} jer imas samo dva
mehanicara koja popravljaju s ocekivanjem popravka od 2 dana.
Ocito cekas dok prvi ne popravi (neprekidno vrijeme=> ne mogu istovremeno popravit)
Zakljucujes lambda(0)=1
Ako imas 1 ispravan mozes doci u 0 ispravnih i vjerojatnost je
*=P(Exp(1/30)<min{Exp(1/2),Exp(1/2)} tj. prije se mora pokvariti
ispravni nego sto jedan od majstora popravi uredjaj.
Takodjer, mozes doci u 2 ispravna i vjerojatnost je
=1-*
U tri ispravna ocito nemos doc.
Cekanje u stanje 1 je min{Exp(1/30),Exp(1/2),Exp(1/2)}~Exp(31/30}
tj. dok se jedan ne pokvari ili ostali ne poprave
Zakljucujes lambda(1)=31/30
Napravis tako i za ostala stanja (hint: ocito iz stanja 3 mozes doc samo u stanje 2)
Sada imas matricu prijelaza diskretnog P i funkciju [b]lambda[/b]
Napravis generatorsku matricu A i izracunas stacionarnu distribuciju
te ocitas zeljeni rezultat.
| Anonymous (napisa): | Brod ima tri navigacijska uređaja i dva mehaničara. Svaki od uređaja radi eksponencijalno distribuirano vrijeme s očekivanjem 30 dana, dok svaki kvar zahtijeva popravak mehaničara koji traje eksponencijalno vrijeme s očekivanim trajanjem od dva dana. Koliko postotak vremena, dugoročno, niti jedan ne radi?
Mooolim pomoc!!! |
S=broj ispravnih uredjaja={0,1,2,3}
Ako imas 0 ispravnih mozes doci samo u 1 ispravni
Cekanje u stanju 0 je min{Exp{1/2},Exp{1/2}} jer imas samo dva
mehanicara koja popravljaju s ocekivanjem popravka od 2 dana.
Ocito cekas dok prvi ne popravi (neprekidno vrijeme⇒ ne mogu istovremeno popravit)
Zakljucujes lambda(0)=1
Ako imas 1 ispravan mozes doci u 0 ispravnih i vjerojatnost je
*=P(Exp(1/30)<min{Exp(1/2),Exp(1/2)} tj. prije se mora pokvariti
ispravni nego sto jedan od majstora popravi uredjaj.
Takodjer, mozes doci u 2 ispravna i vjerojatnost je
=1-*
U tri ispravna ocito nemos doc.
Cekanje u stanje 1 je min{Exp(1/30),Exp(1/2),Exp(1/2)}~Exp(31/30}
tj. dok se jedan ne pokvari ili ostali ne poprave
Zakljucujes lambda(1)=31/30
Napravis tako i za ostala stanja (hint: ocito iz stanja 3 mozes doc samo u stanje 2)
Sada imas matricu prijelaza diskretnog P i funkciju lambda
Napravis generatorsku matricu A i izracunas stacionarnu distribuciju
te ocitas zeljeni rezultat.
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 10:24 sri, 28. 11. 2007 Naslov: Postano: 10:24 sri, 28. 11. 2007 Naslov: |
    |
|
|
[quote="Mr.Doe"]Jos jedan:
Neka [latex](Z_n,n\geq 0)[/latex] proces grananja za koji [latex]Z_0=1,\mathbb{P}(Z_1=k)=pg^k,~k\geq 0,~p+g=1[/latex]. Neka [latex] T=\min\{n:Z_n=0\}[/latex].
(a) Izracunajte [latex]p_n=\mathbb{P}(T=n)[/latex]
(b) Za koje vrijednosti od p je [latex]\mathbb{E}[T]<+\infty[/latex]
Uspio sam naci da je (u (a)) [latex]\displaystyle p_n=\sum_{k=1}^{\infty}pg^k p_{n-1}^k,~n\geq 2[/latex], ali dalje od toga nisam, dosao, te mi ovo ne izgleda obecavajuce.
off-topic: to vsego: jer mozes staviti da za pisanje u LaTex-u koristimo $ - $ switch, jer ove sadasnje switchove je dosta naporno stalno pisati?[/quote]
[latex]P(T=n)=P(\{Z_{n}=0\} \backslash \{Z_{n-1}=0\})=P(Z_{n}=0) - P(Z_{n-1}=0)[/latex]
indukcijom pokazes da je
[latex]P(Z_{n}=0)= \frac{n}{n+1},\ p=q[/latex]
[latex]P(Z_{n}=0)= \frac{p(q^n - p^n)}{q^{n+1} - p^{n+1}},\ p \neq q[/latex]
i tako dobijes P(T=n)
e sad sto se tice E[T]<+oo
to je trivijalno za p=q=1/2 (ne vrijedi)
ali za [latex]p \neq q[/latex] nisam uspio rijesiti
| Mr.Doe (napisa): | Jos jedan:
Neka 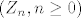 proces grananja za koji proces grananja za koji 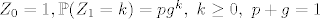 . Neka . Neka 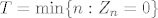 . .
(a) Izracunajte 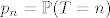
(b) Za koje vrijednosti od p je 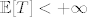
Uspio sam naci da je (u (a)) 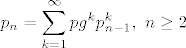 , ali dalje od toga nisam, dosao, te mi ovo ne izgleda obecavajuce. , ali dalje od toga nisam, dosao, te mi ovo ne izgleda obecavajuce.
off-topic: to vsego: jer mozes staviti da za pisanje u LaTex-u koristimo $ - $ switch, jer ove sadasnje switchove je dosta naporno stalno pisati? |
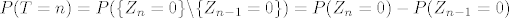
indukcijom pokazes da je
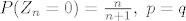
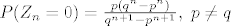
i tako dobijes P(T=n)
e sad sto se tice E[T]<+oo
to je trivijalno za p=q=1/2 (ne vrijedi)
ali za 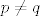 nisam uspio rijesiti nisam uspio rijesiti
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
marijap
Forumaš(ica)


Pridružen/a: 21. 06. 2006. (19:04:40)
Postovi: (209)16
Spol: 
Lokacija: zg
|
 Postano: 15:02 pet, 25. 1. 2008 Naslov: Postano: 15:02 pet, 25. 1. 2008 Naslov: |
    |
|
|
[quote="GauSs_"][quote="Anonymous"]Moze li netko napisati kako izgleda matrica prijelaza za ovaj zadatak:
Jedan kosarkas pogadja svoje suteve sa slijedecim vjerojatnostima:
s vjer. 1/2 ako je promasio posljednja dva suta,
s vjerojatnoscu 2/3 ako je pogodio jedan od svoja dva posljednja suta
i s vjer. 3/4 ako je pogodio oba svoja dva posljednja suta.
Za prostor stanja uzmite S={PP,PU,UP,UU} gdje stanje predstavlja uredjeni par posljednja dva kosarkaseva suta, P-promasaj,U-ubacaj.[/quote]
[latex] P = \left[ \begin{array}{cccc}
1/2 & 1/2 & 0 & 0 \\
0 & 0 & 1/3 & 2/3 \\
1/3 & 2/3 & 0 &0 \\
0 & 0 & 1/4 & 3/4
\end{array} \right] [/latex][/quote]
Stacionarnu distribuciju sam izračunala, ali nisam sigurna za konačni rezultat: Koliki je postotak košarkaševa šuta (ubačaja) nakon dugo vremena? Meni je ispalo 68.7%
| GauSs_ (napisa): | | Anonymous (napisa): | Moze li netko napisati kako izgleda matrica prijelaza za ovaj zadatak:
Jedan kosarkas pogadja svoje suteve sa slijedecim vjerojatnostima:
s vjer. 1/2 ako je promasio posljednja dva suta,
s vjerojatnoscu 2/3 ako je pogodio jedan od svoja dva posljednja suta
i s vjer. 3/4 ako je pogodio oba svoja dva posljednja suta.
Za prostor stanja uzmite S={PP,PU,UP,UU} gdje stanje predstavlja uredjeni par posljednja dva kosarkaseva suta, P-promasaj,U-ubacaj. |
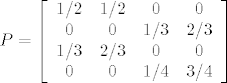 |
Stacionarnu distribuciju sam izračunala, ali nisam sigurna za konačni rezultat: Koliki je postotak košarkaševa šuta (ubačaja) nakon dugo vremena? Meni je ispalo 68.7%
|
|
| [Vrh] |
|
hexy
Forumaš(ica)

Pridružen/a: 19. 11. 2002. (09:39:35)
Postovi: (8A)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 18:08 uto, 26. 2. 2008 Naslov: Postano: 18:08 uto, 26. 2. 2008 Naslov: |
    |
|
|
[quote="GauSs_"][quote="Mr.Doe"]... To je puno jednostavnije. ...[/quote]
ako je jednostavnije objasni nam.
mi tvrdimo (malo modificirao Kobrinu izjavu):
[quote="Kobra&GauSs_"] Ako je zbroj dviju nezavisnih nenegativnih cjelobrojnih sl. varijabli X i Y binomna sl- varijabla s parametrima (n,p) , tada su nužno i X i Y binomne sl. varijable s parametrima (m1,p) odnosno (m2,p) t.d. m1+m2=n. [/quote]
a zadatak kaze:
[quote="Zadatak"] Neka su X i Y nezavisne cjelobrojne nenegativne slucajne varijable takve da je X+Y binomna sa parametrima (n,p). Dokazite da postoje m1,m2 takvi da je m1+m2=n, X je binomna s parametrima (m1,p), a Y binomna s parametrima (m2,p). [/quote]
gdje tocno grijesimo?[/quote]
Znam da je proslo vremena, al cini mi se nigdje. Mislim da je u ovom slucaju Mr.Doe krivo shvatio, odnosno pokazati da postoje m1 i m2 takvi da su X i Y binomne sa danim parametrima je isto kao reci da trebamo pokazati da su binomne.
Kad smo kod toga, i mene taj zadatak muci. :-? Mislim, najelegantnije se cini sa f-jama izvodnicama ali stanem skoro odmah na pocetku bez ideje. I pokazao sam što i ljudi ovdje, da je maksimum koji X postize neki m1<n a Y n-m1, ali dalje...
Ali ovo ne bi smjelo biti nešto preteško, a izgleda da se svi mučimo baš s tim. Ako netko ima ideju ili zna rjesenje, very much appreciated :angel:
| GauSs_ (napisa): | | Mr.Doe (napisa): | | ... To je puno jednostavnije. ... |
ako je jednostavnije objasni nam.
mi tvrdimo (malo modificirao Kobrinu izjavu):
| Kobra&GauSs_ (napisa): | | Ako je zbroj dviju nezavisnih nenegativnih cjelobrojnih sl. varijabli X i Y binomna sl- varijabla s parametrima (n,p) , tada su nužno i X i Y binomne sl. varijable s parametrima (m1,p) odnosno (m2,p) t.d. m1+m2=n. |
a zadatak kaze:
| Zadatak (napisa): | | Neka su X i Y nezavisne cjelobrojne nenegativne slucajne varijable takve da je X+Y binomna sa parametrima (n,p). Dokazite da postoje m1,m2 takvi da je m1+m2=n, X je binomna s parametrima (m1,p), a Y binomna s parametrima (m2,p). |
gdje tocno grijesimo? |
Znam da je proslo vremena, al cini mi se nigdje. Mislim da je u ovom slucaju Mr.Doe krivo shvatio, odnosno pokazati da postoje m1 i m2 takvi da su X i Y binomne sa danim parametrima je isto kao reci da trebamo pokazati da su binomne.
Kad smo kod toga, i mene taj zadatak muci.  Mislim, najelegantnije se cini sa f-jama izvodnicama ali stanem skoro odmah na pocetku bez ideje. I pokazao sam što i ljudi ovdje, da je maksimum koji X postize neki m1<n a Y n-m1, ali dalje... Mislim, najelegantnije se cini sa f-jama izvodnicama ali stanem skoro odmah na pocetku bez ideje. I pokazao sam što i ljudi ovdje, da je maksimum koji X postize neki m1<n a Y n-m1, ali dalje...
Ali ovo ne bi smjelo biti nešto preteško, a izgleda da se svi mučimo baš s tim. Ako netko ima ideju ili zna rjesenje, very much appreciated 
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 18:47 uto, 26. 2. 2008 Naslov: Postano: 18:47 uto, 26. 2. 2008 Naslov: |
    |
|
|
Dakako, postoji mogucnost da sam ja totalno promasio, ali da objasnim u cemu je problem ako zelimo pokazati da su te sl. varijable nuzno binomne ( sa pripadnim parametrima ), dakle mi bi trebali rijesiti ( direktno ) sustav i pokazati da je rjesenje jedinstveno !! (to je ono sto nas muci) ;
[latex]\displaystyle {n \choose k} p^kg^{n-k}=\sum_{i=0}^{k}a_i b_{k-i},~k=0,\dots,n [/latex], gdje je [latex](a_i)_{i=0,\dots n},~(b_i)_{i=0,\dots,n}[/latex] fije gustoce od [latex]X[/latex], odnosno [latex]Y[/latex], a mislim da bas necemo imati previse srece sa time. Dakle, ukoliko netko ima ideju kako pokazati da (nelinearni !!!) sustav ima jedinstveno rjesenje, neka slobodno kaze. Ja i dalje tvrdim da trebamo pokazati da rjesenje postoji, a to sam napisao kako bi to dobili, i onda lagano putem fija izvodnica se vidi da suma sl. varijabli jest binomna.
@vili: kako si dobio ocekivano vrijeme posjeta lanca stanju [latex] \{1,2\}[/latex] ( 3 zad. sa zadnjeg roka ). Sa time se malo mucim. :oops:
Edit: ispricavam se, kada mislim na jedinstveno rjesenje, mislim na to da nema rjesenja van klase binomnih slucajnih varijabli ( tj sva binomna rjesenja sam strpao u "jedan koš" )
Dakako, postoji mogucnost da sam ja totalno promasio, ali da objasnim u cemu je problem ako zelimo pokazati da su te sl. varijable nuzno binomne ( sa pripadnim parametrima ), dakle mi bi trebali rijesiti ( direktno ) sustav i pokazati da je rjesenje jedinstveno !! (to je ono sto nas muci) ;
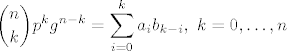 , gdje je , gdje je 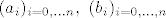 fije gustoce od fije gustoce od  , odnosno , odnosno  , a mislim da bas necemo imati previse srece sa time. Dakle, ukoliko netko ima ideju kako pokazati da (nelinearni !!!) sustav ima jedinstveno rjesenje, neka slobodno kaze. Ja i dalje tvrdim da trebamo pokazati da rjesenje postoji, a to sam napisao kako bi to dobili, i onda lagano putem fija izvodnica se vidi da suma sl. varijabli jest binomna. , a mislim da bas necemo imati previse srece sa time. Dakle, ukoliko netko ima ideju kako pokazati da (nelinearni !!!) sustav ima jedinstveno rjesenje, neka slobodno kaze. Ja i dalje tvrdim da trebamo pokazati da rjesenje postoji, a to sam napisao kako bi to dobili, i onda lagano putem fija izvodnica se vidi da suma sl. varijabli jest binomna.
@vili: kako si dobio ocekivano vrijeme posjeta lanca stanju 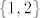 ( 3 zad. sa zadnjeg roka ). Sa time se malo mucim. ( 3 zad. sa zadnjeg roka ). Sa time se malo mucim. 
Edit: ispricavam se, kada mislim na jedinstveno rjesenje, mislim na to da nema rjesenja van klase binomnih slucajnih varijabli ( tj sva binomna rjesenja sam strpao u "jedan koš" )
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 19:50 uto, 26. 2. 2008 Naslov: Postano: 19:50 uto, 26. 2. 2008 Naslov: |
    |
|
|
[quote="Mr.Doe"]Dakako, postoji mogucnost da sam ja totalno promasio, ali da objasnim u cemu je problem ako zelimo pokazati da su te sl. varijable nuzno binomne ( sa pripadnim parametrima ), dakle mi bi trebali rijesiti ( direktno ) sustav i pokazati da je rjesenje jedinstveno !! (to je ono sto nas muci) ;
[latex]\displaystyle {n \choose k} p^kg^{n-k}=\sum_{i=0}^{k}a_i b_{k-i},~k=0,\dots,n [/latex], gdje je [latex](a_i)_{i=0,\dots n},~(b_i)_{i=0,\dots,n}[/latex] fije gustoce od [latex]X[/latex], odnosno [latex]Y[/latex], a mislim da bas necemo imati previse srece sa time. Dakle, ukoliko netko ima ideju kako pokazati da (nelinearni !!!) sustav ima jedinstveno rjesenje, neka slobodno kaze. Ja i dalje tvrdim da trebamo pokazati da rjesenje postoji, a to sam napisao kako bi to dobili, i onda lagano putem fija izvodnica se vidi da suma sl. varijabli jest binomna.
@vili: kako si dobio ocekivano vrijeme posjeta lanca stanju [latex] \{1,2\}[/latex] ( 3 zad. sa zadnjeg roka ). Sa time se malo mucim. :oops:
Edit: ispricavam se, kada mislim na jedinstveno rjesenje, mislim na to da nema rjesenja van klase binomnih slucajnih varijabli ( tj sva binomna rjesenja sam strpao u "jedan koš" )[/quote]
Ali onda bi zadatak bio zadan kao: X i Y nezavisne binomne s tim i tim parametrima, pokaži da je njihova suma binomna sa određenim parametrima.
Ali u medjuvremenu mi je kolega lemon pomogao s rješenjem zadatka :thankyou:
Dakle, f-ja izvodnica od X+Y je [latex]P(s)=(1-p+ps)^n[/latex], što je polinom n-tog stupnja. Uočimo da i funkcije izvodnice od X i Y također moraju biti polinomi stupnja manjeg ili jednakog od n (ili strogo manjeg ako nećemo gledati degenerirane varijable), što znači da polinomi koji su funkcije izvodnice od X i Y moraju biti djelitelji od [latex]P(s)=(1-p+ps)^n=p^n(s+\frac{1-p}{p})^n[/latex] što mogu jedino biti polinomi oblika [latex]P(s)=p^k(s+\frac{1-p}{p})^k[/latex] za neki 0<=k<=n. To slijedi iz toga što su poznate sve nultočke prvog polinoma, pa su mu ovo jedini djelitelji, a polinom koji ga dijeli nužno množimo sa konstantom [latex]p^k[/latex] zbog toga da bi taj polinom uopće bio f-ja izvodnica neke slučajne varijable (tzv. normiranje).
@Mr.Doe: vjerojatno misliš na drugi zadatak. 1 i 2 sam pretvorio u apsorbirajuća stanja, definirao sam g=1 (na {3,4}) i rješavao prema onom teoremu kod apsorpcijskih vjerojatnosti, w=Qw+g. I sad sam jos očekivanje uvjetovao E(A)= E(A|X_0=1)P(X_0=1)+...+E(A|X_0=4)P(X_0=4). Prva dva su jednaka 0, a druga dva 7/3*1/6+5/3*1/3.
To je generalna ideja, može bit i da sam nekaj zeznuo u računu pa javi ak je to slučaj.
| Mr.Doe (napisa): | Dakako, postoji mogucnost da sam ja totalno promasio, ali da objasnim u cemu je problem ako zelimo pokazati da su te sl. varijable nuzno binomne ( sa pripadnim parametrima ), dakle mi bi trebali rijesiti ( direktno ) sustav i pokazati da je rjesenje jedinstveno !! (to je ono sto nas muci) ;
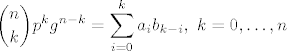 , gdje je , gdje je 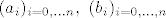 fije gustoce od fije gustoce od  , odnosno , odnosno 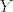 , a mislim da bas necemo imati previse srece sa time. Dakle, ukoliko netko ima ideju kako pokazati da (nelinearni !!!) sustav ima jedinstveno rjesenje, neka slobodno kaze. Ja i dalje tvrdim da trebamo pokazati da rjesenje postoji, a to sam napisao kako bi to dobili, i onda lagano putem fija izvodnica se vidi da suma sl. varijabli jest binomna. , a mislim da bas necemo imati previse srece sa time. Dakle, ukoliko netko ima ideju kako pokazati da (nelinearni !!!) sustav ima jedinstveno rjesenje, neka slobodno kaze. Ja i dalje tvrdim da trebamo pokazati da rjesenje postoji, a to sam napisao kako bi to dobili, i onda lagano putem fija izvodnica se vidi da suma sl. varijabli jest binomna.
@vili: kako si dobio ocekivano vrijeme posjeta lanca stanju 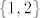 ( 3 zad. sa zadnjeg roka ). Sa time se malo mucim. ( 3 zad. sa zadnjeg roka ). Sa time se malo mucim. 
Edit: ispricavam se, kada mislim na jedinstveno rjesenje, mislim na to da nema rjesenja van klase binomnih slucajnih varijabli ( tj sva binomna rjesenja sam strpao u "jedan koš" ) |
Ali onda bi zadatak bio zadan kao: X i Y nezavisne binomne s tim i tim parametrima, pokaži da je njihova suma binomna sa određenim parametrima.
Ali u medjuvremenu mi je kolega lemon pomogao s rješenjem zadatka 
Dakle, f-ja izvodnica od X+Y je 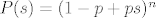 , što je polinom n-tog stupnja. Uočimo da i funkcije izvodnice od X i Y također moraju biti polinomi stupnja manjeg ili jednakog od n (ili strogo manjeg ako nećemo gledati degenerirane varijable), što znači da polinomi koji su funkcije izvodnice od X i Y moraju biti djelitelji od , što je polinom n-tog stupnja. Uočimo da i funkcije izvodnice od X i Y također moraju biti polinomi stupnja manjeg ili jednakog od n (ili strogo manjeg ako nećemo gledati degenerirane varijable), što znači da polinomi koji su funkcije izvodnice od X i Y moraju biti djelitelji od 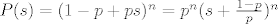 što mogu jedino biti polinomi oblika što mogu jedino biti polinomi oblika 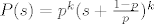 za neki 0⇐k⇐n. To slijedi iz toga što su poznate sve nultočke prvog polinoma, pa su mu ovo jedini djelitelji, a polinom koji ga dijeli nužno množimo sa konstantom za neki 0⇐k⇐n. To slijedi iz toga što su poznate sve nultočke prvog polinoma, pa su mu ovo jedini djelitelji, a polinom koji ga dijeli nužno množimo sa konstantom 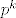 zbog toga da bi taj polinom uopće bio f-ja izvodnica neke slučajne varijable (tzv. normiranje). zbog toga da bi taj polinom uopće bio f-ja izvodnica neke slučajne varijable (tzv. normiranje).
@Mr.Doe: vjerojatno misliš na drugi zadatak. 1 i 2 sam pretvorio u apsorbirajuća stanja, definirao sam g=1 (na {3,4}) i rješavao prema onom teoremu kod apsorpcijskih vjerojatnosti, w=Qw+g. I sad sam jos očekivanje uvjetovao E(A)= E(A|X_0=1)P(X_0=1)+...+E(A|X_0=4)P(X_0=4). Prva dva su jednaka 0, a druga dva 7/3*1/6+5/3*1/3.
To je generalna ideja, može bit i da sam nekaj zeznuo u računu pa javi ak je to slučaj.
|
|
| [Vrh] |
|
|













