| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:40 ned, 25. 11. 2007 Naslov: Dokaz da je nešto potprostor? (postupak) Postano: 19:40 ned, 25. 11. 2007 Naslov: Dokaz da je nešto potprostor? (postupak) |
    |
|
|
Evo, trivijalan primjer. Kako pokazati da je [latex]M=\{(1,0,0),(0,1,0)\} [/latex] potprostor od [latex]V^3[/latex]?
Treba dokazati da su naslijeđene operacije zbrajanja i množenja iz [latex]V^3[/latex]... Tj da je:
[latex]a+b\in M, \forall a, b \in M,[/latex]
[latex]\alpha a \in M, \forall \alpha\in\mathbb{F}, \forall a \in M[/latex]
I kak da sad to napišem?
[latex](1,0,0)+(0,1,0)=(1,1,0) \rightarrow (1,1,0) \in M[/latex]
[latex]\alpha(1,0,0)+\beta(0,1,0)=(\alpha,\beta,0) \rightarrow (\alpha,\beta,0)\in M[/latex]
Ili kako? Je li ovo dovoljan dokaz? Ikakav dokaz :lol: ?
Evo, trivijalan primjer. Kako pokazati da je 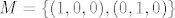 potprostor od potprostor od 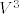 ? ?
Treba dokazati da su naslijeđene operacije zbrajanja i množenja iz 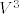 ... Tj da je: ... Tj da je:
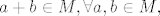
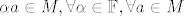
I kak da sad to napišem?
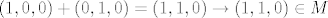
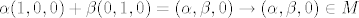
Ili kako? Je li ovo dovoljan dokaz? Ikakav dokaz  ? ?
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 20:44 ned, 25. 11. 2007 Naslov: Postano: 20:44 ned, 25. 11. 2007 Naslov: |
    |
|
|
Mislim da tu trebaš uzet 2 proizvoljna vektora iz M pa pokazat da je njihov zbroj, tj 'produljenje' ('smanjenje') za alfa u M.
Pa uzmeš (x1,y1,0) i (x2,y2,0) i pokažeš da je njihov zbroj u M. To su vektori u V3 pa ih znaš zbrojit pa pokažeš kao lin komb vekt iz baze za M.
Analogno za alfa(x1,y1,0)...
;)
Mislim da tu trebaš uzet 2 proizvoljna vektora iz M pa pokazat da je njihov zbroj, tj 'produljenje' ('smanjenje') za alfa u M.
Pa uzmeš (x1,y1,0) i (x2,y2,0) i pokažeš da je njihov zbroj u M. To su vektori u V3 pa ih znaš zbrojit pa pokažeš kao lin komb vekt iz baze za M.
Analogno za alfa(x1,y1,0)...

_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 3:22 pon, 26. 11. 2007 Naslov: Postano: 3:22 pon, 26. 11. 2007 Naslov: |
    |
|
|
rafaelm, ne vidim u cemu je problem.... Skup ta dva vektora, tj. M, je vektorski prostor, i on je potprostor od V3.
Ili obrnuto, ako dokazemo da je M potprostor vektorskog prostora M, onda je i on sam (M) vektorski prostor.
Nije mi jasno sta si htio reci sa tom linearnom ljuskom??
I cak se vidi po obliku, (1,0,0) i (0,1,0), da ta 2 vektora razapinju V2 u vektorskom prostoru V3...
Explain yourself. 8)
[size=7]p.s. malo sam osjetljiv na izraze kao sto je linearna ljuska [/size]:-s
rafaelm, ne vidim u cemu je problem.... Skup ta dva vektora, tj. M, je vektorski prostor, i on je potprostor od V3.
Ili obrnuto, ako dokazemo da je M potprostor vektorskog prostora M, onda je i on sam (M) vektorski prostor.
Nije mi jasno sta si htio reci sa tom linearnom ljuskom??
I cak se vidi po obliku, (1,0,0) i (0,1,0), da ta 2 vektora razapinju V2 u vektorskom prostoru V3...
Explain yourself. 
p.s. malo sam osjetljiv na izraze kao sto je linearna ljuska 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 4:14 pon, 26. 11. 2007 Naslov: Postano: 4:14 pon, 26. 11. 2007 Naslov: |
    |
|
|
Skup ta dva vektora [b][u]nije[/u][/b] vektorski prostor. :? Npr, za [latex]\alpha=\beta=\frac12[/latex], imamo:
[latex]\alpha a + \beta b = (\frac12, \frac12) \not\in \{a,b\}[/latex]
za [latex]a = (1,0,0)[/latex] i [latex]b = (0,1,0)[/latex].
S druge strane, ljuska je po definiciji vektorski (pot)prostor (definiramo ju kao presjek svih (pot)prostora koji sadrze zadane vektore). ;)
Skup ta dva vektora nije vektorski prostor.  Npr, za Npr, za 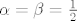 , imamo: , imamo:
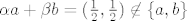
za 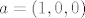 i i 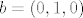 . .
S druge strane, ljuska je po definiciji vektorski (pot)prostor (definiramo ju kao presjek svih (pot)prostora koji sadrze zadane vektore). 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 5:34 pon, 26. 11. 2007 Naslov: Postano: 5:34 pon, 26. 11. 2007 Naslov: |
    |
|
|
[quote="vsego"]Skup ta dva vektora [b][u]nije[/u][/b] vektorski prostor. :? Npr, za [latex]\alpha=\beta=\frac12[/latex], imamo:
[latex]\alpha a + \beta b = (\frac12, \frac12) \not\in \{a,b\}[/latex]
za [latex]a = (1,0,0)[/latex] i [latex]b = (0,1,0)[/latex].
S druge strane, ljuska je po definiciji vektorski (pot)prostor (definiramo ju kao presjek svih (pot)prostora koji sadrze zadane vektore). ;)[/quote]
Sad mi bas nije najjasnije...
xa + yb, x=y=1/2 , x,y skalari (aka alfa i beta :))
xa + yb = 1/2*(1,0,0)+1/2*(0,1,0) = (1/2, 1/2, 0), sto je element od M, tj element od {a, b}
Gdje grijesim? :jutro:
| vsego (napisa): | Skup ta dva vektora nije vektorski prostor.  Npr, za Npr, za 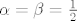 , imamo: , imamo:
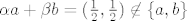
za 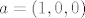 i i 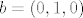 . .
S druge strane, ljuska je po definiciji vektorski (pot)prostor (definiramo ju kao presjek svih (pot)prostora koji sadrze zadane vektore).  |
Sad mi bas nije najjasnije...
xa + yb, x=y=1/2 , x,y skalari (aka alfa i beta  ) )
xa + yb = 1/2*(1,0,0)+1/2*(0,1,0) = (1/2, 1/2, 0), sto je element od M, tj element od {a, b}
Gdje grijesim? 
_________________
Đante tanda fandiga?
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 5:46 pon, 26. 11. 2007 Naslov: Postano: 5:46 pon, 26. 11. 2007 Naslov: |
    |
|
|
Dakle, ti tvrdis:
[latex](\frac12,\frac12,0) \in \lbrace (1,0,0), (0,1,0) \rbrace[/latex] :?: :shock:
Kao da kazes da je
[latex]\frac12 \in \lbrace 0, 1 \rbrace[/latex] :|
[b]Razlikuj skup od ljuske kojem je taj skup baza[/b] :!:
:!: [latex]\lbrace (1,0,0), (0,1,0) \rbrace \not= \[\lbrace (1,0,0), (0,1,0) \rbrace\][/latex] :!:
Lijevo je dvoclani skup, a desno dvodimenzionalni realni prostor... 8)
Dakle, ti tvrdis:
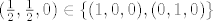  
Kao da kazes da je
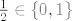 
Razlikuj skup od ljuske kojem je taj skup baza 
 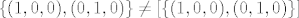 
Lijevo je dvoclani skup, a desno dvodimenzionalni realni prostor... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 6:04 pon, 26. 11. 2007 Naslov: Postano: 6:04 pon, 26. 11. 2007 Naslov: |
    |
|
|
Onda sam i ja krivo pitanje postavio... Pravilno postavljen zadatak bi valjda onda glasio:
Pokažite da je [latex][M]=\{(1,0,0),(0,1,0)\} [/latex] potprostor od [latex]V^3[/latex]
Hmmm... Ako želimo govoriti o linearnoj ljusci od [latex]M=\{(1,0,0),(0,1,0)\} [/latex] , da li se piše
[latex][M]=\{(1,0,0),(0,1,0)\} [/latex]
ili
[latex]M=[\{(1,0,0),(0,1,0)\}][/latex]
ili pak
[latex][M]=[\{(1,0,0),(0,1,0)\}][/latex]
Sad sam malo zbunjen u 6 ujutro...
Bez šale, imam noćne more sad od tih zagrada i nemrem spavat :silly:
Sanjao sam da me Bakić zrušio radi krive zagrade.
[EDIT]
Hmm... Workaround:
Pokažite da je [latex][M][/latex] potprostor od [latex]V^3, M=\{(1,0,0),(0,1,0)\}[/latex]
:skakavci:
Onda sam i ja krivo pitanje postavio... Pravilno postavljen zadatak bi valjda onda glasio:
Pokažite da je 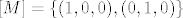 potprostor od potprostor od 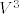
Hmmm... Ako želimo govoriti o linearnoj ljusci od 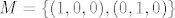 , da li se piše , da li se piše
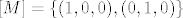
ili
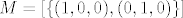
ili pak
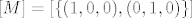
Sad sam malo zbunjen u 6 ujutro...
Bez šale, imam noćne more sad od tih zagrada i nemrem spavat 
Sanjao sam da me Bakić zrušio radi krive zagrade.
[EDIT]
Hmm... Workaround:
Pokažite da je 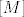 potprostor od potprostor od 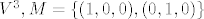

|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 13:50 pon, 26. 11. 2007 Naslov: Postano: 13:50 pon, 26. 11. 2007 Naslov: |
    |
|
|
[quote="punio4"][latex][M]=\{(1,0,0),(0,1,0)\} [/latex][/quote]
Krivo, jer lijevo pise "ljuska od M", a desno uopce nije ljuska (tj. ne postoji M da bi napisano imalo smisla). :)
[quote="punio4"][latex]M=[\{(1,0,0),(0,1,0)\}][/latex][/quote]
Ovo kaze da je M linearna ljuska od {(1,0,0),(0,1,0)}. :)
[quote="punio4"][latex][M]=[\{(1,0,0),(0,1,0)\}][/latex][/quote]
Ovo kaze da je ljuska od M jednaka ljuski od {(1,0,0),(0,1,0)}. :)
To [b]ne znaci[/b] da je M = {(1,0,0),(0,1,0)} :!: Na primjer, u [latex]\mathbb{R}^3[/latex] vrijedi:
[latex][\{(1,2,0),(0,3,0)\}]=[\{(1,0,0),(0,1,0)\}][/latex]
jer skupovi {(1,2,0),(0,3,0)} i {(1,0,0),(0,1,0)} razapinju isti prostor. ;)
[quote="punio4"]Sanjao sam da me Bakić zrušio radi krive zagrade.[/quote]
:lol:
[quote="punio4"]Pokažite da je [latex][M][/latex] potprostor od [latex]V^3, M=\{(1,0,0),(0,1,0)\}[/latex][/quote]
IMO, ovo je tocno ono sto si htio reci u originalnom zadatku. =D>
Samo, tu se malo gubi smisao zadatka jer trazis da se "pokaze da je linearna ljuska potprostor", a linearna ljuska je [b]po definiciji[/b] "presjek svih potprostora (sto znamo da je potprostor) koji sadrze zadani skup", pa se nema sto pokazivati. :?
Recimo, smislenije je:
Pokazite da je skup [latex]S := \{(a,b,0):\ a,b, \in \mathbb{R}\}[/latex] potprostor od [latex]\mathbb{R}^3[/latex]. :) Rijec je o istom skupu o kojem gore pricas, ali nigdje ne pise "ljuska", pa treba ponesto i pokazati (ili da je S ljuska od onog gore M ili direktno da je S stvarno potprostor). 8)
| punio4 (napisa): | 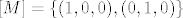 |
Krivo, jer lijevo pise "ljuska od M", a desno uopce nije ljuska (tj. ne postoji M da bi napisano imalo smisla). 
| punio4 (napisa): | 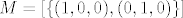 |
Ovo kaze da je M linearna ljuska od {(1,0,0),(0,1,0)}. 
| punio4 (napisa): | 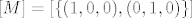 |
Ovo kaze da je ljuska od M jednaka ljuski od {(1,0,0),(0,1,0)}. 
To ne znaci da je M = {(1,0,0),(0,1,0)}  Na primjer, u Na primjer, u 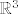 vrijedi: vrijedi:
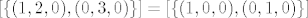
jer skupovi {(1,2,0),(0,3,0)} i {(1,0,0),(0,1,0)} razapinju isti prostor. 
| punio4 (napisa): | | Sanjao sam da me Bakić zrušio radi krive zagrade. |

| punio4 (napisa): | Pokažite da je 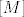 potprostor od potprostor od 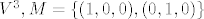 |
IMO, ovo je tocno ono sto si htio reci u originalnom zadatku. 
Samo, tu se malo gubi smisao zadatka jer trazis da se "pokaze da je linearna ljuska potprostor", a linearna ljuska je po definiciji "presjek svih potprostora (sto znamo da je potprostor) koji sadrze zadani skup", pa se nema sto pokazivati. 
Recimo, smislenije je:
Pokazite da je skup 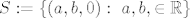 potprostor od potprostor od 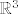 . .  Rijec je o istom skupu o kojem gore pricas, ali nigdje ne pise "ljuska", pa treba ponesto i pokazati (ili da je S ljuska od onog gore M ili direktno da je S stvarno potprostor). Rijec je o istom skupu o kojem gore pricas, ali nigdje ne pise "ljuska", pa treba ponesto i pokazati (ili da je S ljuska od onog gore M ili direktno da je S stvarno potprostor). 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
 Postano: 20:53 uto, 27. 11. 2007 Naslov: Postano: 20:53 uto, 27. 11. 2007 Naslov: |
    |
|
|
ljudi imam zadatak od nekog tamo prije kolokvija
U kompleksnom vektorskom prostoru C^3 zadan je skup
S = {(1,1,i), (i,-1,1), (2i,i-1,0)}
je li skup s sustav izvodnica i baza za C^3?
e budući da ovakav nismo baš radili zapela sam u rješavanju nakon što to sve matrično zapišem i počnem rješavat onaj sustav
ljudi imam zadatak od nekog tamo prije kolokvija
U kompleksnom vektorskom prostoru C^3 zadan je skup
S = {(1,1,i), (i,-1,1), (2i,i-1,0)}
je li skup s sustav izvodnica i baza za C^3?
e budući da ovakav nismo baš radili zapela sam u rješavanju nakon što to sve matrično zapišem i počnem rješavat onaj sustav
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 21:42 uto, 27. 11. 2007 Naslov: Postano: 21:42 uto, 27. 11. 2007 Naslov: |
    |
|
|
[quote="anam"]ljudi imam zadatak od nekog tamo prije kolokvija
U kompleksnom vektorskom prostoru C^3 zadan je skup
S = {(1,1,i), (i,-1,1), (2i,i-1,0)}
je li skup s sustav izvodnica i baza za C^3?
e budući da ovakav nismo baš radili zapela sam u rješavanju nakon što to sve matrično zapišem i počnem rješavat onaj sustav[/quote]
provjeri je li S nezavisan [size=3](hint: jest! :twisted: )[/size]; ako jest, tada je S baza, jer sadrži onoliko vektora kolika je dimenzija prostora. a ako jest baza, tada je sigurno i sistem izvodnica. :D
| anam (napisa): | ljudi imam zadatak od nekog tamo prije kolokvija
U kompleksnom vektorskom prostoru C^3 zadan je skup
S = {(1,1,i), (i,-1,1), (2i,i-1,0)}
je li skup s sustav izvodnica i baza za C^3?
e budući da ovakav nismo baš radili zapela sam u rješavanju nakon što to sve matrično zapišem i počnem rješavat onaj sustav |
provjeri je li S nezavisan (hint: jest!  ); ako jest, tada je S baza, jer sadrži onoliko vektora kolika je dimenzija prostora. a ako jest baza, tada je sigurno i sistem izvodnica. ); ako jest, tada je S baza, jer sadrži onoliko vektora kolika je dimenzija prostora. a ako jest baza, tada je sigurno i sistem izvodnica. 
_________________
ima let u finish
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 21:58 uto, 27. 11. 2007 Naslov: Postano: 21:58 uto, 27. 11. 2007 Naslov: |
    |
|
|
[quote="anam"]provjerila sam neovisnost i ispalo je da nije ovisan, mislim ako sam dobro radila, ono imaginarno je jednako imaginarnom, realno realnom, pa kako je sve jednako nuli onda je linearno neovisan :?:[/quote]
e sad... ne znam kako si radila, ali moraš pazit kod toga. koliko sam shvatio, ti si uzela realne skalare, odnosno gledala C^3 kao vektorski prostor nad R. u tom slučaju, S sigurno nije ni sistem izvodnica ni baza, jer je dimenzija prostora 6, a |S|=3.
no, mislim da se podrazumijeva da je C^3 prostor nad C, jer se napominje da je kompleksni. :wink:
dakle, moraš dobiti nezavisnost vektora iz S, ali pazi kako radiš, jer ti i ovako slučajno može ispasti dobro, no svejedno ne dobiješ bodove.
uzmi skalare iz C. :D
| anam (napisa): | provjerila sam neovisnost i ispalo je da nije ovisan, mislim ako sam dobro radila, ono imaginarno je jednako imaginarnom, realno realnom, pa kako je sve jednako nuli onda je linearno neovisan  |
e sad... ne znam kako si radila, ali moraš pazit kod toga. koliko sam shvatio, ti si uzela realne skalare, odnosno gledala C^3 kao vektorski prostor nad R. u tom slučaju, S sigurno nije ni sistem izvodnica ni baza, jer je dimenzija prostora 6, a |S|=3.
no, mislim da se podrazumijeva da je C^3 prostor nad C, jer se napominje da je kompleksni. 
dakle, moraš dobiti nezavisnost vektora iz S, ali pazi kako radiš, jer ti i ovako slučajno može ispasti dobro, no svejedno ne dobiješ bodove.
uzmi skalare iz C. 
_________________
ima let u finish
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 22:02 uto, 27. 11. 2007 Naslov: Postano: 22:02 uto, 27. 11. 2007 Naslov: |
    |
|
|
[quote="punio4"]Evo jedno pitanje... Ako imam zadatak koji veli da reduciram neki skup vektora do baze, ili da nađem bazu za sumu, presjek...
Umjesto da rješavam "standardno" sustave jednadžbi, ja napišem u obliku matrice i pokušam negdje dobiti nul-retke...
Da li će mi priznati reducirani skup ako sam negdje elementarnim transformacijama ostale vektore [color=blue]pojednostavio[/color] u procesu? Ili moram paziti koji redak je koji originalni vektor, pa na kraju napisati vektore koji su bili dani u originalnom skupu?[/quote]
misliš: [color=blue]promijenio[/color]? :rofl:
ako se traži da [b]određeni[/b] skup reduciraš, onda [b]njega[/b] moraš reducirati, odnosno napisati originalne vektore. :wink:
| punio4 (napisa): | Evo jedno pitanje... Ako imam zadatak koji veli da reduciram neki skup vektora do baze, ili da nađem bazu za sumu, presjek...
Umjesto da rješavam "standardno" sustave jednadžbi, ja napišem u obliku matrice i pokušam negdje dobiti nul-retke...
Da li će mi priznati reducirani skup ako sam negdje elementarnim transformacijama ostale vektore pojednostavio u procesu? Ili moram paziti koji redak je koji originalni vektor, pa na kraju napisati vektore koji su bili dani u originalnom skupu? |
misliš: promijenio? 
ako se traži da određeni skup reduciraš, onda njega moraš reducirati, odnosno napisati originalne vektore. 
_________________
ima let u finish
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
|




















