| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 22:58 uto, 27. 11. 2007 Naslov: Postano: 22:58 uto, 27. 11. 2007 Naslov: |
    |
|
|
[quote="anam"]jel može pitanje kako uopće pronalazimo bazu za presjek, npr.skupova M i L, ne pronalazim nigdje primjerak takvog zadatka, uglavnom smo radili za sumu?[/quote]
ovako:
neka je baza za M, [latex]\{m_1, m_2, ... , m_p\}[/latex], a baza za L, [latex]\{l_1, l_2, ... , l_q\}[/latex]. unija ta dva skupa je sistem izvodnica za M+L. ako je to ujedno i baza za M+L, suma je direktna, pa je baza presjeka [latex]\{0\}[/latex].
ako unija baza od M i L nije baza za M+L, tada ju do baze možemo svesti. :)
neka smo izbacili [latex]X = \{x_1, x_2, ... , x_r\} \subset \{l_1, l_2, ... , l_q\}[/latex], a neka je [latex]Y = \{y_1, y_2, ... , y_s\}[/latex] (r+s=q) ostao u bazi.
svaki od vektora iz X možemo napisati kao linearnu kombinaciju vektora baze za M+L. evo, uzmemo [latex]x_i[/latex]:
[latex]x_i = \sum_{j=1}^{p} \alpha_j m_j + \sum_{j=1}^s \beta_j y_j[/latex].
e sad malo :piggy: ... prvu sumu iz gornje jednakosti nazovimo [latex]a[/latex], drugu [latex]b[/latex].
[latex]a[/latex] je iz M (kao linearna kombinacija vektora [latex]\{m_1, m_2, ... , m_p\}[/latex]), ali i iz L ([latex]a = x_i - b, x_i, b \in L[/latex]). :arrow: [latex]a \in M\cap L[/latex]
ovo je bio izazov. nadam se da nema greške u zapisu. (latex ubija)
| anam (napisa): | | jel može pitanje kako uopće pronalazimo bazu za presjek, npr.skupova M i L, ne pronalazim nigdje primjerak takvog zadatka, uglavnom smo radili za sumu? |
ovako:
neka je baza za M, 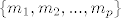 , a baza za L, , a baza za L, 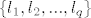 . unija ta dva skupa je sistem izvodnica za M+L. ako je to ujedno i baza za M+L, suma je direktna, pa je baza presjeka . unija ta dva skupa je sistem izvodnica za M+L. ako je to ujedno i baza za M+L, suma je direktna, pa je baza presjeka 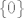 . .
ako unija baza od M i L nije baza za M+L, tada ju do baze možemo svesti. 
neka smo izbacili 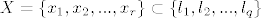 , a neka je , a neka je 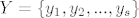 (r+s=q) ostao u bazi. (r+s=q) ostao u bazi.
svaki od vektora iz X možemo napisati kao linearnu kombinaciju vektora baze za M+L. evo, uzmemo 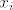 : :
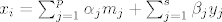 . .
e sad malo  ... prvu sumu iz gornje jednakosti nazovimo ... prvu sumu iz gornje jednakosti nazovimo  , drugu , drugu 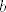 . .
 je iz M (kao linearna kombinacija vektora je iz M (kao linearna kombinacija vektora 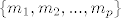 ), ali i iz L ( ), ali i iz L (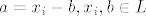 ). ).  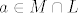
ovo je bio izazov. nadam se da nema greške u zapisu. (latex ubija)
_________________
ima let u finish
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:24 uto, 27. 11. 2007 Naslov: Postano: 23:24 uto, 27. 11. 2007 Naslov: |
    |
|
|
Ok... Ajmo zdravoseljački:
Imaš 2 skupa, [latex]M[/latex] i [latex]L[/latex] koji su reducirani oba do baze, i recimo da je [latex]dimM=2[/latex], a [latex]dimL=3[/latex]
E sad. Zbroj baza je 5. No to ne znači da su međusobno nezavisni (možda se križaju negdje prostori), pa je [latex]dim(M+L)[/latex] takva, da uzmeš svih 5 vektora i njih reduciraš do baze. I recimo dobiješ da je [latex]dim(M+L)=3[/latex], što znači da su 2 vektora neka bila linearno zavisna, tj da je presjek skupova ploha.
E sad... Ako me logika dobro služi:
Imaš prostor dimenzije 3, i kroz njega prolazi neki prostor dimenzije 2...
Presjek njih je ploha, kojima je baza upravo ova 2 vektora koja sam izbacio iz (M+L)
Sam fulao gdje?
Ok... Ajmo zdravoseljački:
Imaš 2 skupa,  i i  koji su reducirani oba do baze, i recimo da je koji su reducirani oba do baze, i recimo da je 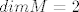 , a , a 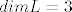
E sad. Zbroj baza je 5. No to ne znači da su međusobno nezavisni (možda se križaju negdje prostori), pa je 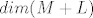 takva, da uzmeš svih 5 vektora i njih reduciraš do baze. I recimo dobiješ da je takva, da uzmeš svih 5 vektora i njih reduciraš do baze. I recimo dobiješ da je 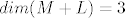 , što znači da su 2 vektora neka bila linearno zavisna, tj da je presjek skupova ploha. , što znači da su 2 vektora neka bila linearno zavisna, tj da je presjek skupova ploha.
E sad... Ako me logika dobro služi:
Imaš prostor dimenzije 3, i kroz njega prolazi neki prostor dimenzije 2...
Presjek njih je ploha, kojima je baza upravo ova 2 vektora koja sam izbacio iz (M+L)
Sam fulao gdje?
Zadnja promjena: punio4; 23:30 uto, 27. 11. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 23:28 uto, 27. 11. 2007 Naslov: Postano: 23:28 uto, 27. 11. 2007 Naslov: |
    |
|
|
Ajd da ja probam zdravo seljački,na primjeru...
neka je [latex]M=[\{(1,0,0),(0,1,0)\}][/latex] i [latex]L=[\{(1,1,0),(0,0,1)\}][/latex]
Sad je [latex][\{(1,0,0),(0,1,0),(1,1,0),(0,0,1)\}][/latex] skup izvodnica za M+L. Taj skup nije linearno nezavisan (vidi se da je (1,1,0)=(1,0,0)+(0,1,0) ) pa izbacimo (1,1,0) iz tog skupa da dobijemo bazu za M+L. Onaj vektor kojeg smo izbacili je baza za MpresjekL prema onom kaj je ma napisao, da se sad ne ponavljam.
edit: nije za smetnut s uma:
[latex]dim(M+L)=dimM+dimL-dim(M \cap L)[/latex]
Ajd da ja probam zdravo seljački,na primjeru...
neka je 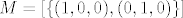 i i 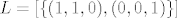
Sad je 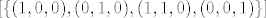 skup izvodnica za M+L. Taj skup nije linearno nezavisan (vidi se da je (1,1,0)=(1,0,0)+(0,1,0) ) pa izbacimo (1,1,0) iz tog skupa da dobijemo bazu za M+L. Onaj vektor kojeg smo izbacili je baza za MpresjekL prema onom kaj je ma napisao, da se sad ne ponavljam. skup izvodnica za M+L. Taj skup nije linearno nezavisan (vidi se da je (1,1,0)=(1,0,0)+(0,1,0) ) pa izbacimo (1,1,0) iz tog skupa da dobijemo bazu za M+L. Onaj vektor kojeg smo izbacili je baza za MpresjekL prema onom kaj je ma napisao, da se sad ne ponavljam.
edit: nije za smetnut s uma:
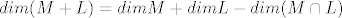
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy 
Zadnja promjena: Luuka; 23:34 uto, 27. 11. 2007; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
 Postano: 0:10 sri, 28. 11. 2007 Naslov: Postano: 0:10 sri, 28. 11. 2007 Naslov: |
    |
|
|
[quote="Masiela"]Znači li to da je baza od presjeka ono što sam izbacila kad sam tražila bazu od L+M?[/quote]
pa i nije baš... ne da mi se smišljat konkretni primjer, pa ajmo ovak... recimo da ti bazu od L čine a1 i a2, a bazu od M b1, b2 i b3... i sad ideš prikazivat b1 pomoću a1 i a2... recimo da to možeš, s koef. alfa1 i alfa2, dakle b1 moraš izbacit van jer nisu lin. nezavisni... sad dalje... uzmeš b2, ideš ga prikazivat pomoću a1 i a2 opet... recimo da to ne ide, dakle lin. nezavisni su, pa ostavljaš b2 u skupu... sad b3 prikazuješ pomoću a1, a2 i b2... recimo da možeš, s koef. beta1, beta2 i beta3... dakle, i b3 mora van... u skupu su ti ostali a1, a2 i b2, oni su baza za L+M... i sad gledaš vektore koji su izbačeni... b1 je prikazan samo pomoću a1 i a2, pa kao takav ide u bazu za presjek ( b1 je očito u M, a kak je prikazan pomoću a1 i a2, on je i u L, pa je i u presjeku)... sad gledaš b3... e njega ne stavljaš 'cijelog' u bazu za presjek, nego samo onaj dio uz a1 i a2, dakle u presjek ide beta1*a1+beta2*a2 ( kad bolje pogledaš, to ti je logično, jer iz prikaza dobiješ da je beta1*a1+beta2*a2= b3-beta3*b2... ovo s lijeve strane ti je iz L, s desne iz M, a to je jednako, pa je očito taj vektor beta1*a1+beta2*a2 u presjeku skupova L i M)... i to ti je onda drugi element baze za presjek... analogno se radi općenito :)
nadam se da je jasno... probaj na konkretnom primjeru iz prošlogodišnjeg kolokvija... sorry na ružnom pisanju oznaka, i ak sam nešto slučajno zeznula :)
| Masiela (napisa): | | Znači li to da je baza od presjeka ono što sam izbacila kad sam tražila bazu od L+M? |
pa i nije baš... ne da mi se smišljat konkretni primjer, pa ajmo ovak... recimo da ti bazu od L čine a1 i a2, a bazu od M b1, b2 i b3... i sad ideš prikazivat b1 pomoću a1 i a2... recimo da to možeš, s koef. alfa1 i alfa2, dakle b1 moraš izbacit van jer nisu lin. nezavisni... sad dalje... uzmeš b2, ideš ga prikazivat pomoću a1 i a2 opet... recimo da to ne ide, dakle lin. nezavisni su, pa ostavljaš b2 u skupu... sad b3 prikazuješ pomoću a1, a2 i b2... recimo da možeš, s koef. beta1, beta2 i beta3... dakle, i b3 mora van... u skupu su ti ostali a1, a2 i b2, oni su baza za L+M... i sad gledaš vektore koji su izbačeni... b1 je prikazan samo pomoću a1 i a2, pa kao takav ide u bazu za presjek ( b1 je očito u M, a kak je prikazan pomoću a1 i a2, on je i u L, pa je i u presjeku)... sad gledaš b3... e njega ne stavljaš 'cijelog' u bazu za presjek, nego samo onaj dio uz a1 i a2, dakle u presjek ide beta1*a1+beta2*a2 ( kad bolje pogledaš, to ti je logično, jer iz prikaza dobiješ da je beta1*a1+beta2*a2= b3-beta3*b2... ovo s lijeve strane ti je iz L, s desne iz M, a to je jednako, pa je očito taj vektor beta1*a1+beta2*a2 u presjeku skupova L i M)... i to ti je onda drugi element baze za presjek... analogno se radi općenito 
nadam se da je jasno... probaj na konkretnom primjeru iz prošlogodišnjeg kolokvija... sorry na ružnom pisanju oznaka, i ak sam nešto slučajno zeznula 
_________________ kalendar 
  |
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 0:19 sri, 28. 11. 2007 Naslov: Postano: 0:19 sri, 28. 11. 2007 Naslov: |
    |
|
|
Kako ne?
Ako imamo neka 2 prostora koji se sjeku, i recimo da su oba dimenzije 3, a da je dimenzija sume isto 3... Dakle imamo 3 vektora koja smo izbacili iz sume.
Ta 3 vektora su nužno linearno nezavisna, i čine bazu za presjek...
E sad, ovo nisam siguran dal su nužno nezavisni, al ak nisu, pa i njih ćemo reducirat do baze, pa opet čine bazu za presjek.
Mislim, čisto vizualno gledajući... Ako postoji:
Presjek prostora dim 2 i 3 je prostor dimenzije 2 (ploha). Presjek dim 2 i 2 je dim 1 (pravac). Presjek prostora dim 3 i 3 je opet 3.
A vektori koji su u oba prostora su očito linearno zavisni, a te smo već izbacili....
Kako ne?
Ako imamo neka 2 prostora koji se sjeku, i recimo da su oba dimenzije 3, a da je dimenzija sume isto 3... Dakle imamo 3 vektora koja smo izbacili iz sume.
Ta 3 vektora su nužno linearno nezavisna, i čine bazu za presjek...
E sad, ovo nisam siguran dal su nužno nezavisni, al ak nisu, pa i njih ćemo reducirat do baze, pa opet čine bazu za presjek.
Mislim, čisto vizualno gledajući... Ako postoji:
Presjek prostora dim 2 i 3 je prostor dimenzije 2 (ploha). Presjek dim 2 i 2 je dim 1 (pravac). Presjek prostora dim 3 i 3 je opet 3.
A vektori koji su u oba prostora su očito linearno zavisni, a te smo već izbacili....
Zadnja promjena: punio4; 0:27 sri, 28. 11. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
 Postano: 0:27 sri, 28. 11. 2007 Naslov: Postano: 0:27 sri, 28. 11. 2007 Naslov: |
    |
|
|
Stavila ovo objašnjenje na papir pa da velim kako sam ga shvatila.
Znači, imam L i M. Imam bazu od L+M, i recimo da tu bazu čini baza od L i dio baze od M.
Sad gledam što mi nije upalo u tu bazu. Raspišem tako da na jednoj strani imam ono što je u L, a na drugoj ono što je u M, i onaj dio koji je u M ide u presjek.
?
Stavila ovo objašnjenje na papir pa da velim kako sam ga shvatila.
Znači, imam L i M. Imam bazu od L+M, i recimo da tu bazu čini baza od L i dio baze od M.
Sad gledam što mi nije upalo u tu bazu. Raspišem tako da na jednoj strani imam ono što je u L, a na drugoj ono što je u M, i onaj dio koji je u M ide u presjek.
?
_________________ mladac: e.k.s. je možda 8%, moje znanje ni toliko  |
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
 Postano: 0:47 sri, 28. 11. 2007 Naslov: Postano: 0:47 sri, 28. 11. 2007 Naslov: |
    |
|
|
ne kužim baš što točno želiš reć :)
dakle... dobiješ bazu za L+M, to je valjda svima jasno kako :) e sad, gledaš one vektore iz M koje si izbacivala... njih si zapisala kao lin. komb. elemenata iz L i iz M... i sad ti u presjek ulazi samo onaj dio uz vektore iz L... jer kad prebaciš onaj dio koji je uz vektore iz M na drugu stranu, na lijevoj strani bit će ti nešto iz L, na desnoj iz M, kak je to jednako, bit će iz presjeka, a lijeva strana je upravo gore spomenuti dio uz vektore iz L...
jasnije? :) makar se ne bi čudila da nije, baš sam sve spetljala sada :D
ne kužim baš što točno želiš reć 
dakle... dobiješ bazu za L+M, to je valjda svima jasno kako  e sad, gledaš one vektore iz M koje si izbacivala... njih si zapisala kao lin. komb. elemenata iz L i iz M... i sad ti u presjek ulazi samo onaj dio uz vektore iz L... jer kad prebaciš onaj dio koji je uz vektore iz M na drugu stranu, na lijevoj strani bit će ti nešto iz L, na desnoj iz M, kak je to jednako, bit će iz presjeka, a lijeva strana je upravo gore spomenuti dio uz vektore iz L... e sad, gledaš one vektore iz M koje si izbacivala... njih si zapisala kao lin. komb. elemenata iz L i iz M... i sad ti u presjek ulazi samo onaj dio uz vektore iz L... jer kad prebaciš onaj dio koji je uz vektore iz M na drugu stranu, na lijevoj strani bit će ti nešto iz L, na desnoj iz M, kak je to jednako, bit će iz presjeka, a lijeva strana je upravo gore spomenuti dio uz vektore iz L...
jasnije?  makar se ne bi čudila da nije, baš sam sve spetljala sada makar se ne bi čudila da nije, baš sam sve spetljala sada 
_________________ kalendar 
  |
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
 Postano: 7:26 sri, 28. 11. 2007 Naslov: Postano: 7:26 sri, 28. 11. 2007 Naslov: |
    |
|
|
[quote="arya"]ne kužim baš što točno želiš reć :)
dakle... dobiješ bazu za L+M, to je valjda svima jasno kako :) e sad, gledaš one vektore iz M koje si izbacivala... njih si zapisala kao lin. komb. elemenata iz L i iz M... i sad ti u presjek ulazi samo onaj dio uz vektore iz L... jer kad prebaciš onaj dio koji je uz vektore iz M na drugu stranu, na lijevoj strani bit će ti nešto iz L, na desnoj iz M, kak je to jednako, bit će iz presjeka, a lijeva strana je upravo gore spomenuti dio uz vektore iz L...
jasnije? :) makar se ne bi čudila da nije, baš sam sve spetljala sada :D[/quote]
Napisala sam šturo, čisto štreberski ko neki recept :mrgreen:
Uglavnom, ako imam b3-ß3b2=ß1a1+ß2a2 gdje su a1 i a2 vektori koji su mi u bazi od L+M, shvatila sam da trebam izračunati koliko je b3-ß3b2 i taj rezultat da ide u bazu od presjeka.
| arya (napisa): | ne kužim baš što točno želiš reć 
dakle... dobiješ bazu za L+M, to je valjda svima jasno kako  e sad, gledaš one vektore iz M koje si izbacivala... njih si zapisala kao lin. komb. elemenata iz L i iz M... i sad ti u presjek ulazi samo onaj dio uz vektore iz L... jer kad prebaciš onaj dio koji je uz vektore iz M na drugu stranu, na lijevoj strani bit će ti nešto iz L, na desnoj iz M, kak je to jednako, bit će iz presjeka, a lijeva strana je upravo gore spomenuti dio uz vektore iz L... e sad, gledaš one vektore iz M koje si izbacivala... njih si zapisala kao lin. komb. elemenata iz L i iz M... i sad ti u presjek ulazi samo onaj dio uz vektore iz L... jer kad prebaciš onaj dio koji je uz vektore iz M na drugu stranu, na lijevoj strani bit će ti nešto iz L, na desnoj iz M, kak je to jednako, bit će iz presjeka, a lijeva strana je upravo gore spomenuti dio uz vektore iz L...
jasnije?  makar se ne bi čudila da nije, baš sam sve spetljala sada makar se ne bi čudila da nije, baš sam sve spetljala sada  |
Napisala sam šturo, čisto štreberski ko neki recept 
Uglavnom, ako imam b3-ß3b2=ß1a1+ß2a2 gdje su a1 i a2 vektori koji su mi u bazi od L+M, shvatila sam da trebam izračunati koliko je b3-ß3b2 i taj rezultat da ide u bazu od presjeka.
_________________ mladac: e.k.s. je možda 8%, moje znanje ni toliko  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 9:22 sri, 28. 11. 2007 Naslov: Postano: 9:22 sri, 28. 11. 2007 Naslov: |
    |
|
|
mislio sam da je moj zadnji post koliko-toliko jasan... ljudi, zašto izbjegavate demonstrature :?: :roll:
punio4, ovo shvati samo kao dobronamjeran savjet: moraš malo pripraziti na izražavanje/terminologiju, jer to hoće uzet bodove... :wink:
[quote="punio4"]Ok... Ajmo zdravoseljački:
Imaš 2 skupa, [latex]M[/latex] i [latex]L[/latex] koji su reducirani oba do baze, i recimo da je [latex]dimM=2[/latex], a [latex]dimL=3[/latex][/quote]
ako su M i L [b]skupovi reducirani do baza[/b], onda ne možemo pričati o njihovim dimenzijama, već o dimenzijama njihovih ljusaka.
ako su to, pak, [b]potprostori[/b] (u tvom slučaju dimenzija 2 i 3), onda ih ne svodimo do baze. do baze svodimo sisteme izvodnica ili nadopunjavamo linearno nezavisne skupove (naravno, ukoliko baze već nisu). :wink:
[quote="punio4"]E sad. Zbroj baza je 5. No to ne znači da su međusobno nezavisni (možda se križaju negdje prostori), pa je [latex]dim(M+L)[/latex] takva, da uzmeš svih 5 vektora i njih reduciraš do baze. I recimo dobiješ da je [latex]dim(M+L)=3[/latex], što znači da su 2 vektora neka bila linearno zavisna, tj da je presjek skupova ploha.
E sad... Ako me logika dobro služi:
Imaš prostor dimenzije 3, i kroz njega prolazi neki prostor dimenzije 2...
Presjek njih je ploha, kojima je baza upravo ova 2 vektora koja sam izbacio iz (M+L)[/quote]
pazi, nije sve tako jednostavno. tu pričamo o minimalno petodimenzionalnom prostoru. sve je to lijepo dok si možeš vizualizirati prostor i ravninu i pravac, ali ne valja uvijek tim putem...
tko ti tu garantira da se rečeni prostori dimenzije 3 i dimenzije 2 uopće sijeku? :roll:
[quote="punio4"]Ako imamo neka 2 prostora koji se sjeku, i recimo da su oba dimenzije 3, a da je dimenzija sume isto 3... Dakle imamo 3 vektora koja smo izbacili iz sume. [/quote]
ako su oba potprostora dimenzije 3, a dimenzije 3 je i suma, znači da su ti potprostori jednaki. iz unije baza izbacio si sve vektore baze drugog potprostora (ako si ih lijepo po redu posložio :) ). dimenzija presjeka je 3 (ne, baza nisu izbačeni vektori :!: ), pa je presjek opet taj potprostor. :wink:
[quote="punio4"]Ta 3 vektora su nužno linearno nezavisna, i čine bazu za presjek... [/quote]
NE :!: pročitaj objašnjenja gore.
[quote="punio4"]Mislim, čisto vizualno gledajući... Ako postoji:
Presjek prostora dim 2 i 3 je prostor dimenzije 2 (ploha). Presjek dim 2 i 2 je dim 1 (pravac). Presjek prostora dim 3 i 3 je opet 3. [/quote]
ne. što ako su to potprostori vektorskog prostora [latex]\mathbb{R}^{65}[/latex]? 8) uopće se ne moraju sijeći.
mislio sam da je moj zadnji post koliko-toliko jasan... ljudi, zašto izbjegavate demonstrature  
punio4, ovo shvati samo kao dobronamjeran savjet: moraš malo pripraziti na izražavanje/terminologiju, jer to hoće uzet bodove... 
| punio4 (napisa): | Ok... Ajmo zdravoseljački:
Imaš 2 skupa,  i i  koji su reducirani oba do baze, i recimo da je koji su reducirani oba do baze, i recimo da je 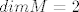 , a , a 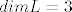 |
ako su M i L skupovi reducirani do baza, onda ne možemo pričati o njihovim dimenzijama, već o dimenzijama njihovih ljusaka.
ako su to, pak, potprostori (u tvom slučaju dimenzija 2 i 3), onda ih ne svodimo do baze. do baze svodimo sisteme izvodnica ili nadopunjavamo linearno nezavisne skupove (naravno, ukoliko baze već nisu). 
| punio4 (napisa): | E sad. Zbroj baza je 5. No to ne znači da su međusobno nezavisni (možda se križaju negdje prostori), pa je 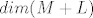 takva, da uzmeš svih 5 vektora i njih reduciraš do baze. I recimo dobiješ da je takva, da uzmeš svih 5 vektora i njih reduciraš do baze. I recimo dobiješ da je 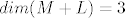 , što znači da su 2 vektora neka bila linearno zavisna, tj da je presjek skupova ploha. , što znači da su 2 vektora neka bila linearno zavisna, tj da je presjek skupova ploha.
E sad... Ako me logika dobro služi:
Imaš prostor dimenzije 3, i kroz njega prolazi neki prostor dimenzije 2...
Presjek njih je ploha, kojima je baza upravo ova 2 vektora koja sam izbacio iz (M+L) |
pazi, nije sve tako jednostavno. tu pričamo o minimalno petodimenzionalnom prostoru. sve je to lijepo dok si možeš vizualizirati prostor i ravninu i pravac, ali ne valja uvijek tim putem...
tko ti tu garantira da se rečeni prostori dimenzije 3 i dimenzije 2 uopće sijeku? 
| punio4 (napisa): | | Ako imamo neka 2 prostora koji se sjeku, i recimo da su oba dimenzije 3, a da je dimenzija sume isto 3... Dakle imamo 3 vektora koja smo izbacili iz sume. |
ako su oba potprostora dimenzije 3, a dimenzije 3 je i suma, znači da su ti potprostori jednaki. iz unije baza izbacio si sve vektore baze drugog potprostora (ako si ih lijepo po redu posložio  ). dimenzija presjeka je 3 (ne, baza nisu izbačeni vektori ). dimenzija presjeka je 3 (ne, baza nisu izbačeni vektori  ), pa je presjek opet taj potprostor. ), pa je presjek opet taj potprostor. 
| punio4 (napisa): | | Ta 3 vektora su nužno linearno nezavisna, i čine bazu za presjek... |
NE  pročitaj objašnjenja gore. pročitaj objašnjenja gore.
| punio4 (napisa): | Mislim, čisto vizualno gledajući... Ako postoji:
Presjek prostora dim 2 i 3 je prostor dimenzije 2 (ploha). Presjek dim 2 i 2 je dim 1 (pravac). Presjek prostora dim 3 i 3 je opet 3. |
ne. što ako su to potprostori vektorskog prostora 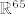 ? ?  uopće se ne moraju sijeći. uopće se ne moraju sijeći.
_________________
ima let u finish
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
 Postano: 10:10 sri, 28. 11. 2007 Naslov: Postano: 10:10 sri, 28. 11. 2007 Naslov: |
    |
|
|
Da doista nismo napravili nijedan takav zadatak al mislim da sam skužila, hvala ljudi na objašnjenju, no pronalazim još jedan tip zadatka koji nismo radili a vidim da je nekad bio u kolokviju
U vektorskom prostoru V nad poljem F za vektore v1, v2,....,vn € V i skalare ß1, ß1,.....ßn € F definiramo vektor
b= ß1v1+ß2b2+......+ßnvn
Ako je skup {v1, v2, ....., vn} linearno nezavisan odredite nužne i dovoljne uvjete na skalare ß1,ß2,.......,ßn tako da i skup {b,v2,v3,....,vn} bude linearno nezavisan :?: :roll:
Da doista nismo napravili nijedan takav zadatak al mislim da sam skužila, hvala ljudi na objašnjenju, no pronalazim još jedan tip zadatka koji nismo radili a vidim da je nekad bio u kolokviju
U vektorskom prostoru V nad poljem F za vektore v1, v2,....,vn € V i skalare ß1, ß1,.....ßn € F definiramo vektor
b= ß1v1+ß2b2+......+ßnvn
Ako je skup {v1, v2, ....., vn} linearno nezavisan odredite nužne i dovoljne uvjete na skalare ß1,ß2,.......,ßn tako da i skup {b,v2,v3,....,vn} bude linearno nezavisan  
|
|
| [Vrh] |
|
Gost
|
 Postano: 13:12 sri, 28. 11. 2007 Naslov: Postano: 13:12 sri, 28. 11. 2007 Naslov: |
    |
|
|
Odgovor: Ako je ß1 = 0, očito je skup linearno zavisan. Dakle, nužno je da ß1 bude različit od 0 da bi skup bio linearno nezavisan. No, je li to i dovoljno? Jest. Možemo skup gledati u poretku vektora {v2,v3,....,vn, b}.
Kako je {v2,v3,....,vn} linearno nezavisan, niti jedan od vektora
v2,v3,....,vn ne može se prikazati pomoću prethodnih pa će
{v2,v3,....,vn, b} biti linearno zavisan ako i samo ako se b može prikazati
pomoću prethodnih vektora. Ako napišemo takav prikaz, nakon malo sređivanja lako dobijemo da se tada i ß1v1 može prikazati pomoću
v2,v3,....,vn, a onda dijeljenjem s ß1 ("množenjem s inverzom", točnije) mogli bismo i v1 prikazati pomoću v2,v3,....,vn, suprotno pretpostavci.
Možemo i formalno, po definiciji, načiniti lin. kombinaciju b,v2,v3,....,vn s nekim koeficijentima i izjednačiti s nulvektorom pa onda nakon malo sređivanja i promatranja koeficijenata vidimo da je ß1 = 0 jedini način da skup {b,v2,v3,....,vn} bude linearno zavisan.
Odgovor: Ako je ß1 = 0, očito je skup linearno zavisan. Dakle, nužno je da ß1 bude različit od 0 da bi skup bio linearno nezavisan. No, je li to i dovoljno? Jest. Možemo skup gledati u poretku vektora {v2,v3,....,vn, b}.
Kako je {v2,v3,....,vn} linearno nezavisan, niti jedan od vektora
v2,v3,....,vn ne može se prikazati pomoću prethodnih pa će
{v2,v3,....,vn, b} biti linearno zavisan ako i samo ako se b može prikazati
pomoću prethodnih vektora. Ako napišemo takav prikaz, nakon malo sređivanja lako dobijemo da se tada i ß1v1 može prikazati pomoću
v2,v3,....,vn, a onda dijeljenjem s ß1 ("množenjem s inverzom", točnije) mogli bismo i v1 prikazati pomoću v2,v3,....,vn, suprotno pretpostavci.
Možemo i formalno, po definiciji, načiniti lin. kombinaciju b,v2,v3,....,vn s nekim koeficijentima i izjednačiti s nulvektorom pa onda nakon malo sređivanja i promatranja koeficijenata vidimo da je ß1 = 0 jedini način da skup {b,v2,v3,....,vn} bude linearno zavisan.
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
 Postano: 14:14 sri, 28. 11. 2007 Naslov: Iz prošlogodišnjeg kolokvija Postano: 14:14 sri, 28. 11. 2007 Naslov: Iz prošlogodišnjeg kolokvija |
    |
|
|
Zadan je skup M={(z1, z2, z3) € C^3: 2z1-z2+2z3=0}.
E sad, kad gledam da li je potprostor i tražim mu neku bazu, da li z1 promatram samo kao z1 ili kao x1+iy1?
Zadan je skup M={(z1, z2, z3) € C^3: 2z1-z2+2z3=0}.
E sad, kad gledam da li je potprostor i tražim mu neku bazu, da li z1 promatram samo kao z1 ili kao x1+iy1?
_________________ mladac: e.k.s. je možda 8%, moje znanje ni toliko  |
|
| [Vrh] |
|
Janie
Forumaš(ica)

Pridružen/a: 28. 11. 2007. (12:12:05)
Postovi: (11)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
|





















