| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
 Postano: 15:04 sri, 28. 11. 2007 Naslov: Postano: 15:04 sri, 28. 11. 2007 Naslov: |
    |
|
|
Samo piše C^3. Znači gledam kao kompeksne?
A kad imam skup s matricama, npr. {[1 1//1 1], [i i//i 0]} (primjer iz zadaće grupe A-N) promatrano u M2(C), kako ga dopuniti do baze?
Ja bi tu recimo za neku bazu uzela {[1 0//0 0], [0 1// 0 0], [0 0// 1 0], [0 0//0 1]} ili tu šemu gdje su umjesto jedinica i-evi. I onda uniju sa {[1 1//1 1], [i i//i 0]} reducirala do baze.
Ali, je l` dobro to što bi ja uzela za bazu od M2(C)? :oops:
Samo piše C^3. Znači gledam kao kompeksne?
A kad imam skup s matricama, npr. {[1 1//1 1], [i i//i 0]} (primjer iz zadaće grupe A-N) promatrano u M2(C), kako ga dopuniti do baze?
Ja bi tu recimo za neku bazu uzela {[1 0//0 0], [0 1// 0 0], [0 0// 1 0], [0 0//0 1]} ili tu šemu gdje su umjesto jedinica i-evi. I onda uniju sa {[1 1//1 1], [i i//i 0]} reducirala do baze.
Ali, je l` dobro to što bi ja uzela za bazu od M2(C)? 
_________________ mladac: e.k.s. je možda 8%, moje znanje ni toliko  |
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 15:09 sri, 28. 11. 2007 Naslov: Postano: 15:09 sri, 28. 11. 2007 Naslov: |
    |
|
|
Dobro bi uzela, znaci skup {M1, M2, E1, E2, E3, E4}
gdje je M1, M2 tvoje dvije matrice-poznate vec
gdje je E1, ..., E4 matrice koje na mjestu 11, 12, 21 i 22 imaju 1, sve ostalo nule.
I da, onda redukcija dok ne dodjes do 4 matrice.
Svejedno ti je da li uzimas sa jedinicama ili i-ovima te matrice(E1...) jer npr. kad bi uzela sa jedinicama ti i dalje mozes opisat cijeli M2(C) jer alfa, beta, gama, delta su elementi od C <--> tj. skalari su iz C, ak me kuzis. 8)
p.s. al ti radje uzmi sa jedinicama te matrice koje ti cine bazu za M2(C) jer je lakse racunat bez i-ova :)
p.s.s. ako bi npr trebala naci bazu za M2(C) nad R, onda ti treba 8 matrica, 4 sa jedinicama, 4 sa i-ovima, tj. E1, E2, E3, E4, Ei11, Ei12, Ei21, Ei22. Jer je dim tog prostora 8.
Dobro bi uzela, znaci skup {M1, M2, E1, E2, E3, E4}
gdje je M1, M2 tvoje dvije matrice-poznate vec
gdje je E1, ..., E4 matrice koje na mjestu 11, 12, 21 i 22 imaju 1, sve ostalo nule.
I da, onda redukcija dok ne dodjes do 4 matrice.
Svejedno ti je da li uzimas sa jedinicama ili i-ovima te matrice(E1...) jer npr. kad bi uzela sa jedinicama ti i dalje mozes opisat cijeli M2(C) jer alfa, beta, gama, delta su elementi od C <--> tj. skalari su iz C, ak me kuzis. 
p.s. al ti radje uzmi sa jedinicama te matrice koje ti cine bazu za M2(C) jer je lakse racunat bez i-ova 
p.s.s. ako bi npr trebala naci bazu za M2(C) nad R, onda ti treba 8 matrica, 4 sa jedinicama, 4 sa i-ovima, tj. E1, E2, E3, E4, Ei11, Ei12, Ei21, Ei22. Jer je dim tog prostora 8.
_________________
Đante tanda fandiga?
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
mocibob
Forumaš(ica)

Pridružen/a: 08. 03. 2007. (10:26:53)
Postovi: (16)16
|
|
| [Vrh] |
|
maja m
Gost
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
maja m
Gost
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
maja m
Gost
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 0:45 sub, 8. 12. 2007 Naslov: Postano: 0:45 sub, 8. 12. 2007 Naslov: |
    |
|
|
Za nulu je. 8) Opceniti postupak je isti kao u onom mom dokazu: provjeravas uvjet da je nesto potprostor:
Neka su [latex]\textstyle x=(x_1,x_2,x_3,x_4), y=(y_1,y_2,y_3,y_4) \in \mathbb{R}^4[/latex] i [latex]\alpha, \beta \in \mathbb{R}[/latex]
Zanima nas vrijedi li:
[latex]\alpha x + \beta y \in S[/latex] :nosmile: (*)
gdje je [latex]S = \{(x_1,x_2,x_3,x_4) \in \mathbb{R}^4:\ x_1+x_2+x_3^3+x_4=0\}[/latex]
Uvrsti i provjeri; ako (*) vrijedi neovisno o [latex]\textstyle x, y, \alpha \textrm{ i } \beta[/latex], onda [latex]S[/latex] je podskup; inace nije. 8)
Za nulu je.  Opceniti postupak je isti kao u onom mom dokazu: provjeravas uvjet da je nesto potprostor: Opceniti postupak je isti kao u onom mom dokazu: provjeravas uvjet da je nesto potprostor:
Neka su 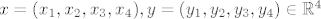 i i 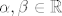
Zanima nas vrijedi li:
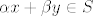  (*) (*)
gdje je 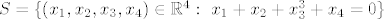
Uvrsti i provjeri; ako (*) vrijedi neovisno o 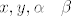 , onda , onda  je podskup; inace nije. je podskup; inace nije. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
 Postano: 0:54 sub, 8. 12. 2007 Naslov: Postano: 0:54 sub, 8. 12. 2007 Naslov: |
    |
|
|
E da je na desnoj strani nula onda bi opet bila ista stvar jer nemas izraz koji je linearan (onaj x3^3 stvara probleme). Npr. vektor (1,-1,1,-1) bi bio iz skupa S={(x1,x2,x3,x4)€R4 : x1+x2+x3^3+x4=0} ali vektor (2,-2,2,-2) nije jer ne zadovoljava uvjet. Stoga S nije vekt. prostor jer ako bi bio, onda bi svaka linearna kombinacija vektora iz S također morala biti iz S. Ali to nije slučaj jer smo našli v € S takav da 2v nije iz S.
Općenitio ako imas tako neki skup koji je podskup nekog vektorskog prostora, onda je dovoljno provjeriti da li je taj skup zatvoren na zbrajanje vektora i množenje skalarom, tj. da li za svaki v1,v2€S i t €F(skalar) vrijedi (t*v1+v2)€S. Ako da onda je S potprostor tog većeg prostra, a time je i sam vektorski prostor! :)
E da je na desnoj strani nula onda bi opet bila ista stvar jer nemas izraz koji je linearan (onaj x3^3 stvara probleme). Npr. vektor (1,-1,1,-1) bi bio iz skupa S={(x1,x2,x3,x4)€R4 : x1+x2+x3^3+x4=0} ali vektor (2,-2,2,-2) nije jer ne zadovoljava uvjet. Stoga S nije vekt. prostor jer ako bi bio, onda bi svaka linearna kombinacija vektora iz S također morala biti iz S. Ali to nije slučaj jer smo našli v € S takav da 2v nije iz S.
Općenitio ako imas tako neki skup koji je podskup nekog vektorskog prostora, onda je dovoljno provjeriti da li je taj skup zatvoren na zbrajanje vektora i množenje skalarom, tj. da li za svaki v1,v2€S i t €F(skalar) vrijedi (t*v1+v2)€S. Ako da onda je S potprostor tog većeg prostra, a time je i sam vektorski prostor! 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
maja m
Gost
|
|
| [Vrh] |
|
|















