| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 18:39 ned, 25. 11. 2007 Naslov: Re: razna pitanja Postano: 18:39 ned, 25. 11. 2007 Naslov: Re: razna pitanja |
    |
|
|
[quote="tihana"]http://web.math.hr/nastava/vekt/files/v1-kviz1-rj.pdf
na 3.stranici, zadatak treći
kako je tu dobiveno 2006 ? ja sam dobila 1506[/quote]
Rješenje koje piše u datoteci je točno. Naime, ako je [latex](A-2I)^{200}(A-3I)^{300}=0[/latex], onda znamo da minimalni polinom [latex]\mu_A[/latex] dijeli polinom [latex]p(\lambda):=(\lambda-2)^{200}(\lambda-3)^{300}[/latex]. Stoga imamo sljedeće mogućnosti za [latex]\mu_A[/latex]:
[latex]\mu_A(\lambda)=(\lambda-2)^{k}(\lambda-3)^{l}[/latex], gdje su [latex]k,l \in \mathbb{Z}_+,1\leq k+l \leq 2005[/latex] (primijetite da je dozvoljena i mogućnost [latex]k=0[/latex] odnosno [latex]l=0[/latex]). Kako pak [latex]\mu_A[/latex] dijeli i karakteristični polinom [latex]k_A[/latex] od [latex]A[/latex], [latex]k_A[/latex] može biti sljedećeg oblika:
[latex]k_A(\lambda)=-(\lambda-2)^{k}(\lambda-3)^{l}[/latex], pri čemu je [latex]k,l \in \mathbb{Z}_+, 1\leq k+l = 2005[/latex].
Takvih mogućnosti ima [latex]2006[/latex].
| tihana (napisa): | http://web.math.hr/nastava/vekt/files/v1-kviz1-rj.pdf
na 3.stranici, zadatak treći
kako je tu dobiveno 2006 ? ja sam dobila 1506 |
Rješenje koje piše u datoteci je točno. Naime, ako je 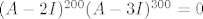 , onda znamo da minimalni polinom , onda znamo da minimalni polinom 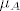 dijeli polinom dijeli polinom 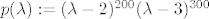 . Stoga imamo sljedeće mogućnosti za . Stoga imamo sljedeće mogućnosti za 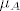 : :
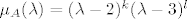 , gdje su , gdje su 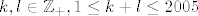 (primijetite da je dozvoljena i mogućnost (primijetite da je dozvoljena i mogućnost 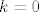 odnosno odnosno 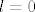 ). Kako pak ). Kako pak 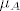 dijeli i karakteristični polinom dijeli i karakteristični polinom 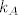 od od  , , 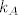 može biti sljedećeg oblika: može biti sljedećeg oblika:
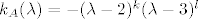 , pri čemu je , pri čemu je 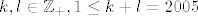 . .
Takvih mogućnosti ima 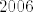 . .
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 23:04 ned, 25. 11. 2007 Naslov: Postano: 23:04 ned, 25. 11. 2007 Naslov: |
    |
|
|
[quote="sun"]2 pitanja
prvo mozete li malo objasniti kako se rjesava 7.zad u grupi C ili A
[/quote]
Dva operatora (nad kompleksnim prostorom) su slična ako i samo ako imaju jednake Jordanove forme (do na poredak blokova). Znači zadatk 7A/C se svodi na određivanje broja različitih mogućnosti za Jordanovu formu operatora [latex]A \in L(\mathbb{C}^3)[/latex] (do na poredak blokova) čiji je spektar jednak [latex]\sigma(A)=\{2,3\}[/latex]. Takvih je ukupno [latex]4[/latex]:
[latex]\left( \begin{array}{ccc}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 3 \\
\end{array} \right), \ \left( \begin{array}{ccc}
2 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 3 \\
\end{array} \right), \ \left( \begin{array}{ccc}
2 & 1 & 0 \\
0 & 2 & 0 \\
0 & 0 & 3 \\
\end{array} \right), \ \left( \begin{array}{ccc}
2 & 0 & 0 \\
0 & 3 & 1 \\
0 & 0 & 3 \\
\end{array} \right) [/latex].
[quote="sun"]
i drugo pitanje na str4. 6.zad (znaci grupa B) imamo zadano A^3+3A^2+2A=0, znaci da je minimalni polinom=lambda^3...=lamda(lamda+1)(lambda+2) zar iz toga ne slijedi da su svoj.vrijednosti 0,-1,-2?
kako onda u Ja imamo samo -1 i -2?
znam da zbog det = -4 ne moze biti 0, ali zar nije onda mozda krivo zadano?[/quote]
Ne, jedino što znate je da minimalni polinom [latex]\mu_A[/latex] dijeli polinom [latex]p(\lambda):=\lambda^3 + 3 \lambda^2 + 2 \lambda= \lambda(\lambda+1)(\lambda+2)[/latex]. To ne znači da svaki od faktora polinoma [latex]p[/latex] mora nastupiti u [latex]\mu_A[/latex].
Štoviše, iz uvjeta [latex]\det A =-4[/latex] znamo da je operator [latex]A[/latex] regularan, pa iz [latex]A^3+3A^2+2A=0[/latex] slijedi i [latex]A^2+3A+2I=(A+I)(A+2I)=0[/latex]. Odavde slijedi da je ili [latex]\mu_A(\lambda)=\lambda +1[/latex], ili [latex]\mu_A(\lambda)=\lambda +2[/latex], ili [latex]\mu_A(\lambda)=(\lambda +1)(\lambda +2)[/latex]. Prve dvije mogućnosti su nemoguće jer bi onda bilo [latex]A=-I[/latex] (u prvom slučaju), odnosno [latex]A=-2I[/latex] (u drugom slučaju), pa bi bilo [latex]\det A=(-1)^{7}=-1[/latex] (u prvom slučaju), odnosno [latex]\det A=(-2)^{7}=-128[/latex] (u drugom slučaju).
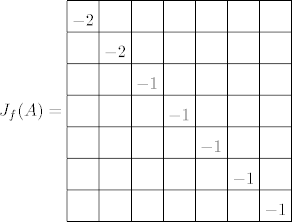
Zaključujemo da je [latex]\mu_A(\lambda)=(\lambda +1)(\lambda +2)[/latex]. Dakle, [latex]A[/latex] je dijagonalizabilan i [latex]\sigma(A)=\{-2,-1\}[/latex]. Napokon, iz [latex]\det A =-4[/latex] slijedi da je
[latex]J_f(A)=
\begin{tabular}{|c|c|c|c|c|c|c|}
\hline
$\!\!\!\!-2\!\!\!\!$\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm}\\
\hline
\rule{3mm}{0mm}\rule{0mm}{5mm} & $\!\!\!\!-2\!\!\!\!$\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm}\\
\hline
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm} &
$\!\!\!\!-1\!\!\!\!$\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm}\\
\hline
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} & $\!\!\!\!-1\!\!\!\!$\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm}\\
\hline
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm} &
$\!\!\!\!-1\!\!\!\!$\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm}\\
\hline
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} &
$\!\!\!\!-1\!\!\!\!$\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm}\\
\hline
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} & \rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} &
\rule{3mm}{0mm}\rule{0mm}{5mm} & $\!\!\!\!-1\!\!\!\!$\rule{0mm}{5mm}\\
\hline
\end{tabular}\\
\rule{0mm}{0mm}\\\end{tabular}
[/latex]
| sun (napisa): | 2 pitanja
prvo mozete li malo objasniti kako se rjesava 7.zad u grupi C ili A
|
Dva operatora (nad kompleksnim prostorom) su slična ako i samo ako imaju jednake Jordanove forme (do na poredak blokova). Znači zadatk 7A/C se svodi na određivanje broja različitih mogućnosti za Jordanovu formu operatora 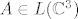 (do na poredak blokova) čiji je spektar jednak (do na poredak blokova) čiji je spektar jednak 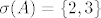 . Takvih je ukupno . Takvih je ukupno 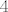 : :
 . .
| sun (napisa): |
i drugo pitanje na str4. 6.zad (znaci grupa B) imamo zadano A^3+3A^2+2A=0, znaci da je minimalni polinom=lambda^3...=lamda(lamda+1)(lambda+2) zar iz toga ne slijedi da su svoj.vrijednosti 0,-1,-2?
kako onda u Ja imamo samo -1 i -2?
znam da zbog det = -4 ne moze biti 0, ali zar nije onda mozda krivo zadano? |
Ne, jedino što znate je da minimalni polinom 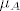 dijeli polinom dijeli polinom 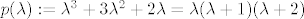 . To ne znači da svaki od faktora polinoma . To ne znači da svaki od faktora polinoma  mora nastupiti u mora nastupiti u 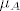 . .
Štoviše, iz uvjeta 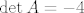 znamo da je operator znamo da je operator  regularan, pa iz regularan, pa iz 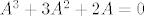 slijedi i slijedi i 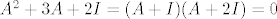 . Odavde slijedi da je ili . Odavde slijedi da je ili 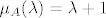 , ili , ili 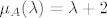 , ili , ili 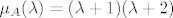 . Prve dvije mogućnosti su nemoguće jer bi onda bilo . Prve dvije mogućnosti su nemoguće jer bi onda bilo  (u prvom slučaju), odnosno (u prvom slučaju), odnosno 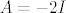 (u drugom slučaju), pa bi bilo (u drugom slučaju), pa bi bilo 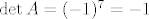 (u prvom slučaju), odnosno (u prvom slučaju), odnosno 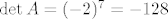 (u drugom slučaju). (u drugom slučaju).
Zaključujemo da je 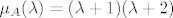 . Dakle, . Dakle,  je dijagonalizabilan i je dijagonalizabilan i 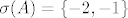 . Napokon, iz . Napokon, iz 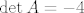 slijedi da je slijedi da je
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
zoja
Forumaš(ica)

Pridružen/a: 16. 01. 2007. (00:39:43)
Postovi: (23)16
Spol: 
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 15:33 sri, 28. 11. 2007 Naslov: Postano: 15:33 sri, 28. 11. 2007 Naslov: |
    |
|
|
Nešt me malo zbunjuje, rekli smo da je u zapisu minimalnog polinoma [latex]\mu _A = \prod\limits_{i = 1}^s {\left( {\lambda - \lambda _i } \right)^{p_i } }[/latex], [latex]p_i[/latex] prestavlja broj blokova u Jordanovoj formi kojima pripada svojstvena vrijednost [latex]{\lambda _i }[/latex]. To je ekvivalentno tome da je [latex]p_i[/latex] geometrijska kratnost od [latex]{\lambda _i }[/latex].
E sad, znam da je svaka svojstvena vrijednost nultočka karakterističnog polinoma i pojavljuje mi se u njegovom rastavu na linearne faktore, a znam da joj je geometrijska kratnost barem 1 (pripada joj barem jedan blok) pa bi se morala pojavit i u rastavu minimalnog polinoma. Dakle [latex]\sigma \left( A \right) = \left\{ {\lambda \in K:k_A \left( \lambda \right) = 0} \right\} = \left\{ {\lambda \in K:\mu _A \left( \lambda \right) = 0} \right\}[/latex]. Ali to izgleda nije istina. Gdje mi je greška u zaključivanju?
Edit: ok, skužio sam, potencija u minimalnom je dimenzija najvećeg bloka, a ne ovo što sam napiso
Nešt me malo zbunjuje, rekli smo da je u zapisu minimalnog polinoma 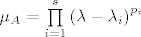 , , 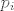 prestavlja broj blokova u Jordanovoj formi kojima pripada svojstvena vrijednost prestavlja broj blokova u Jordanovoj formi kojima pripada svojstvena vrijednost 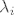 . To je ekvivalentno tome da je . To je ekvivalentno tome da je 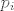 geometrijska kratnost od geometrijska kratnost od 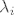 . .
E sad, znam da je svaka svojstvena vrijednost nultočka karakterističnog polinoma i pojavljuje mi se u njegovom rastavu na linearne faktore, a znam da joj je geometrijska kratnost barem 1 (pripada joj barem jedan blok) pa bi se morala pojavit i u rastavu minimalnog polinoma. Dakle 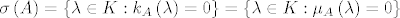 . Ali to izgleda nije istina. Gdje mi je greška u zaključivanju? . Ali to izgleda nije istina. Gdje mi je greška u zaključivanju?
Edit: ok, skužio sam, potencija u minimalnom je dimenzija najvećeg bloka, a ne ovo što sam napiso
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 15:48 sri, 28. 11. 2007 Naslov: Postano: 15:48 sri, 28. 11. 2007 Naslov: |
    |
|
|
[quote="alen"]Nešt me malo zbunjuje, rekli smo da je u zapisu minimalnog polinoma [latex]\mu _A = \prod\limits_{i = 1}^s {\left( {\lambda - \lambda _i } \right)^{p_i } }[/latex], [latex]p_i[/latex] prestavlja broj blokova u Jordanovoj formi kojima pripada svojstvena vrijednost [latex]{\lambda _i }[/latex]. To je ekvivalentno tome da je [latex]p_i[/latex] geometrijska kratnost od [latex]{\lambda _i }[/latex].
E sad, znam da je svaka svojstvena vrijednost nultočka karakterističnog polinoma i pojavljuje mi se u njegovom rastavu na linearne faktore, a znam da joj je geometrijska kratnost barem 1 (pripada joj barem jedan blok) pa bi se morala pojavit i u rastavu minimalnog polinoma. Dakle [latex]\sigma \left( A \right) = \left\{ {\lambda \in K:k_A \left( \lambda \right) = 0} \right\} = \left\{ {\lambda \in K:\mu _A \left( \lambda \right) = 0} \right\}[/latex]. Ali to izgleda nije istina. Gdje mi je greška u zaključivanju?
[/quote]
Od kud si zaključio da [latex]p_i[/latex] predstavlja broj blokova u Jordanovoj formi obzirom na svojstvenu vrijednost [latex]{\lambda _i }[/latex]? To (općenito) nije točno, [latex]p_i[/latex] predstavlja dimenziju maksimalne Jordanove klijetke pridružene svojoj svojstvenoj vrijednost [latex]{\lambda _i }[/latex].
I ovo što si napisao
[quote="alen"]
[latex]\sigma \left( A \right) = \left\{ {\lambda \in K:k_A \left( \lambda \right) = 0} \right\} = \left\{ {\lambda \in K:\mu _A \left( \lambda \right) = 0} \right\}[/latex].
[/quote]
je uistinu točno. :D
| alen (napisa): | Nešt me malo zbunjuje, rekli smo da je u zapisu minimalnog polinoma 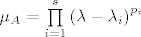 , , 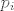 prestavlja broj blokova u Jordanovoj formi kojima pripada svojstvena vrijednost prestavlja broj blokova u Jordanovoj formi kojima pripada svojstvena vrijednost 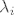 . To je ekvivalentno tome da je . To je ekvivalentno tome da je 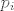 geometrijska kratnost od geometrijska kratnost od 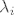 . .
E sad, znam da je svaka svojstvena vrijednost nultočka karakterističnog polinoma i pojavljuje mi se u njegovom rastavu na linearne faktore, a znam da joj je geometrijska kratnost barem 1 (pripada joj barem jedan blok) pa bi se morala pojavit i u rastavu minimalnog polinoma. Dakle 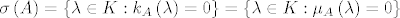 . Ali to izgleda nije istina. Gdje mi je greška u zaključivanju? . Ali to izgleda nije istina. Gdje mi je greška u zaključivanju?
|
Od kud si zaključio da 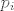 predstavlja broj blokova u Jordanovoj formi obzirom na svojstvenu vrijednost predstavlja broj blokova u Jordanovoj formi obzirom na svojstvenu vrijednost 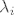 ? To (općenito) nije točno, ? To (općenito) nije točno, 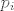 predstavlja dimenziju maksimalne Jordanove klijetke pridružene svojoj svojstvenoj vrijednost predstavlja dimenziju maksimalne Jordanove klijetke pridružene svojoj svojstvenoj vrijednost 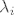 . .
I ovo što si napisao
| alen (napisa): |
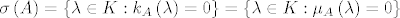 . .
|
je uistinu točno. 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
|









