|
Što točno znači odrediti parametre u sustavu jednadžbi da on ima [b]jedinstveno[/b] rješenje?
Konkretno, bio je zadatak sad na kolokviju:
[quote="zadatak"]Odredite [latex]\beta, \gamma \in \mathbb{R}[/latex] tako da sustav
[latex]x+5y-3z=1[/latex]
[latex]-3x-16y+ \beta z=2 \gamma[/latex]
[latex]2x+12y+8z=1[/latex]
ima
(a) jedinstveno rješenje
(b) beskonačno mnogo rješenja
(c) nema rješenja.
U slučajevima kad sustav ima rješenja, odredite skup rješenja.[/quote]
Sustav možemo zapisati matrično:
[latex]\left(\begin{array}{ccc|c}1&5&-3&1
\\-3&-16&\beta&2 \gamma
\\2&12&8&1 \end{array} \right)[/latex]
i Gaussovim transformacijama doći do gornjetrokutaste forme (vrlo je moguće da je ovo fulano, ali dobro, bitan je princip :wink: :
[latex]\left(\begin{array}{ccc|c}1&5&-3&1
\\0&1&9 - \beta&-2 \gamma-3
\\0&0&1&\frac{4 \gamma+5}{2 \beta -4} \end{array} \right)[/latex]
Iz čega slijedi da je [latex]z=\frac{4 \gamma+5}{2 \beta -4}[/latex].
Ovdje odmah možemo odgovoriti na pitanje [b](c)[/b], jer ako je [latex]\beta=2[/latex], sustav [b]nema rješenja[/b]. Nula u nazivniku, i tako, to je jasno.
Idemo promatrati kakvog će oblika biti rješenja ovog sustava za parametre [latex]\beta \in \mathbb{R} $ \textbackslash \textbraceleft 2\textbraceright$ , \gamma \in \mathbb{R}[/latex]. Uvrštavanjem izraza za z [latex](z=\frac{4 \gamma+5}{2 \beta -4})[/latex] u gornji sustav slijedi:
[latex]y=\frac{-(\beta +28 \gamma + 33)}{2 \beta -4}[/latex]
[latex]x=\frac{7 \beta +152 \gamma + 176}{2 \beta -4}[/latex]
Kako [latex]\beta[/latex] i [latex]\gamma[/latex] šeću po [latex]\mathbb{R}[/latex] (i naravno [latex]\beta \neq 2[/latex]) tako u ovisnosti o njima dobivamo različite trojke realnih brojeva (x,y,z) koje zadovoljavaju početni sustav, dakle imamo dvoparametarsku familiju rješenja, kojih naravno ima [b]beskonačno[/b] mnogo, pa je rješenje pitanja [b](b)[/b] sljedeći skup uređenih trojki realnih brojeva:
[latex](x,y,z)=$\textbraceleft$ (\frac{7 \beta +152 \gamma + 176}{2 \beta -4} ,
\frac{-(\beta +28 \gamma + 33)}{2 \beta -4} ,
\frac{4 \gamma+5}{2 \beta -4}); \beta \in \mathbb{R} $ \textbackslash \textbraceleft 2\textbraceright$ , \gamma \in \mathbb{R} $\textbraceright$[/latex]
Jel' tako? :)
No ono što me stvarno zanima je kako odgovoriti na pitanje (a) - kakvi moraju biti [latex]\beta[/latex] i [latex]\gamma[/latex] da bi početni, zadani sustav imao [i]jedinstveno[/i] rješenje. I što je uopće u ovom kontekstu jedinstveno rješenje? Zbunjuje me to što smo za rješenja npr. kvadratne jednadžbe rekli da ima jedinstveno rješenje ako je [latex]x_1=x_2[/latex]. Je li rješenje ovog sustava od 3 jednadžbe s 3 nepoznanice iz kolokvija jedinstveno ako je x=y=z, pa se izrazi za x, y i z izjednače? Što, kako, zašto?
:shock:
Što točno znači odrediti parametre u sustavu jednadžbi da on ima jedinstveno rješenje?
Konkretno, bio je zadatak sad na kolokviju:
| zadatak (napisa): | Odredite  tako da sustav tako da sustav

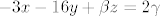
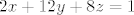
ima
(a) jedinstveno rješenje
(b) beskonačno mnogo rješenja
(c) nema rješenja.
U slučajevima kad sustav ima rješenja, odredite skup rješenja. |
Sustav možemo zapisati matrično:
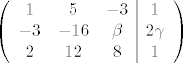
i Gaussovim transformacijama doći do gornjetrokutaste forme (vrlo je moguće da je ovo fulano, ali dobro, bitan je princip  : :
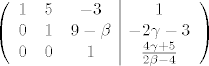
Iz čega slijedi da je 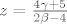 . .
Ovdje odmah možemo odgovoriti na pitanje (c), jer ako je 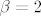 , sustav nema rješenja. Nula u nazivniku, i tako, to je jasno. , sustav nema rješenja. Nula u nazivniku, i tako, to je jasno.
Idemo promatrati kakvog će oblika biti rješenja ovog sustava za parametre  . Uvrštavanjem izraza za z . Uvrštavanjem izraza za z 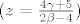 u gornji sustav slijedi: u gornji sustav slijedi:
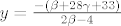
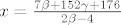
Kako 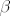 i i 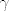 šeću po šeću po  (i naravno (i naravno 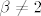 ) tako u ovisnosti o njima dobivamo različite trojke realnih brojeva (x,y,z) koje zadovoljavaju početni sustav, dakle imamo dvoparametarsku familiju rješenja, kojih naravno ima beskonačno mnogo, pa je rješenje pitanja (b) sljedeći skup uređenih trojki realnih brojeva: ) tako u ovisnosti o njima dobivamo različite trojke realnih brojeva (x,y,z) koje zadovoljavaju početni sustav, dakle imamo dvoparametarsku familiju rješenja, kojih naravno ima beskonačno mnogo, pa je rješenje pitanja (b) sljedeći skup uređenih trojki realnih brojeva:
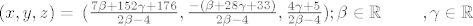
Jel' tako? 
No ono što me stvarno zanima je kako odgovoriti na pitanje (a) - kakvi moraju biti 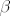 i i 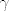 da bi početni, zadani sustav imao jedinstveno rješenje. I što je uopće u ovom kontekstu jedinstveno rješenje? Zbunjuje me to što smo za rješenja npr. kvadratne jednadžbe rekli da ima jedinstveno rješenje ako je da bi početni, zadani sustav imao jedinstveno rješenje. I što je uopće u ovom kontekstu jedinstveno rješenje? Zbunjuje me to što smo za rješenja npr. kvadratne jednadžbe rekli da ima jedinstveno rješenje ako je 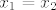 . Je li rješenje ovog sustava od 3 jednadžbe s 3 nepoznanice iz kolokvija jedinstveno ako je x=y=z, pa se izrazi za x, y i z izjednače? Što, kako, zašto? . Je li rješenje ovog sustava od 3 jednadžbe s 3 nepoznanice iz kolokvija jedinstveno ako je x=y=z, pa se izrazi za x, y i z izjednače? Što, kako, zašto?

Zadnja promjena: blob; 7:12 sri, 5. 12. 2007; ukupno mijenjano 1 put.
|






