2 komada sa zadnjeg roka (zadatak)

[ta2a]

1. Štap duljine L je slučajno razlomljen na tri dijela. Izračunajte vjerojatnost da je duljina najduljeg dijela manja od L/2.

2. Mali Ivica baca simetričnu kocku. Potom baci onoliko simetričnih kocaka koliki je rezultat prvog bacanja. Izračunajte vjerojatnost da se u oba bacanja zajedno pojavi točno jedna petica.

ne treba mi cijelo rješenje, sam kak počet

_________________
Nema kina do Fakina!

[ma]

mislim da drugi možemo ovako:

definiramo događaj - i potpuni sistem događaja - .

znamo:
;
;

sada je , ako me račun nije prevario

_________________
ima let u finish

[Ana]

Sve je ok, osim toga da je

P(A|H_5) = 5^5/6^5.

I mislim da onda ispada 0.3302.

[Ana]

A prvi...


A = {duljina najduljeg dijela <= L/2} = {duljina svakog dijela <= L/2} = {(x,y): x<=L/2, y-x<=L/2, L-y<=L/2} = {(x,y): x<=L/2, y<=x+L/2, y>=L/2}

omega = {(x,y): x<=y}

lambda(omega) = (L^2)/2
lambda(A) = ((L^2)/4)/2 = (L^2)/8

=> P(A) = 1/4.

[ma]

[Ana]

Zato što, ako si dobio peticu u prvom bacanju, u drugom smiješ dobiti sve osim petice.

A ti u slučaju H_5 dopuštaš da ti i u drugom bacanju dođe petica, ali mi
trebamo samo jednu u oba bacanja...

[ma]

[Ana]

Pogledaj si formulu za P(A|H_i).

E sad, recimo da je u prvom bacanju pala trojka (i=3). Znači, treba nam točno jedna petica u drugom bacanju.

Po formuli biramo jedno od tri mjesta na koje će pasti petica i onda još na dva mjesta možemo dobiti sve brojeve, osim petice => 3*5^2.
Jasno, dijelimo s 6^3.
Tu nije ništa sporno.


Uzmimo sad slučaj da je u prvom bacanju pala petica (i=5).

Ti sad tvrdiš da je ista formula P(A|H_i) primjenjiva i u tom slučaju.
Kad bi bilo tako, onda bismo birali jedno od 5 mjesta za peticu i na ostala četiri mjesta bismo mogli dobiti sve osim petice => 5*5^4.

Ali! Kako si već dobio peticu, u drugom bacanju je ne smiješ dobiti pa je broj svih kombinacija = 5^5.


Ok, sad sam skužila da smo dobili isto, ali to je samo zato što imamo šest brojeva. To je pogrešan način razmišljanja!

Jer, šta bi bilo kad bismo umjesto 5 imali zadano da trebamo dobiti točno jednu četvorku i da nam je u prvom bacanju pala četvorka?

Onda bismo, po tebi, imali: 4*5^3, što je različito od 5^4 - a to je broj kombinacija u kojima u drugom bacanju zabranjujemo pojavljivanje četvorke

[ma]

ali upravo je u tome stvar: ja sam definirao potpuni sistem događaja za ovaj određeni zadatak. ona formula ne pokazuje moj način razmišljanja.

pri rješavanju, posebno sam izdvojio slučaj kada prvo padne petica i uvidio da je 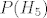(slučajno) moguće izračunati tom generalnom formulom za ostale slučajeve.
složit ću se s tobom, da bi mi to moglo npr oduzeti bodove na ispitu (makar je meni to bezveze), ali pošto je rezultat isti, nije mi se dalo izdvajati taj jedan slučaj. dakle, način razmišljanja mi je bio dobar, ali mi je vjerojatno način zapisivanja bio nedobar (šteta jer se baš fino posložilo).
svejedno, rezultati nam se ne poklapaju- bit će da sam fulao negdje u brzom računu.

_________________
ima let u finish

[Ana]

Da, i mene je drugačiji rezultat (možda moj ne valja ) naveo na to da si previdio slučaj za H_5, ali kad sam maloprije računala, skužila sam da formula u ovom slučaju vrijedi i da zbog petice dobivamo isto.

Znam da formula ne pokazuje tvoj način razmišljanja, ali ta2a je tražila logiku, a ne konačni rezultat, pa nek' smo mi to raščistili

[ma]

[Ana]

Ma glavno da nismo zbunili ta2u