Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

5. zadaća
WWW:

Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 2. godine -> Diskretna matematika
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 15:05 čet, 13. 12. 2007    Naslov: 5. zadaća Citirajte i odgovorite
Topic će bit otvoren prije ili kasnije, pa bolje prije...

Par pitanja:
U 2.zad razvijemo tu fju u red pa pročitamo a_n? Ako može mali hint... :beg:
Koji je to niz u 8.a? :grebgreb:
A evo i mojih rješenja (vj sam negdje zeznuo u računu pa ih uzimajte s rezervom... :lol:) :

[latex] 1.a) \frac{-x^{3}}{(1+x)^{2}}[/latex]
[latex]b) \frac {1}{(1+ax)^{n}}[/latex]
[latex]c) \frac {2x \cdot (5-2x)}{(1-x)^{3}} [/latex]

d) puno posla, a isto ko i ovi prije, ona suma je suma prvih n kvadrata, za to imamo formulu pa se to sređuje (zasad mi se ne da zezat s tim)

4. 12117
5. 9
[latex]8.b) \frac{e^{2x}}{x}+1

c) e^{x} \cdot (x^{2}+3x+1)

\sum_{n>=0} {\frac { (n+1)^{2}}{n!}} = e^{1} (1+3*1+1)=5e
[/latex]

9. 19480

Za one koji se žele priključit rješavanju,a nemju zadaću pri ruci, zadaci su [url=http://web.math.hr/nastava/komb/zadace/zadaca5.pdf]tu[/url]
Topic će bit otvoren prije ili kasnije, pa bolje prije...

Par pitanja:
U 2.zad razvijemo tu fju u red pa pročitamo a_n? Ako može mali hint... Molim, kumim i preklinjem!
Koji je to niz u 8.a? Kotacici rade 100 na sat
A evo i mojih rješenja (vj sam negdje zeznuo u računu pa ih uzimajte s rezervom... Laughing) :





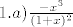
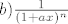
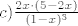
d) puno posla, a isto ko i ovi prije, ona suma je suma prvih n kvadrata, za to imamo formulu pa se to sređuje (zasad mi se ne da zezat s tim)

4. 12117
5. 9


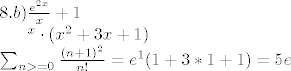
9. 19480

Za one koji se žele priključit rješavanju,a nemju zadaću pri ruci, zadaci su tu



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
stuey
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol: muško
Sarma = la pohva - posuda
39 = 41 - 2
Lokacija: Rijeka, Zg
PostPostano: 23:27 čet, 13. 12. 2007    Naslov: Citirajte i odgovorite
da, u 2.zad tocno to radis, razvijes u red i iscitas a_n.

u 8.a mislim da nemas sto drugo nego razviti u red i ispisat prva 4 clana (meni doslo [latex]1+7x+11/2x^2+1/2x^3[/latex])

1.a) dosao mi slicno kao tebi, ali [latex](1-x)^2[/latex] u nazivniku. moguce da sam falio, samo ne znam gdje mi je greska :?

pod b) dobijem [latex](1-ax)^{-n}[/latex]

c) nam je isti.

d) [latex]\frac{x^2+x}{(1-x)^4}[/latex]

u 4. imam 100 grešaka, pa nisam siguran za rješenje, ali došlo mi je 9099.

8.b) imam slično ali malo drukčije : [latex]1+x\cdot e^{2x}[/latex]

8.c) isto ko i tebi.
9.također.

edit: u 1.b) je 1-[b]a[/b]x, zaboravih na a
da, u 2.zad tocno to radis, razvijes u red i iscitas a_n.

u 8.a mislim da nemas sto drugo nego razviti u red i ispisat prva 4 clana (meni doslo )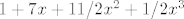

1.a) dosao mi slicno kao tebi, ali 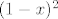u nazivniku. moguce da sam falio, samo ne znam gdje mi je greska Confused

pod b) dobijem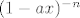

c) nam je isti.

d)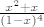

u 4. imam 100 grešaka, pa nisam siguran za rješenje, ali došlo mi je 9099.

8.b) imam slično ali malo drukčije :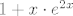

8.c) isto ko i tebi.
9.također.

edit: u 1.b) je 1-ax, zaboravih na a


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 23:54 čet, 13. 12. 2007    Naslov: Citirajte i odgovorite
Reko bi da u 1.a i b mora bit taj + u nazivniku jer kad razviješ u red ima onaj (-1)^n pa kod tog geom reda mora bit + u nazivniku...

a jel može koji hint za taj 2.b? Nešto sam zašteko... :oops:
[latex]a) a_n = 16{4 \choose n}(-2)^n[/latex]
[latex]c) a_n=- \frac{3^n}{n}[/latex], s tim da nisam ziher za ovaj pod c jer mi red ide od 1 pa bi to možda bio a{n+1}...
a pod d se ide parc razlomcima pa onda na geom red...

edit: još jedno pitanje u vezi 4. zadatka. Ja sam taj zadatak gledo s obzirom na pakete pa imamo jedn x1+x2+x3+x4=120 gdje je 6<=xi<=40. Sad sam to sad još pojednostavio (jer su paketi isti) y1+y2+y3+y4=96 0<=yi<=34. Tek sad sad pisao fju izvodnicu i gledao koef, u ovom slučaju uz x^96. Jel to može tak ili se mora odmah pisat fja izv pa izlučivat x^6 iz svake zagrade pa onda gledat koef uz x^120? :grebgreb:

edit2: Imate pravo za 1.b. Ide minus. Ja kriv. :)
Reko bi da u 1.a i b mora bit taj + u nazivniku jer kad razviješ u red ima onaj (-1)^n pa kod tog geom reda mora bit + u nazivniku...

a jel može koji hint za taj 2.b? Nešto sam zašteko... Embarassed

, s tim da nisam ziher za ovaj pod c jer mi red ide od 1 pa bi to možda bio a{n+1}...
a pod d se ide parc razlomcima pa onda na geom red...

edit: još jedno pitanje u vezi 4. zadatka. Ja sam taj zadatak gledo s obzirom na pakete pa imamo jedn x1+x2+x3+x4=120 gdje je 6⇐xi⇐40. Sad sam to sad još pojednostavio (jer su paketi isti) y1+y2+y3+y4=96 0⇐yi⇐34. Tek sad sad pisao fju izvodnicu i gledao koef, u ovom slučaju uz x^96. Jel to može tak ili se mora odmah pisat fja izv pa izlučivat x^6 iz svake zagrade pa onda gledat koef uz x^120? Kotacici rade 100 na sat

edit2: Imate pravo za 1.b. Ide minus. Ja kriv. Smile



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy

Zadnja promjena: Luuka; 0:53 pet, 14. 12. 2007; ukupno mijenjano 5 put/a.
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
matmih
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: muško
Sarma = la pohva - posuda
36 = 51 - 15
Lokacija: {Zg, De , Ri}
PostPostano: 0:27 pet, 14. 12. 2007    Naslov: Citirajte i odgovorite
U 1.a) treba doći 1+x u nazivniku, ali u 1.b) ide minus kako je stuey napisao, taj ide pomoću binomne formule, ja bi rekao...
i 1.c) je točan, dalje nisam još došao za sada.
U 1.a) treba doći 1+x u nazivniku, ali u 1.b) ide minus kako je stuey napisao, taj ide pomoću binomne formule, ja bi rekao...
i 1.c) je točan, dalje nisam još došao za sada.


[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
stuey
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol: muško
Sarma = la pohva - posuda
39 = 41 - 2
Lokacija: Rijeka, Zg
PostPostano: 0:55 pet, 14. 12. 2007    Naslov: Citirajte i odgovorite
[quote="Luuka"]
a jel može koji hint za taj 2.zad? Nešto sam zašteko... :oops:
[/quote]

2.a) raspišeš pomoću binomne formule, ja sam rješenje dobio u 2-3 koraka već, ak nisam nešto gadno falio :)

u 2.b) prvo razviješ [latex]e^{7x}[/latex] u red, pa onda dalje, nadam se da je dovoljan hint ;)
ps. u tom 2.b) se dobije niz u kojem je vrijednost općeg člana dobra za sve članove niza, osim za [latex]a_3[/latex], za njega je mrvicu drukčiji izraz.

2.d) rastaviš pomoću parcijalnih razlomaka, i onda svaki od dva dobivena pribrojnika naštimaš tako da ih možeš razviti u geometrijski red.

za 4. nisam siguran smije li se tako, malo je kasno već :)
Luuka (napisa):

a jel može koji hint za taj 2.zad? Nešto sam zašteko... Embarassed


2.a) raspišeš pomoću binomne formule, ja sam rješenje dobio u 2-3 koraka već, ak nisam nešto gadno falio Smile

u 2.b) prvo razviješ 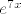u red, pa onda dalje, nadam se da je dovoljan hint Wink
ps. u tom 2.b) se dobije niz u kojem je vrijednost općeg člana dobra za sve članove niza, osim za 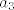, za njega je mrvicu drukčiji izraz.

2.d) rastaviš pomoću parcijalnih razlomaka, i onda svaki od dva dobivena pribrojnika naštimaš tako da ih možeš razviti u geometrijski red.

za 4. nisam siguran smije li se tako, malo je kasno već Smile


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 9:21 pet, 14. 12. 2007    Naslov: Citirajte i odgovorite
Hvala stuey, al čak sam se i sam sjetio kak bi to išlo (editirah post 2 min prije tvog posta)... ali svejedno :karma: za trud u 1 ujutro... :lol:
Hvala stuey, al čak sam se i sam sjetio kak bi to išlo (editirah post 2 min prije tvog posta)... ali svejedno karma++ za trud u 1 ujutro... Laughing



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
mala
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 10. 10. 2006. (16:13:20)
Postovi: (2A)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
6 = 7 - 1
PostPostano: 10:09 pet, 14. 12. 2007    Naslov: Citirajte i odgovorite
1.c) (-10x+4x)/(x-1)^3 :wink:
ah da, u brojniku je plus, tek sad vidim :oops:
1.c) (-10x+4x)/(x-1)^3 Wink
ah da, u brojniku je plus, tek sad vidim Embarassed


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 12:27 ned, 16. 12. 2007    Naslov: Citirajte i odgovorite
[quote="Luuka"]još jedno pitanje u vezi 4. zadatka. Ja sam taj zadatak gledo s obzirom na pakete pa imamo jedn x1+x2+x3+x4=120 gdje je 6<=xi<=40. Sad sam to sad još pojednostavio (jer su paketi isti) y1+y2+y3+y4=96 0<=yi<=34. Tek sad sad pisao fju izvodnicu i gledao koef, u ovom slučaju uz x^96. Jel to može tak ili se mora odmah pisat fja izv pa izlučivat x^6 iz svake zagrade pa onda gledat koef uz x^120? :grebgreb: [/quote]

Da sam sebi odgovorim: Može se pojednostavit, dođe isto. ;)

edit: Pitanje - da li svaki an mora krenut od 0 ili mogu reć da je an=nešto, za n iz N? Ili kad pomaknem indexe u redu još posebno izdvojim a0?
Luuka (napisa):
još jedno pitanje u vezi 4. zadatka. Ja sam taj zadatak gledo s obzirom na pakete pa imamo jedn x1+x2+x3+x4=120 gdje je 6⇐xi⇐40. Sad sam to sad još pojednostavio (jer su paketi isti) y1+y2+y3+y4=96 0⇐yi⇐34. Tek sad sad pisao fju izvodnicu i gledao koef, u ovom slučaju uz x^96. Jel to može tak ili se mora odmah pisat fja izv pa izlučivat x^6 iz svake zagrade pa onda gledat koef uz x^120? Kotacici rade 100 na sat


Da sam sebi odgovorim: Može se pojednostavit, dođe isto. Wink

edit: Pitanje - da li svaki an mora krenut od 0 ili mogu reć da je an=nešto, za n iz N? Ili kad pomaknem indexe u redu još posebno izdvojim a0?



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 19:30 ned, 16. 12. 2007    Naslov: Citirajte i odgovorite
Rekurzija, 3.zad. Molio bih pomoć jer stalno nešt zeznem...

Hint za one redove sa a{n+1} i a{n+2}

Ovo je editiran post, pa ak je netko vidio kaj sam ranije napiso, nek to izbriše iz svog sjećanja...

edit: našo sam si grešku, rekurzija riješena... :lol:

edit2:
[quote="stuey"]8.b) imam slično ali malo drukčije : [latex]1+x\cdot e^{2x}[/latex][/quote]
Tebi je točno, našo sam si grešku ;)
Rekurzija, 3.zad. Molio bih pomoć jer stalno nešt zeznem...

Hint za one redove sa a{n+1} i a{n+2}

Ovo je editiran post, pa ak je netko vidio kaj sam ranije napiso, nek to izbriše iz svog sjećanja...

edit: našo sam si grešku, rekurzija riješena... Laughing

edit2:
stuey (napisa):
8.b) imam slično ali malo drukčije :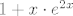

Tebi je točno, našo sam si grešku Wink



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy

Zadnja promjena: Luuka; 20:16 ned, 16. 12. 2007; ukupno mijenjano 1 put.
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
sun
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: žensko
Sarma = la pohva - posuda
22 = 23 - 1
PostPostano: 19:50 ned, 16. 12. 2007    Naslov: Citirajte i odgovorite
a ja sam to radila slino kao na vjezbama
samo sto nemas f(x)*x, f(x)*x^2 nego f(x)/x
pa bi po meni red za an+2
bio fx/x^2 - a0/x^2 - a1/x^2 itd
ali nisam sigurna
a ja sam to radila slino kao na vjezbama
samo sto nemas f(x)*x, f(x)*x^2 nego f(x)/x
pa bi po meni red za an+2
bio fx/x^2 - a0/x^2 - a1/x^2 itd
ali nisam sigurna


[Vrh]
Korisnički profil Pošaljite privatnu poruku
napraviculom
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: muško
Sarma = la pohva - posuda
14 = 16 - 2
Lokacija: Scranton
PostPostano: 23:43 ned, 16. 12. 2007    Naslov: Citirajte i odgovorite
ajde ako je netko rijesio taj 3. nek stavi rjesenje ili bar f(x), molim lijepo.
ajde ako je netko rijesio taj 3. nek stavi rjesenje ili bar f(x), molim lijepo.



_________________
"I'm the operator with my pocket calculator"
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 23:52 ned, 16. 12. 2007    Naslov: Citirajte i odgovorite
Eto u attachmentu ;)
Eto u attachmentu Wink



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
napraviculom
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: muško
Sarma = la pohva - posuda
14 = 16 - 2
Lokacija: Scranton
PostPostano: 14:44 pon, 17. 12. 2007    Naslov: Citirajte i odgovorite
hvala Luuka. k++ u svakom slucaju.
edit: ali cini mi se da desnu stranu treba jos pomnozit s x^2 (obje sume) gore na pocetkujer ti red s desne strane isto ide od 2. mozda sam u krivu.

2 (b) bi onda bilo 7^{n-1} / (n-1)! , n>=1 , n razlicito od 3,
a_3=15/2.
ima li to smisla?
hvala Luuka. k++ u svakom slucaju.
edit: ali cini mi se da desnu stranu treba jos pomnozit s x^2 (obje sume) gore na pocetkujer ti red s desne strane isto ide od 2. mozda sam u krivu.

2 (b) bi onda bilo 7^{n-1} / (n-1)! , n>=1 , n razlicito od 3,
a_3=15/2.
ima li to smisla?



_________________
"I'm the operator with my pocket calculator"
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 21:11 pon, 17. 12. 2007    Naslov: Citirajte i odgovorite
Rekurzija je ziher dobra..

A 2.b je:
[latex]a_n = \frac{7^{n-1}}{(n-1)!} , n \in N \setminus \{ 3 \}[/latex]

[latex]a_0=0, a_3 = \frac{7^2}{2!} + 1= \frac{51}{2}[/latex]
Rekurzija je ziher dobra..

A 2.b je:





_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
ma
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: muško
Sarma = la pohva - posuda
58 = 89 - 31
PostPostano: 23:42 pon, 17. 12. 2007    Naslov: Citirajte i odgovorite
[quote="Luuka"]A 2.b je:
[latex]a_n = \frac{7^{n-1}}{(n-1)!} , n \in N \setminus \{ 3 \}[/latex]

[latex]a_0=0, a_3 = \frac{7^2}{2!} + 1= \frac{51}{2}[/latex][/quote]

hm... ja dobio vrlo slično, ali neisto. :? :bbunny:
[latex]a_n = \left\{ \begin{array}{rcl} 0, & n=0 \\ \frac{17}{2}, & n=2 \\ \frac{7^{n-1}}{(n-1)!}, & n \neq 0, & n \neq 2 \end{array}\right.[/latex]

:cowdance:
Luuka (napisa):
A 2.b je:




hm... ja dobio vrlo slično, ali neisto. Confused Blue bunny


Plesuca krava



_________________
ima let u finish
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 2. godine -> Diskretna matematika Vremenska zona: GMT + 01:00.
Stranica 1 / 1.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan