| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
blob
Forumaš(ica)


Pridružen/a: 13. 07. 2007. (18:09:52)
Postovi: (23)16
|
 Postano: 8:40 čet, 3. 1. 2008 Naslov: Monotonost niza, samo hint u vezi DZ Postano: 8:40 čet, 3. 1. 2008 Naslov: Monotonost niza, samo hint u vezi DZ |
    |
|
|
Zadatak glasi: ispitajte monotonost sljedećeg niza: [latex]b_n=\frac{
\sqrt{n^2+1}-n}
{\sqrt{n+3}+2n}[/latex].
Prvih par članova je [latex]b_1=\frac{\sqrt{2}-1}{4} \approx 0.1036,
b_2=\frac{\sqrt{5}-2}{\sqrt{5}+4} \approx 0.0379[/latex],
pa ako npr. krenem rješavati indukcijom, trebam dokazati da je niz padajuć, tj, da je [latex]b_n \geq b_{n+1}, \forall n \in \mathbb{N}[/latex].
Baza je OK, iz gornjega se vidi da je [latex]b_1 \geq b_2[/latex].
Pretpostavimo da za neki [latex]n \in \mathbb{N}[/latex] vrijedi [latex]b_n \geq b_{n+1}[/latex].
I sad treba vidjeti je li istinita tvrdnja [latex]b_{n+1} \geq b_{n+2}[/latex], tj. [latex]\frac{\sqrt{(n+1)^2+1}-(n+1)}
{\sqrt{(n+1)+3}+2(n+1)}\geq
\frac{\sqrt{(n+2)^2+1}-(n+2)}
{\sqrt{(n+2)+3}+2(n+2)}[/latex] :blueshock: :yikes:
Evo, tu mi treba hint. Pokušavao sam ovaj izraz kvadrirati, ili množiti nazivnicima itd. no nikako ga nisam uspijevao srediti, a sigurno se za čas može riješiti. :)
***
S druge strane, je li u redu /legitimno ići "zaobilaznim" putem, ako primijetimo da je lijevi broj sigurno veći od desnoga ako je brojnik lijevoga veći od brojnika desnoga, a nazivnik lijevoga manji od nazivnika desnoga, tj. [latex] (a \geq c)\& (b \leq d) \Rightarrow \frac{a}{b} \geq \frac{c}{d}[/latex]?
Jer onda, uvrštavanjem odgovarajućih dijelova u taj izraz, promatramo odnose:
[latex]\sqrt{(n+1)^2+1}-(n+1) \geq \sqrt{(n+2)^2+1}-(n+2)[/latex], odnosno
[latex]\sqrt{(n+1)+3}+2(n+1) \leq \sqrt{(n+2)+3}+2(n+2)[/latex], iz čega nakon sređivanja slijedi
[latex]n^2+4n+1 \geq 0[/latex], što je očito istina za svaki [latex]n \in \mathbb{N}[/latex], odnosno
[latex]4 \sqrt{n+5} \geq -5[/latex], što također vrijedi svaki [latex]n \in \mathbb{N}[/latex], pa je dokaz indukcijom gotov (ne?) i zaključujemo kako je, zbog istinitosti [latex]b_{n+1} \geq b_{n+2}[/latex], niz [latex](b_n)[/latex] padajuć...
Zahvaljujem :naklon:
Zadatak glasi: ispitajte monotonost sljedećeg niza: 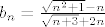 . .
Prvih par članova je 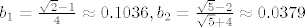 , ,
pa ako npr. krenem rješavati indukcijom, trebam dokazati da je niz padajuć, tj, da je 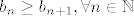 . .
Baza je OK, iz gornjega se vidi da je 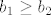 . .
Pretpostavimo da za neki  vrijedi vrijedi 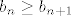 . .
I sad treba vidjeti je li istinita tvrdnja 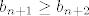 , tj. , tj. 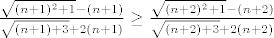  
Evo, tu mi treba hint. Pokušavao sam ovaj izraz kvadrirati, ili množiti nazivnicima itd. no nikako ga nisam uspijevao srediti, a sigurno se za čas može riješiti. 
***
S druge strane, je li u redu /legitimno ići "zaobilaznim" putem, ako primijetimo da je lijevi broj sigurno veći od desnoga ako je brojnik lijevoga veći od brojnika desnoga, a nazivnik lijevoga manji od nazivnika desnoga, tj. 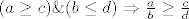 ? ?
Jer onda, uvrštavanjem odgovarajućih dijelova u taj izraz, promatramo odnose:
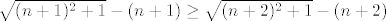 , odnosno , odnosno
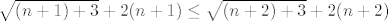 , iz čega nakon sređivanja slijedi , iz čega nakon sređivanja slijedi
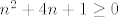 , što je očito istina za svaki , što je očito istina za svaki  , odnosno , odnosno
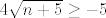 , što također vrijedi svaki , što također vrijedi svaki  , pa je dokaz indukcijom gotov (ne?) i zaključujemo kako je, zbog istinitosti , pa je dokaz indukcijom gotov (ne?) i zaključujemo kako je, zbog istinitosti 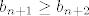 , niz , niz 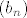 padajuć... padajuć...
Zahvaljujem 
Zadnja promjena: blob; 21:15 čet, 3. 1. 2008; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
blob
Forumaš(ica)


Pridružen/a: 13. 07. 2007. (18:09:52)
Postovi: (23)16
|
 Postano: 11:19 čet, 3. 1. 2008 Naslov: Postano: 11:19 čet, 3. 1. 2008 Naslov: |
    |
|
|
[quote="Masiela"]Počela sam pisati taj domaći :roll:
Stavila sam to s brojnicima i nazivnicima što pitaš je li legitimno.[/quote]
Taj način (raščlambom, rastavljanjem) je valjda OK, no možda postoji neki superelegantan trik za onu gore nejednakost, tipa: nešto se doda i oduzme, tu s nečim pomnožiš, tamo podijeliš i cap! :disappear: u trenu evo izraza tipa [latex]
n^2 \geq 0 [/latex] :D
| Masiela (napisa): | Počela sam pisati taj domaći 
Stavila sam to s brojnicima i nazivnicima što pitaš je li legitimno. |
Taj način (raščlambom, rastavljanjem) je valjda OK, no možda postoji neki superelegantan trik za onu gore nejednakost, tipa: nešto se doda i oduzme, tu s nečim pomnožiš, tamo podijeliš i cap!  u trenu evo izraza tipa u trenu evo izraza tipa  
|
|
| [Vrh] |
|
felixx
Forumaš(ica)

Pridružen/a: 27. 11. 2007. (15:31:43)
Postovi: (61)16
Lokacija: *obrisano*
|
|
| [Vrh] |
|
blob
Forumaš(ica)


Pridružen/a: 13. 07. 2007. (18:09:52)
Postovi: (23)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 15:38 čet, 3. 1. 2008 Naslov: Re: Monotonost niza, samo hint u vezi DZ Postano: 15:38 čet, 3. 1. 2008 Naslov: Re: Monotonost niza, samo hint u vezi DZ |
    |
|
|
[quote="blob"]S druge strane, je li u redu /legitimno ići "zaobilaznim" putem, ako primijetimo da je lijevi broj sigurno veći od desnoga akko je brojnik lijevoga veći od brojnika desnoga, a nazivnik lijevoga manji od nazivnika desnoga, tj. [latex]\frac{a}{b} \geq \frac{c}{d} \Leftrightarrow (a \geq c)\& (b \leq d)[/latex]?[/quote]
Ovo jednostavno nije tocno. :ccc:
Tocno je: [latex]\frac{a}{b} \geq \frac{c}{d} \Leftarrow (a \geq c) \& (b \leq d)[/latex] :)
Npr. [latex]\frac57 \geq \frac23 \not\Rightarrow (5 \geq 2) \& (7 \leq 3)[/latex]. ;)
| blob (napisa): | S druge strane, je li u redu /legitimno ići "zaobilaznim" putem, ako primijetimo da je lijevi broj sigurno veći od desnoga akko je brojnik lijevoga veći od brojnika desnoga, a nazivnik lijevoga manji od nazivnika desnoga, tj. 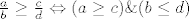 ? ? |
Ovo jednostavno nije tocno. 
Tocno je: 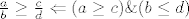 
Npr. 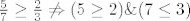 . . 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
felixx
Forumaš(ica)

Pridružen/a: 27. 11. 2007. (15:31:43)
Postovi: (61)16
Lokacija: *obrisano*
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
|








