| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:46 pet, 4. 1. 2008 Naslov: Postano: 21:46 pet, 4. 1. 2008 Naslov: |
    |
|
|
Gle, ima i drugi zadatak! :oops:
Vrijedi:
[latex]m := 1^2+2^2+\dots+n^2 = \frac{n(n + 1)(2n + 1)}6 = \frac{2n^3+3n^2+n}6[/latex]
[latex]M := 2^2+3^2+\dots+(n+1)^2 = \frac{(n+1)((n+1) + 1)(2(n+1) + 1)}6 - 1 = \frac{2(n+1)^3+3(n+1)^2+(n+1) - 6}6[/latex]
E, onda pokazes da je tvoja suma izmedju m i M koji imaju isto uz n^3, a ostatak nije bitan za limes (to isto pokazes). :)
Gle, ima i drugi zadatak! 
Vrijedi:
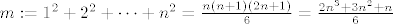
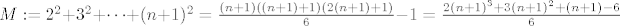
E, onda pokazes da je tvoja suma izmedju m i M koji imaju isto uz n^3, a ostatak nije bitan za limes (to isto pokazes). 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 1:45 sub, 5. 1. 2008 Naslov: Postano: 1:45 sub, 5. 1. 2008 Naslov: |
    |
|
|
[quote="lucika"]otkud m=(n(n+1)(2n+1)) / 6 ??? to neka formula? :-k[/quote]
Yup: suma kvadrata prvih [i]n[/i] prirodnih brojeva. :D
Jasno, ja to ne znam na pamet, pa sam iskopao s [url=http://en.wikipedia.org/wiki/Square_(algebra)]Wikipedije[/url]. :oops:
[quote="lucika"]jel se onda taj zadatak rješava prek teorema o sendviču?[/quote]
Mislim da je to taj teorem (u mojim godinama, nazivlje teorema koji su van mog podrucja malo izblijedi iz sjecanja :oops:).
[quote="lucika"]btw: kak da sve ove matematičke izraze napišem ovak lijepo ko ti a ne s petsto zagradica? :?[/quote]
Dovuci misa iznad [img]http://degiorgi.math.hr/forum/templates/Classic/images/icon_plainpreview.gif[/img] ili pikni na "citiraj" ("quote" ako koristis englesku shemu), pa ces vidjeti kako sam ja to slozio. 8)
Osnovno je objasnjeno [url=http://degiorgi.math.hr/forum/viewtopic.php?t=2474]ovdje[/url], a konkretnu upotrebu vidis iz postova onih koji to koriste ili iz literature koja je navedena u samom topicu koji ti polinkah. :)
| lucika (napisa): | otkud m=(n(n+1)(2n+1)) / 6 ??? to neka formula?  |
Yup: suma kvadrata prvih n prirodnih brojeva. 
Jasno, ja to ne znam na pamet, pa sam iskopao s Wikipedije. 
| lucika (napisa): | | jel se onda taj zadatak rješava prek teorema o sendviču? |
Mislim da je to taj teorem (u mojim godinama, nazivlje teorema koji su van mog podrucja malo izblijedi iz sjecanja  ). ).
| lucika (napisa): | btw: kak da sve ove matematičke izraze napišem ovak lijepo ko ti a ne s petsto zagradica?  |
Dovuci misa iznad  ili pikni na "citiraj" ("quote" ako koristis englesku shemu), pa ces vidjeti kako sam ja to slozio. ili pikni na "citiraj" ("quote" ako koristis englesku shemu), pa ces vidjeti kako sam ja to slozio. 
Osnovno je objasnjeno ovdje, a konkretnu upotrebu vidis iz postova onih koji to koriste ili iz literature koja je navedena u samom topicu koji ti polinkah. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 22:26 sub, 5. 1. 2008 Naslov: Postano: 22:26 sub, 5. 1. 2008 Naslov: |
    |
|
|
[quote="Atomised"][quote="lucika"]sam još jedno pitanjce:kolko je +beskonačno / (1+(+beskonačno))?jel to uopće izračunjivo? :?[/quote]
Nije definirano. ;)[/quote]
Tocno tako, dok se ne zna odakle su te beskonacnosti. :D Primjeri:
[latex]\lim\limits_{x\to\infty}\frac{x}{1+x^2} = 0[/latex]
[latex]\lim\limits_{x\to\infty}\frac{ax}{1+x} = a[/latex]
[latex]\lim\limits_{x\to\infty}\frac{x^2}{1+x} = \infty[/latex]
Ocito, ovisno o parametru [i]a[/i] > 0, moze se nastimati da rezultat od "+beskonačno / (1+(+beskonačno))" bude bilo koji nenegativni realni broj. :)
[quote="Atomised"]@vsego: Ne može li se u tu formulu za zbroj prvih n kvadrata prirodnih brojeva jednostavno umjesto n uvrstiti n - 1, pa ni ne koristiti tm. o sendviču?[/quote]
Mozda i moze, ali bas ne pratim tvoju ideju. :oops: Raspisi, pa cemo vidjeti. 8)
| Atomised (napisa): | | lucika (napisa): | sam još jedno pitanjce:kolko je +beskonačno / (1+(+beskonačno))?jel to uopće izračunjivo?  |
Nije definirano.  |
Tocno tako, dok se ne zna odakle su te beskonacnosti.  Primjeri: Primjeri:
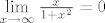
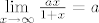
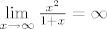
Ocito, ovisno o parametru a > 0, moze se nastimati da rezultat od "+beskonačno / (1+(+beskonačno))" bude bilo koji nenegativni realni broj. 
| Atomised (napisa): | | @vsego: Ne može li se u tu formulu za zbroj prvih n kvadrata prirodnih brojeva jednostavno umjesto n uvrstiti n - 1, pa ni ne koristiti tm. o sendviču? |
Mozda i moze, ali bas ne pratim tvoju ideju.  Raspisi, pa cemo vidjeti. Raspisi, pa cemo vidjeti. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
|














