| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mala
Forumaš(ica)


Pridružen/a: 10. 10. 2006. (16:13:20)
Postovi: (2A)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
petrat
Forumaš s poteškoćama u pisanju

Pridružen/a: 20. 12. 2005. (10:23:20)
Postovi: (33)16
|
|
| [Vrh] |
|
MKova
Forumaš(ica)

Pridružen/a: 01. 10. 2005. (18:24:38)
Postovi: (187)16
Spol: 
|
|
| [Vrh] |
|
Feanor
Forumaš(ica)

Pridružen/a: 15. 11. 2005. (18:18:15)
Postovi: (27)16
Spol: 
Lokacija: Zagreb/Bjelovar
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Feanor
Forumaš(ica)

Pridružen/a: 15. 11. 2005. (18:18:15)
Postovi: (27)16
Spol: 
Lokacija: Zagreb/Bjelovar
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:20 ned, 10. 2. 2008 Naslov: Postano: 18:20 ned, 10. 2. 2008 Naslov: |
    |
|
|
3. zadatak? Pomoć... probo sam pretp suprotno pa koristio teorem da je p-q+r=2 i onu staru formulu da je 2q=suma stupnjeva vrhova pa da dobijem neku kontradikciju ali nejde...
3. zadatak? Pomoć... probo sam pretp suprotno pa koristio teorem da je p-q+r=2 i onu staru formulu da je 2q=suma stupnjeva vrhova pa da dobijem neku kontradikciju ali nejde...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
MKova
Forumaš(ica)

Pridružen/a: 01. 10. 2005. (18:24:38)
Postovi: (187)16
Spol: 
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
jelena
Forumaš(ica)

Pridružen/a: 06. 08. 2005. (17:08:55)
Postovi: (18)16
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)

Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: 
Lokacija: Scranton
|
|
| [Vrh] |
|
Feanor
Forumaš(ica)

Pridružen/a: 15. 11. 2005. (18:18:15)
Postovi: (27)16
Spol: 
Lokacija: Zagreb/Bjelovar
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 1:30 čet, 14. 2. 2008 Naslov: Postano: 1:30 čet, 14. 2. 2008 Naslov: |
    |
|
|
[quote="napraviculom"]sta je s ovim drugim grafom u zad 5? su vrhovi u svim sjecistima :) , samo na kruznici ili kako?[/quote]
Ni meni bas nije bilo jasno, pa sam poslao mail asis. Tadić koja je odgovorila (poprilično brzo, tnx :)) da su vrhovi samo oni na kružnici.
[quote="jelena"]da li je netko mozda rijesio ova dva zadatka?
6. Neka je v(G)>=11. dokažite G ili Gkomplement mora biti neplanaran.[/quote]
Pretp. oba [latex]G,G^{C}[/latex] planarni. [latex]n:=|V(G)|=|V(G^{C})|[/latex]
Iz definicije komplementa imamo [latex]|E(G)|+|E(G^{C})|=|E(K_{n})|={n \choose 2}[/latex] , a zbog, u prošlom postu spomenutog zadatka, vrijedi
[latex]|E(G)|,|E(G^{C})| \leq 3n-6 \ \ \Rightarrow \ \ {n \choose 2} \leq 2(3n-6) \ \ \Rightarrow \ \ n^{2}-11n+24 \leq 0[/latex] . Sad još treba samo pokazati da ta nejednakost nije nikad istinita za [latex]n \geq 11[/latex] , a to znamo 8)
Evo, kad sam se već uživia
[quote="jelena"]7.Koliko jednostavni graf s n vrhova mora imati bridova da bi smo bili sigurni da nije bipartitan?[/quote]
Ovako ide moja ocjena. G sigurno nije bipartitan ako ima više vrhova od svakog potpunog bipartitog grafa [latex]K_{i,n-i} \ \forall i=1..n[/latex]
[latex]|E(K_{i,n-i})|=i(n-i)=-i^{2}-ni[/latex], i tražimo maximum te funkcije u ovisnosti o i. Vidi se pa je to parabola okrenuta prema dolje, s nultočkama u 0,n, pa je maximum na sredini, u n\2. Znači graf mora imati strogo više od [latex] \ -( \frac{n}{2})^{2}+n \spot \frac{n}{2}= \frac{n^{2}}{4}
[/latex] bridova, da sigurno ne bude bipartitan.
Da je to "najbolja" ocjena, vidi se još i iz primjera. Za n=4, e=4 možemo složiti bipartitan graf.
| napraviculom (napisa): | sta je s ovim drugim grafom u zad 5? su vrhovi u svim sjecistima  , samo na kruznici ili kako? , samo na kruznici ili kako? |
Ni meni bas nije bilo jasno, pa sam poslao mail asis. Tadić koja je odgovorila (poprilično brzo, tnx  ) da su vrhovi samo oni na kružnici. ) da su vrhovi samo oni na kružnici.
| jelena (napisa): | da li je netko mozda rijesio ova dva zadatka?
6. Neka je v(G)>=11. dokažite G ili Gkomplement mora biti neplanaran. |
Pretp. oba 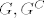 planarni. planarni. 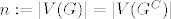
Iz definicije komplementa imamo 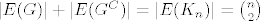 , a zbog, u prošlom postu spomenutog zadatka, vrijedi , a zbog, u prošlom postu spomenutog zadatka, vrijedi
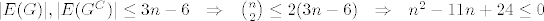 . Sad još treba samo pokazati da ta nejednakost nije nikad istinita za . Sad još treba samo pokazati da ta nejednakost nije nikad istinita za  , a to znamo , a to znamo 
Evo, kad sam se već uživia
| jelena (napisa): | | 7.Koliko jednostavni graf s n vrhova mora imati bridova da bi smo bili sigurni da nije bipartitan? |
Ovako ide moja ocjena. G sigurno nije bipartitan ako ima više vrhova od svakog potpunog bipartitog grafa 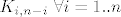
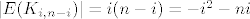 , i tražimo maximum te funkcije u ovisnosti o i. Vidi se pa je to parabola okrenuta prema dolje, s nultočkama u 0,n, pa je maximum na sredini, u n\2. Znači graf mora imati strogo više od , i tražimo maximum te funkcije u ovisnosti o i. Vidi se pa je to parabola okrenuta prema dolje, s nultočkama u 0,n, pa je maximum na sredini, u n\2. Znači graf mora imati strogo više od 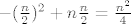 bridova, da sigurno ne bude bipartitan. bridova, da sigurno ne bude bipartitan.
Da je to "najbolja" ocjena, vidi se još i iz primjera. Za n=4, e=4 možemo složiti bipartitan graf.
_________________
Rafael Mrđen
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 11:47 čet, 14. 2. 2008 Naslov: Postano: 11:47 čet, 14. 2. 2008 Naslov: |
    |
|
|
U 5. zadatku u prvom grafu slijeva su vrhovi u vrhovima vanjskog peterokuta i u vrhovima zvijezde koja je unutra ?
U 5. zadatku u prvom grafu slijeva su vrhovi u vrhovima vanjskog peterokuta i u vrhovima zvijezde koja je unutra ?
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
napraviculom
Forumaš(ica)

Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: 
Lokacija: Scranton
|
 Postano: 12:47 čet, 14. 2. 2008 Naslov: Postano: 12:47 čet, 14. 2. 2008 Naslov: |
    |
|
|
[quote="Luuka"]U 5. zadatku u prvom grafu slijeva su vrhovi u vrhovima vanjskog peterokuta i u vrhovima zvijezde koja je unutra ?[/quote]
mislim da da, to je onaj Petersenov kojeg smo spomenuli na predavanjima
da ne otvaram novi post:
U dokazu korolara : [i]Graf je stablo <=> ne sadrzi cikluse, ali dodavanjem bilo kojeg novog brida dobijemo ciklus[/i]
=>
Po def stablo ne sadrzi cikluse
Je li dovoljno reci: dodavanjem brida u G nismo izgubili svojstvo povezanosti, ali smo izgubili svojstvo stabla (zbog br. bridova) i onda iz toga zakljuciti da je to zbog postojanja ciklusa?
Ili onda jos pokazati da postoji ciklus (pretpostaviti suprotno, tj. da ne postoji =>izbacivanjem se rusi povezanost, izbacimo onaj isti e, nismo izgubili povezanost – kontradikcija => postoji ciklus)
| Luuka (napisa): | | U 5. zadatku u prvom grafu slijeva su vrhovi u vrhovima vanjskog peterokuta i u vrhovima zvijezde koja je unutra ? |
mislim da da, to je onaj Petersenov kojeg smo spomenuli na predavanjima
da ne otvaram novi post:
U dokazu korolara : Graf je stablo ⇔ ne sadrzi cikluse, ali dodavanjem bilo kojeg novog brida dobijemo ciklus
⇒
Po def stablo ne sadrzi cikluse
Je li dovoljno reci: dodavanjem brida u G nismo izgubili svojstvo povezanosti, ali smo izgubili svojstvo stabla (zbog br. bridova) i onda iz toga zakljuciti da je to zbog postojanja ciklusa?
Ili onda jos pokazati da postoji ciklus (pretpostaviti suprotno, tj. da ne postoji ⇒izbacivanjem se rusi povezanost, izbacimo onaj isti e, nismo izgubili povezanost – kontradikcija ⇒ postoji ciklus)
_________________
"I'm the operator with my pocket calculator"
|
|
| [Vrh] |
|
|






















