| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
1191213220
Forumaš(ica)

Pridružen/a: 19. 07. 2007. (15:10:13)
Postovi: (16)16
Spol: 
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
ivica13
Forumaš(ica)

Pridružen/a: 03. 10. 2007. (14:01:02)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
1191213220
Forumaš(ica)

Pridružen/a: 19. 07. 2007. (15:10:13)
Postovi: (16)16
Spol: 
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
ivica13
Forumaš(ica)

Pridružen/a: 03. 10. 2007. (14:01:02)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
1191213220
Forumaš(ica)

Pridružen/a: 19. 07. 2007. (15:10:13)
Postovi: (16)16
Spol: 
|
|
| [Vrh] |
|
1191213220
Forumaš(ica)

Pridružen/a: 19. 07. 2007. (15:10:13)
Postovi: (16)16
Spol: 
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
ivica13
Forumaš(ica)

Pridružen/a: 03. 10. 2007. (14:01:02)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 11:26 sri, 6. 2. 2008 Naslov: Postano: 11:26 sri, 6. 2. 2008 Naslov: |
    |
|
|
[quote="1191213220"]
[b][u]Ispravak[/u]
k=2, a to smo uzeli iz onog prvog f(x), tj. f(2)[/b]
(malo sam zamjenila slova f i p, tak da me ispričajte, gdje je f mozete napisat p)
[b]Alfa - k | g(x) slijedi 6-2|f(2) dakle 4|-2
Prema tome [u]NE[/u] postoji p s cjelobrojnim koeficjentima![/b][/quote]
Moram priznat da mi baš nije najjasnije...
[latex]p(2)=4,\ p(6)=6[/latex]
Definiramo:
[latex]g(x)=p(x)-6\Rightarrow g(6)=0[/latex]
I sad veliš da po teoremu:
[latex]\alpha-k|f(k)[/latex], gdje je [latex]\alpha[/latex] nultočka od f, dobijemo:
[latex]\alpha-k|g(k)\Rightarrow 6-2|g(2)\Rightarrow 4|p(2)-6\Rightarrow 4|-2[/latex]
AAA.... Ok... Sad kad sam si ovako raspisao sam shvatio. :)
Ostaviti ću svejedno reply, možda pomogne nekome još...
| 1191213220 (napisa): |
Ispravak
k=2, a to smo uzeli iz onog prvog f(x), tj. f(2)
(malo sam zamjenila slova f i p, tak da me ispričajte, gdje je f mozete napisat p)
Alfa - k | g(x) slijedi 6-2|f(2) dakle 4|-2
Prema tome NE postoji p s cjelobrojnim koeficjentima! |
Moram priznat da mi baš nije najjasnije...
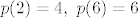
Definiramo:
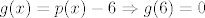
I sad veliš da po teoremu:
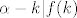 , gdje je , gdje je  nultočka od f, dobijemo: nultočka od f, dobijemo:
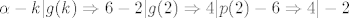
AAA.... Ok... Sad kad sam si ovako raspisao sam shvatio. 
Ostaviti ću svejedno reply, možda pomogne nekome još...
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
k8yvis
Forumaš(ica)

Pridružen/a: 13. 10. 2006. (14:32:30)
Postovi: (79)16
Spol: 
|
|
| [Vrh] |
|
mocibob
Forumaš(ica)

Pridružen/a: 08. 03. 2007. (10:26:53)
Postovi: (16)16
|
 Postano: 16:06 sri, 6. 2. 2008 Naslov: 8. zadatak.. Postano: 16:06 sri, 6. 2. 2008 Naslov: 8. zadatak.. |
    |
|
|
ne razumijem bas sto se trazi u zadatku.... :oops: ...npr., pod a), trebam taj polinom podijelit s x-1 pomocu hornera, ili??
za neupucene, zad. glasi ovako: "Primjenom Hornerovog algoritma razvijte polinom f(x) po potencijama polinoma (x-a), ako je: a) f(x)= 3x^3-11x^2+ 14x+4... a=1...
hvaaala..
ne razumijem bas sto se trazi u zadatku....  ...npr., pod a), trebam taj polinom podijelit s x-1 pomocu hornera, ili?? ...npr., pod a), trebam taj polinom podijelit s x-1 pomocu hornera, ili??
za neupucene, zad. glasi ovako: "Primjenom Hornerovog algoritma razvijte polinom f(x) po potencijama polinoma (x-a), ako je: a) f(x)= 3x^3-11x^2+ 14x+4... a=1...
hvaaala..
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
k8yvis
Forumaš(ica)

Pridružen/a: 13. 10. 2006. (14:32:30)
Postovi: (79)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 17:32 sri, 6. 2. 2008 Naslov: Postano: 17:32 sri, 6. 2. 2008 Naslov: |
    |
|
|
[quote="punio4"]No zapeo sam na trećem... Može pomoć :) ?
Dakle imamo neki polinom oblika:
[latex]f(x)=a_n x^n + a_{n-1}x^{n-1}\ldots+a_1 x + a_0[/latex]
[latex]g(x)=x^2-1[/latex]
I vrijedi iduće:
[latex]a_1+\ldots + a_n = 2[/latex]
[latex]a_1+a_3+\ldots+a_{2n-1}=a_2+a_4+\ldots+a_{2n}[/latex]
Traži se ostatak pri dijeljenju polinoma, [latex]r(x)[/latex].[/quote]
ne treba ti horner :P
to ti je super primjer za ono što si pitao - gdje nam pomažu nultočke polinoma kojim dijelimo :D
imaš: [latex]f(x) = q(x) \cdot g(x) + r(x)[/latex].
sada lijepo uvrstiš nultočke od g u jednadžbu - time ćeš ubiti q(x) (polinom koji smo dobili dijeljenjem f sa g, a koji ne znamo, niti trebamo znati). s obzirom da su nultočke od g tako lijepe, koristeći dodatne jednakosti iz zadatka dobit ćeš čemu je jednak ostatak (on je, za početak, polinom najviše stupnja 1). :wink:
:rakun:
| punio4 (napisa): | No zapeo sam na trećem... Može pomoć  ? ?
Dakle imamo neki polinom oblika:
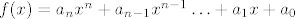
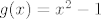
I vrijedi iduće:

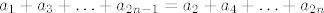
Traži se ostatak pri dijeljenju polinoma, 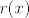 . . |
ne treba ti horner 
to ti je super primjer za ono što si pitao - gdje nam pomažu nultočke polinoma kojim dijelimo 
imaš: 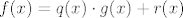 . .
sada lijepo uvrstiš nultočke od g u jednadžbu - time ćeš ubiti q(x) (polinom koji smo dobili dijeljenjem f sa g, a koji ne znamo, niti trebamo znati). s obzirom da su nultočke od g tako lijepe, koristeći dodatne jednakosti iz zadatka dobit ćeš čemu je jednak ostatak (on je, za početak, polinom najviše stupnja 1). 
_________________
ima let u finish
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
 Postano: 17:43 sri, 6. 2. 2008 Naslov: Re: 8. zadatak.. Postano: 17:43 sri, 6. 2. 2008 Naslov: Re: 8. zadatak.. |
    |
|
|
[quote="mocibob"]ne razumijem bas sto se trazi u zadatku.... :oops: ...npr., pod a), trebam taj polinom podijelit s x-1 pomocu hornera, ili??
za neupucene, zad. glasi ovako: "Primjenom Hornerovog algoritma razvijte polinom f(x) po potencijama polinoma (x-a), ako je: a) f(x)= 3x^3-11x^2+ 14x+4... a=1...
hvaaala..[/quote]
Trebaš napisati taj polinom u obliku f(x) = A(x-1)^3 + B(x-1)^2 + C(x-1) + D, a u tome ti pomaže Hornerov algoritam... Sad, kako se točno to radi imaš možda u bilježnici, a sigurno u onoj Pavković-Veljan knjizi (EM1).
| mocibob (napisa): | ne razumijem bas sto se trazi u zadatku....  ...npr., pod a), trebam taj polinom podijelit s x-1 pomocu hornera, ili?? ...npr., pod a), trebam taj polinom podijelit s x-1 pomocu hornera, ili??
za neupucene, zad. glasi ovako: "Primjenom Hornerovog algoritma razvijte polinom f(x) po potencijama polinoma (x-a), ako je: a) f(x)= 3x^3-11x^2+ 14x+4... a=1...
hvaaala.. |
Trebaš napisati taj polinom u obliku f(x) = A(x-1)^3 + B(x-1)^2 + C(x-1) + D, a u tome ti pomaže Hornerov algoritam... Sad, kako se točno to radi imaš možda u bilježnici, a sigurno u onoj Pavković-Veljan knjizi (EM1).
|
|
| [Vrh] |
|
|


















