| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 14:20 ned, 10. 2. 2008 Naslov: 4. zadaća Postano: 14:20 ned, 10. 2. 2008 Naslov: 4. zadaća |
    |
|
|
Prvi zadatak... Malo mi je sumnjivo, neke jako ružne brojeve dobivam.
Da li je kome još ispalo da je rang matrice = 4, neovisno o [latex]\lambda[/latex]?
Naime, išao sam svoditi na donju trokutastu matricu, i dobio sam:
[latex]\begin{bmatrix}
1 & 4 & 3 & -2 \\
0 & 3 & 4 & 10 \\
0 & 0 & \frac{-3-\lambda}{4} & x \\
0 & 0 & -\frac{1}{3} & y
\end{bmatrix}
[/latex]
Gdje su x i y neki odurni brojevi. (3-15/31 i sl.)
[EDIT]
Zanemari ovo, točan rezultat je niže u topicu :P
Prvi zadatak... Malo mi je sumnjivo, neke jako ružne brojeve dobivam.
Da li je kome još ispalo da je rang matrice = 4, neovisno o  ? ?
Naime, išao sam svoditi na donju trokutastu matricu, i dobio sam:
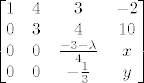
Gdje su x i y neki odurni brojevi. (3-15/31 i sl.)
[EDIT]
Zanemari ovo, točan rezultat je niže u topicu 
Zadnja promjena: punio4; 14:05 uto, 12. 2. 2008; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 16:33 ned, 10. 2. 2008 Naslov: Postano: 16:33 ned, 10. 2. 2008 Naslov: |
    |
|
|
[quote="ma"]hm. pa nije svejedno što su x i y. ako su zadnja dva retka linearno zavisna, onda je rang 3.
[size=4]mislim da to vrijedi samo za [latex]\lambda[/latex]=-11[/size] :wink:
:drooljump:[/quote]
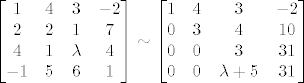
Hm, opet sam riješio, očito sam negdje prije bio fulao... Dakle, dobijem:
[latex]\begin{bmatrix}
1&4&3&-2\\2&2&1&7\\4&1&\lambda&4\\-1&5&6&1\end{bmatrix} \sim
\begin{bmatrix}
1&4&3&-2\\0&3&4&10\\0&0&3&31\\0&0&\lambda+5&31\end{bmatrix}[/latex]
Dakle za [latex]\lambda=-2[/latex] rang je 3, a za [latex]\lambda\ne-2[/latex] rang je 4.
Može li netko potvrditi?
| ma (napisa): | hm. pa nije svejedno što su x i y. ako su zadnja dva retka linearno zavisna, onda je rang 3.
mislim da to vrijedi samo za  =-11 =-11 
 |
Hm, opet sam riješio, očito sam negdje prije bio fulao... Dakle, dobijem:
Dakle za 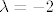 rang je 3, a za rang je 3, a za 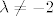 rang je 4. rang je 4.
Može li netko potvrditi?
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:27 ned, 10. 2. 2008 Naslov: Postano: 19:27 ned, 10. 2. 2008 Naslov: |
    |
|
|
[quote="Atomised"]
Kakva su vam rješenja na ostale zadatke?
Drugi sam dva puta rješavao i dobio dva različita rješenja, pa da ne moram i treći put...[/quote]
Drugi ispada:
[latex]A^{-1} = \begin{bmatrix}0&-1&\frac{2}{3}\\-1&0&\frac{2}{3}\\1&1&-1\end{bmatrix}[/latex]
Treći imam neku općenitu ideju, ali ne znam kako se to "veli" matematički.
Za kvadratne reda n i ranga n je trivijalno, a za matrice A=m*n, B=n*k...
Hm... Kako se zove oblik matrice kad ima samo nule i jedinice?
Uglavnom, svedemo A i B na takav oblik, tako da imamo neke "male" jedinične matrice u gornjem lijevom bloku.
Nužno ispada, da na mjestima i=j će rezultat biti jedan, a na i!=j nula.
I rang matrice AB će biti min{r(A), r(B)}
A za četvrti... Ne znam baš te sa parametarskim rješenjima. Kako se to rješava?
Prvo napravimo kvazi-donju trokutastu (kako se zove taj oblik? u Schaumu piše "Echelon Form")... I onda... Pitamo na forumu kako dalje :lol:
| Atomised (napisa): |
Kakva su vam rješenja na ostale zadatke?
Drugi sam dva puta rješavao i dobio dva različita rješenja, pa da ne moram i treći put... |
Drugi ispada:

Treći imam neku općenitu ideju, ali ne znam kako se to "veli" matematički.
Za kvadratne reda n i ranga n je trivijalno, a za matrice A=m*n, B=n*k...
Hm... Kako se zove oblik matrice kad ima samo nule i jedinice?
Uglavnom, svedemo A i B na takav oblik, tako da imamo neke "male" jedinične matrice u gornjem lijevom bloku.
Nužno ispada, da na mjestima i=j će rezultat biti jedan, a na i!=j nula.
I rang matrice AB će biti min{r(A), r(B)}
A za četvrti... Ne znam baš te sa parametarskim rješenjima. Kako se to rješava?
Prvo napravimo kvazi-donju trokutastu (kako se zove taj oblik? u Schaumu piše "Echelon Form")... I onda... Pitamo na forumu kako dalje 
|
|
| [Vrh] |
|
k8yvis
Forumaš(ica)

Pridružen/a: 13. 10. 2006. (14:32:30)
Postovi: (79)16
Spol: 
|
 Postano: 19:56 ned, 10. 2. 2008 Naslov: Postano: 19:56 ned, 10. 2. 2008 Naslov: |
    |
|
|
Šta se tiče determinante poprilično detaljno i ne loše objašnjeno ti piše na osam stranica pdf-a: http://matematika.fkit.hr/novo/matematika%201/predavanja/Mat1_Lekcija4.pdf
A ovo ostalo neznam o čemu se točno radi... :D
Šta se tiče parametarskih riješenja, to ti je kad dobiješ npr: x=3y, y=2z, x=4z, tj, nemaš konkretnih brojeva jer riješenja ovoga je skup brojeva koji zadovoljavaju dane jednakosti.
pozz
Šta se tiče determinante poprilično detaljno i ne loše objašnjeno ti piše na osam stranica pdf-a: http://matematika.fkit.hr/novo/matematika%201/predavanja/Mat1_Lekcija4.pdf
A ovo ostalo neznam o čemu se točno radi... 
Šta se tiče parametarskih riješenja, to ti je kad dobiješ npr: x=3y, y=2z, x=4z, tj, nemaš konkretnih brojeva jer riješenja ovoga je skup brojeva koji zadovoljavaju dane jednakosti.
pozz
_________________
Da li je napredak kad ljudozder uzme vilicu?
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 20:29 ned, 10. 2. 2008 Naslov: Postano: 20:29 ned, 10. 2. 2008 Naslov: |
    |
|
|
[quote="k8yvis"]Šta se tiče determinante poprilično detaljno i ne loše objašnjeno ti piše na osam stranica pdf-a: http://matematika.fkit.hr/novo/matematika%201/predavanja/Mat1_Lekcija4.pdf
A ovo ostalo neznam o čemu se točno radi... :D
Šta se tiče parametarskih riješenja, to ti je kad dobiješ npr: x=3y, y=2z, x=4z, tj, nemaš konkretnih brojeva jer riješenja ovoga je skup brojeva koji zadovoljavaju dane jednakosti.
pozz[/quote]
Tu ništa ne piše o povezanosti ranga matrice sa determinantom.
Jedino što ih povezuje je da ako je r(A) != od stupnja kvadratne matrice A, da je determinanta = 0, iz očitih razloga, ima nulu na dijagonali.
No to ništa ne pomaže za riještiti zadatak iz ranga pomoću determinante, štoviše, ne pada mi na pamet kako bi se moglo uopće, bez da reduciraš na trokutasti oblik, no tu ti ne treba determinanta da vidiš rang :roll:
| k8yvis (napisa): | Šta se tiče determinante poprilično detaljno i ne loše objašnjeno ti piše na osam stranica pdf-a: http://matematika.fkit.hr/novo/matematika%201/predavanja/Mat1_Lekcija4.pdf
A ovo ostalo neznam o čemu se točno radi... 
Šta se tiče parametarskih riješenja, to ti je kad dobiješ npr: x=3y, y=2z, x=4z, tj, nemaš konkretnih brojeva jer riješenja ovoga je skup brojeva koji zadovoljavaju dane jednakosti.
pozz |
Tu ništa ne piše o povezanosti ranga matrice sa determinantom.
Jedino što ih povezuje je da ako je r(A) != od stupnja kvadratne matrice A, da je determinanta = 0, iz očitih razloga, ima nulu na dijagonali.
No to ništa ne pomaže za riještiti zadatak iz ranga pomoću determinante, štoviše, ne pada mi na pamet kako bi se moglo uopće, bez da reduciraš na trokutasti oblik, no tu ti ne treba determinanta da vidiš rang 
|
|
| [Vrh] |
|
ß
Forumaš(ica)
Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
 Postano: 21:41 ned, 10. 2. 2008 Naslov: Postano: 21:41 ned, 10. 2. 2008 Naslov: |
    |
|
|
[quote="punio4"]Jedino što ih povezuje je da ako je r(A) != od stupnja kvadratne matrice A, da je determinanta = 0, iz očitih razloga, ima nulu na dijagonali.
No to ništa ne pomaže za riještiti zadatak iz ranga pomoću determinante, štoviše, ne pada mi na pamet kako bi se moglo uopće, bez da reduciraš na trokutasti oblik, no tu ti ne treba determinanta da vidiš rang :roll:[/quote]
Sorry ako griješim (neka me netko ispravi onda :D ) ali mislim ovako:
Matrica (kvadratna, ofc) ima puni rang akko joj je determinanta različita od nule. To u zadatku gore možeš primjeniti, ako uz malo sređivanja raspišeš determinantu matrice u ovisnosti o parametru lambda.
Naravno, ovo pomaže samo da vidiš da li je matrica stupnja konkretno 4, a kako vidim da za neke vrijednosti od lambda jest tako, možeš to onda i provjeriti.
Vjerojatno ima još neka fora za točnije određivanje kad je rang<n ali se ne mogu sjetiti. :neutral:
| punio4 (napisa): | Jedino što ih povezuje je da ako je r(A) != od stupnja kvadratne matrice A, da je determinanta = 0, iz očitih razloga, ima nulu na dijagonali.
No to ništa ne pomaže za riještiti zadatak iz ranga pomoću determinante, štoviše, ne pada mi na pamet kako bi se moglo uopće, bez da reduciraš na trokutasti oblik, no tu ti ne treba determinanta da vidiš rang  |
Sorry ako griješim (neka me netko ispravi onda  ) ali mislim ovako: ) ali mislim ovako:
Matrica (kvadratna, ofc) ima puni rang akko joj je determinanta različita od nule. To u zadatku gore možeš primjeniti, ako uz malo sređivanja raspišeš determinantu matrice u ovisnosti o parametru lambda.
Naravno, ovo pomaže samo da vidiš da li je matrica stupnja konkretno 4, a kako vidim da za neke vrijednosti od lambda jest tako, možeš to onda i provjeriti.
Vjerojatno ima još neka fora za točnije određivanje kad je rang<n ali se ne mogu sjetiti. 
_________________
Devious movements in your eyes moved me from relief
Breath comes out white clouds with your lies
and filters through me
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 21:44 ned, 10. 2. 2008 Naslov: Postano: 21:44 ned, 10. 2. 2008 Naslov: |
    |
|
|
[quote]Matrica (kvadratna, ofc) ima puni rang akko joj je determinanta različita od nule. To u zadatku gore možeš primjeniti, ako uz malo sređivanja raspišeš determinantu matrice u ovisnosti o parametru lambda.[/quote]
Fora je da središ matricu da možeš računati determinantu, osim ako ne želiš ići po laplaceu :roll:, ili po definiciji :shock: je da svedeš na trokutasti oblik.
A onda se već na kilometar vidi rang, te je bilo kakva determinanta tu redudantna.
| Citat: | | Matrica (kvadratna, ofc) ima puni rang akko joj je determinanta različita od nule. To u zadatku gore možeš primjeniti, ako uz malo sređivanja raspišeš determinantu matrice u ovisnosti o parametru lambda. |
Fora je da središ matricu da možeš računati determinantu, osim ako ne želiš ići po laplaceu  , ili po definiciji , ili po definiciji  je da svedeš na trokutasti oblik. je da svedeš na trokutasti oblik.
A onda se već na kilometar vidi rang, te je bilo kakva determinanta tu redudantna.
|
|
| [Vrh] |
|
ß
Forumaš(ica)

Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
 Postano: 21:53 ned, 10. 2. 2008 Naslov: Postano: 21:53 ned, 10. 2. 2008 Naslov: |
    |
|
|
[quote="punio4"][quote]Matrica (kvadratna, ofc) ima puni rang akko joj je determinanta različita od nule. To u zadatku gore možeš primjeniti, ako uz malo sređivanja raspišeš determinantu matrice u ovisnosti o parametru lambda.[/quote]
Fora je da središ matricu da možeš računati determinantu, osim ako ne želiš ići po laplaceu :roll:, ili po definiciji :shock: je da svedeš na trokutasti oblik.
A onda se već na kilometar vidi rang, te je bilo kakva determinanta tu redudantna.[/quote]
Hmmm.. a ne znam onda na sto se tocno cilja. :(
| punio4 (napisa): | | Citat: | | Matrica (kvadratna, ofc) ima puni rang akko joj je determinanta različita od nule. To u zadatku gore možeš primjeniti, ako uz malo sređivanja raspišeš determinantu matrice u ovisnosti o parametru lambda. |
Fora je da središ matricu da možeš računati determinantu, osim ako ne želiš ići po laplaceu  , ili po definiciji , ili po definiciji  je da svedeš na trokutasti oblik. je da svedeš na trokutasti oblik.
A onda se već na kilometar vidi rang, te je bilo kakva determinanta tu redudantna. |
Hmmm.. a ne znam onda na sto se tocno cilja. 
_________________
Devious movements in your eyes moved me from relief
Breath comes out white clouds with your lies
and filters through me
|
|
| [Vrh] |
|
Gost
|
 Postano: 5:39 pon, 11. 2. 2008 Naslov: Postano: 5:39 pon, 11. 2. 2008 Naslov: |
    |
|
|
Ciljao sam na to da često (pa i u tom zadatku) možeš malo "ležernijim" računanjem vidjeti kada je determinanta jednaka 0 i tada, ekvivalentno, rang manji od maksimalnog. U zadanoj matrici parametar lambda javlja se samo na jednom mjestu pa će vrijednost determinante biti linearna po lambda (L), oblika aL + b i lako je razlikovati slučajeve.
Dakle, iako je determinanta "redundantna" (kako lijepa i jednostavna riječ, ali OK za jezične vježbe: ponavljati uzastopce "determinanta redundantna, determinanta redundantna, determinanta redundantna..." :) ), nije loše za provjeru npr. kad se dobiju "odurni brojevi" možebitno pogrešnim računom.
Zapravo može biti još korisnije u zadacima sličnog tipa kad se parametar poput lambda (ili čak više parametara) pojavljuje na više mjesta u matrici pa se kod svođenja na trokutasti oblik (radi ranga) mogu pojaviti i dosta nezgodni izrazi, dok npr. Laplace (koji jest katkad naporan) ovdje može prilično lako dovesti do polinoma čije nultočke su nam kritične vrijednosti za rang.
Ciljao sam na to da često (pa i u tom zadatku) možeš malo "ležernijim" računanjem vidjeti kada je determinanta jednaka 0 i tada, ekvivalentno, rang manji od maksimalnog. U zadanoj matrici parametar lambda javlja se samo na jednom mjestu pa će vrijednost determinante biti linearna po lambda (L), oblika aL + b i lako je razlikovati slučajeve.
Dakle, iako je determinanta "redundantna" (kako lijepa i jednostavna riječ, ali OK za jezične vježbe: ponavljati uzastopce "determinanta redundantna, determinanta redundantna, determinanta redundantna..."  ), nije loše za provjeru npr. kad se dobiju "odurni brojevi" možebitno pogrešnim računom. ), nije loše za provjeru npr. kad se dobiju "odurni brojevi" možebitno pogrešnim računom.
Zapravo može biti još korisnije u zadacima sličnog tipa kad se parametar poput lambda (ili čak više parametara) pojavljuje na više mjesta u matrici pa se kod svođenja na trokutasti oblik (radi ranga) mogu pojaviti i dosta nezgodni izrazi, dok npr. Laplace (koji jest katkad naporan) ovdje može prilično lako dovesti do polinoma čije nultočke su nam kritične vrijednosti za rang.
|
|
| [Vrh] |
|
k8yvis
Forumaš(ica)

Pridružen/a: 13. 10. 2006. (14:32:30)
Postovi: (79)16
Spol: 
|
 Postano: 11:04 pon, 11. 2. 2008 Naslov: Postano: 11:04 pon, 11. 2. 2008 Naslov: |
    |
|
|
[quote]Točno je da je rang jednak 3 samo za lambda = -2, inače 4.
Provjereno. Inače, nije loše ovakav zadatak rješavati ili provjeriti
i pomoću determinante.
Erm, kako to napraviti?[/quote]
[quote]A za četvrti... Ne znam baš te sa parametarskim rješenjima. Kako se to rješava?[/quote]
Ja sam odgovarala na ove stavke, ne na zadatak koji, usput rečeno, neznam ni kako izgleda. :?
| Citat: | Točno je da je rang jednak 3 samo za lambda = -2, inače 4.
Provjereno. Inače, nije loše ovakav zadatak rješavati ili provjeriti
i pomoću determinante.
Erm, kako to napraviti? |
| Citat: | | A za četvrti... Ne znam baš te sa parametarskim rješenjima. Kako se to rješava? |
Ja sam odgovarala na ove stavke, ne na zadatak koji, usput rečeno, neznam ni kako izgleda. 
_________________
Da li je napredak kad ljudozder uzme vilicu?
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 14:34 uto, 12. 2. 2008 Naslov: Postano: 14:34 uto, 12. 2. 2008 Naslov: |
    |
|
|
Četvrti zadatak... Sustav 3×5. Evo kaj mathematica veli:
[latex]m=\{\{1,1,1,-1,7\},\{1,-1,-6,0,1\},\{2,1,1,1,0\}\}[/latex]
[latex]\text{LinearSolve}[m, \{2,4,6\}][/latex]
[latex]\text{Out=}\left\{4,-\frac{12}{5},\frac{2}{5},0,0\right\}[/latex]
Ja iskreno nemam pojma kako doći do ovog rješenja.
Četvrti zadatak... Sustav 3×5. Evo kaj mathematica veli:
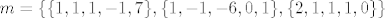
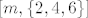
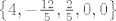
Ja iskreno nemam pojma kako doći do ovog rješenja.
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 15:19 uto, 12. 2. 2008 Naslov: Postano: 15:19 uto, 12. 2. 2008 Naslov: |
    |
|
|
ja sam dobio sljedeće:
[latex](x_1,x_2,x_3,x_4,x_5)=t(-2,4,-1,1,0)+s(-7,18,-4,0,1)+(4,-\frac{12}{5},\frac{2}{5},0,0); \ t, \ s\in\mathbb{R}[/latex]
e sad. ja ne znam šta mathematica izbacuje. očito su i 'oni' uzeli da su [latex]x_4[/latex] i [latex]x_5[/latex] parametri. :? pa se samo ispiše 'pomak'.
uglavnom, jako nam je slično :D
postoji [url=http://wims.unice.fr/wims/wims.cgi?module=tool/linear/linsolver.en]rješavač[/url] koji, doduše, nisam koristio, ali možda će biti od pomoći 8)
ja sam dobio sljedeće:
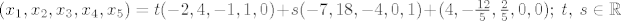
e sad. ja ne znam šta mathematica izbacuje. očito su i 'oni' uzeli da su 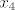 i i 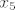 parametri. parametri.  pa se samo ispiše 'pomak'. pa se samo ispiše 'pomak'.
uglavnom, jako nam je slično 
postoji rješavač koji, doduše, nisam koristio, ali možda će biti od pomoći 
_________________
ima let u finish
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:50 uto, 12. 2. 2008 Naslov: Postano: 23:50 uto, 12. 2. 2008 Naslov: |
    |
|
|
Jasno, no kako ide "algoritam" rješavanja?
Naime, zaboravih, a nemam to sa vježbi.
Se svodi na donju trokutastu, ili kako?
Kad se svede, kud sa ostatkom?
Jasno, no kako ide "algoritam" rješavanja?
Naime, zaboravih, a nemam to sa vježbi.
Se svodi na donju trokutastu, ili kako?
Kad se svede, kud sa ostatkom?
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 12:39 sri, 13. 2. 2008 Naslov: Postano: 12:39 sri, 13. 2. 2008 Naslov: |
    |
|
|
[quote="ma"]ja sam dobio sljedeće:
[latex](x_1,x_2,x_3,x_4,x_5)=t(-2,4,-1,1,0)+s(-7,18,-4,0,1)+(4,-\frac{12}{5},\frac{2}{5},0,0); \ t, \ s\in\mathbb{R}[/latex]
e sad. ja ne znam šta mathematica izbacuje. očito su i 'oni' uzeli da su [latex]x_4[/latex] i [latex]x_5[/latex] parametri. :? pa se samo ispiše 'pomak'.
uglavnom, jako nam je slično :D
postoji [url=http://wims.unice.fr/wims/wims.cgi?module=tool/linear/linsolver.en]rješavač[/url] koji, doduše, nisam koristio, ali možda će biti od pomoći 8)[/quote]
Evo, probah taj rješavač, i evo rezultata:
This system has infinitely many solutions, which are (with parameters ri):
{ x1 = r1, x2 = -(44 r2+92 r1-284)/35, x3 = (9 r2+22 r1-74)/35, x4 = r2, x5 = (2 r2+ r1-4)/7 }.
[quote="ma"]pa želiš pojednostaviti jednadžbe i kad vidiš da je to najjednostavnije, uvedeš parametre.
nema tu gornjetrokutastih matrica...[/quote]
Ma dobro, ali što mi je ~cilj~ dobiti?
Ja sada imam:
[latex]\begin{bmatrix}
1&1&1&-1&7&|&2\\
0&2&7&-1&7&|&-2\\
0&0&5&5&21&|&2\end{bmatrix}[/latex]
| ma (napisa): | ja sam dobio sljedeće:
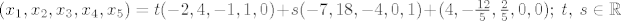
e sad. ja ne znam šta mathematica izbacuje. očito su i 'oni' uzeli da su 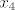 i i 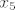 parametri. parametri.  pa se samo ispiše 'pomak'. pa se samo ispiše 'pomak'.
uglavnom, jako nam je slično 
postoji rješavač koji, doduše, nisam koristio, ali možda će biti od pomoći  |
Evo, probah taj rješavač, i evo rezultata:
This system has infinitely many solutions, which are (with parameters ri):
{ x1 = r1, x2 = -(44 r2+92 r1-284)/35, x3 = (9 r2+22 r1-74)/35, x4 = r2, x5 = (2 r2+ r1-4)/7 }.
| ma (napisa): | pa želiš pojednostaviti jednadžbe i kad vidiš da je to najjednostavnije, uvedeš parametre.
nema tu gornjetrokutastih matrica... |
Ma dobro, ali što mi je ~cilj~ dobiti?
Ja sada imam:
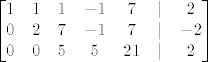
|
|
| [Vrh] |
|
|




















